лабы / бих_лр4
.docxФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
«Санкт-Петербургский государственный университет телекоммуникаций
им. проф. М. А. Бонч-Бруевича»
_____________________________________________________________________________
Кафедра радиосистем и обработки сигналов
Дисциплина «Цифровая обработка сигналов»
Лабораторная работа ЛР04
СИНТЕЗ И АНАЛИЗ БИХ-ФИЛЬТРОВ
Выполнил:
Проверил:
Санкт-Петербург
2023
Таблицы исходных данных для своего
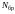 .
.
Таблица 4.1. Типы избирательности БИХ-фильтра
бригады |
Тип избирательности БИХ-фильтра |
Четный |
ФНЧ |
Нечетный |
ФВЧ |
Таблица 4.2. Требования к характеристике затухания ФВЧ
Частоты (Гц) и их идентификаторы |
Допустимые отклонения характеристики затухания (дБ) |
||||
Граничная частота ПЗ |
|
|
В ПЗ |
|
40 |
Граничная частота ПП |
|
|
В ПЗ |
|
0.4455 |
2 .
Выполнение работы.
.
Выполнение работы.
БИХ-фильтр описывается передаточной функцией общего вида:
и при (N-1)≤(M-1) (по умолчанию) имеет порядок R, равный R = (M-1).
Фильтр Баттерворта
АЧХ
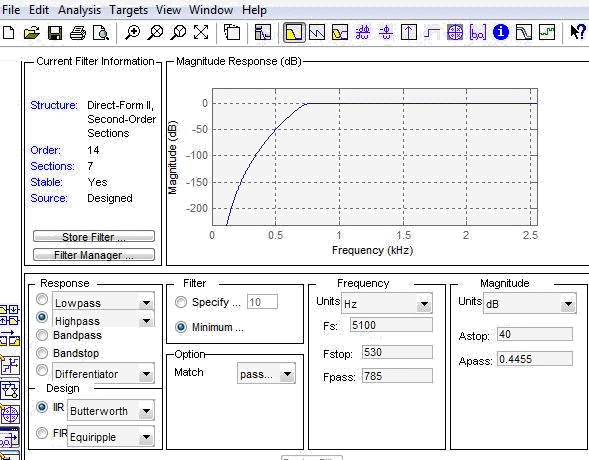
с АЧХ, максимально плоской в ПП и монотонной в ПЗ;
ФЧХ
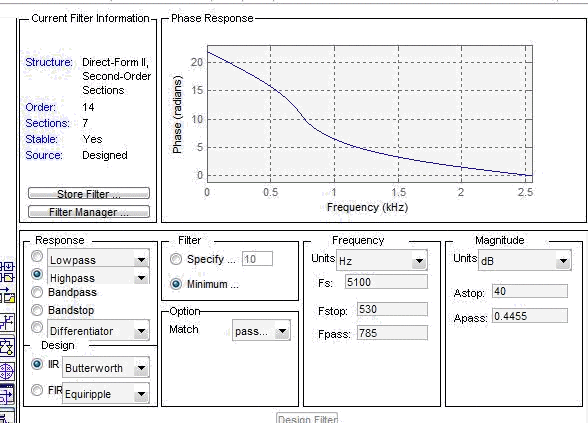
ИХ ФВЧ фильтра
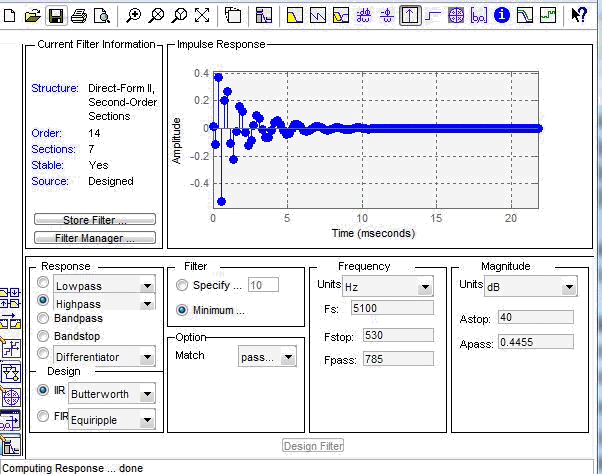
Карта нулей и полюсов:
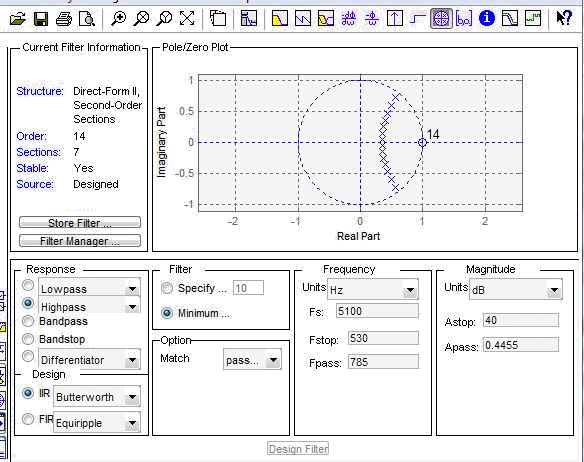
Система устойчива т.к полюса находятся в единичной окружности.
Фильтр Чебышева I рода
АЧХ
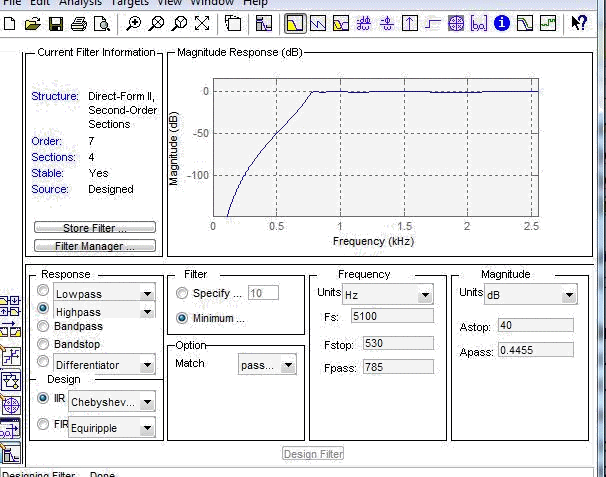
АЧХ равноволновая в ПП и монотонная в ПЗ
ФЧХ
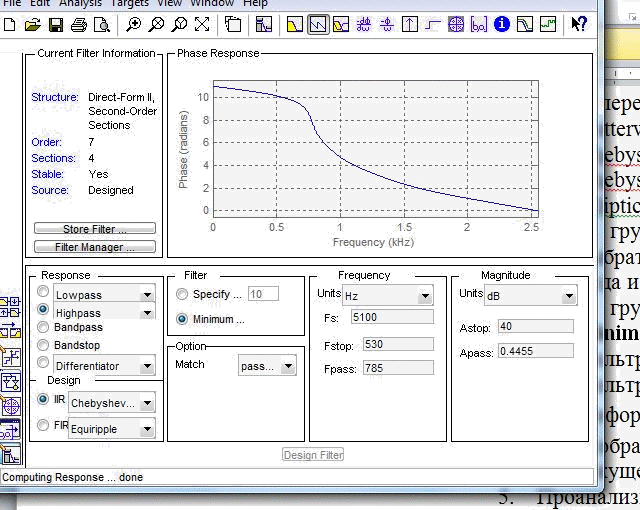
ИХ ФВЧ фильтра
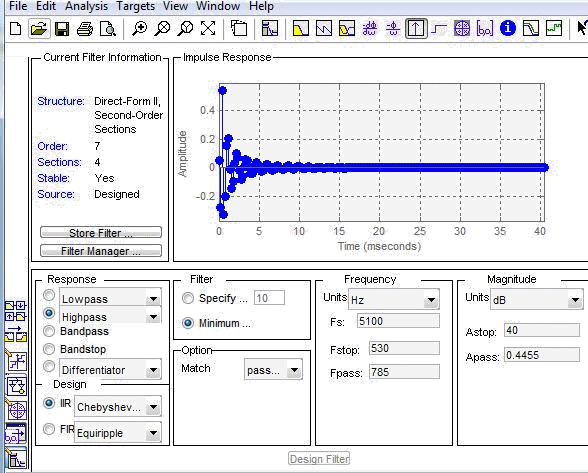
Карта нулей и полюсов:
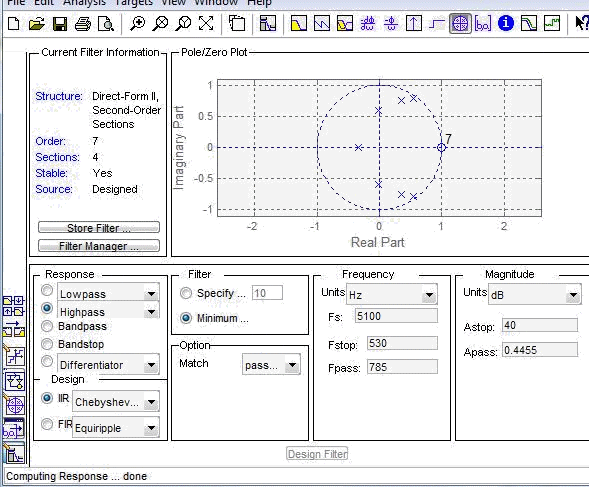
Система устойчива т.к полюса находятся в единичной окружности.
Фильтр Чебышева II рода
АЧХ
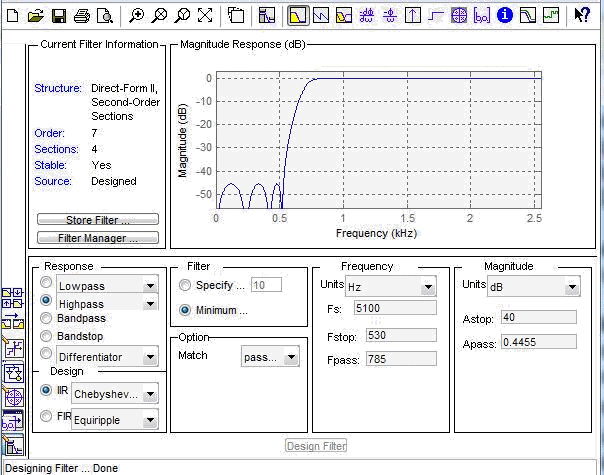
АЧХ, максимально плоской в ПП и равноволновой в ПЗ;
ФЧХ
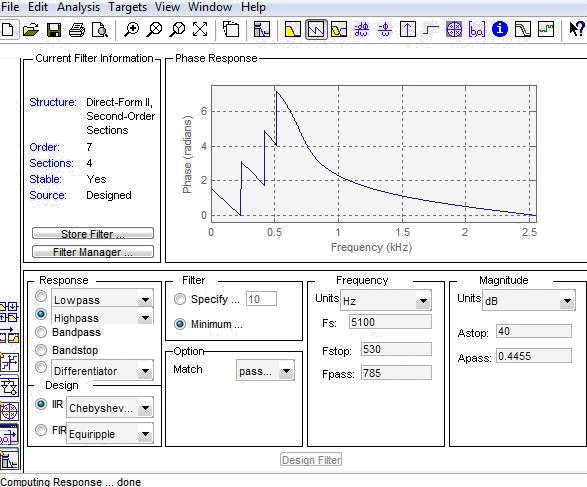
ИХ ФВЧ фильтра
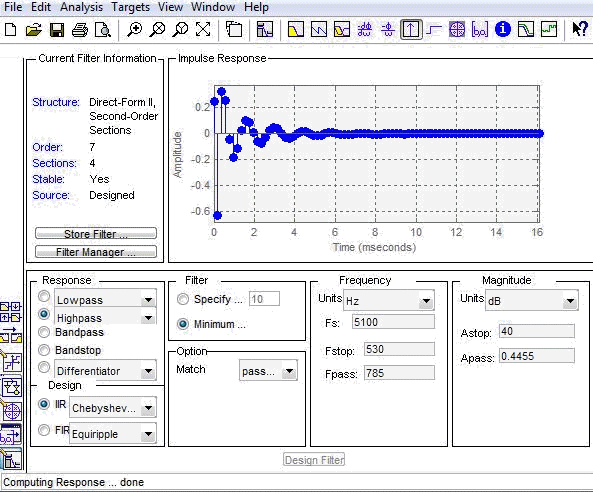
Карта нулей и полюсов:
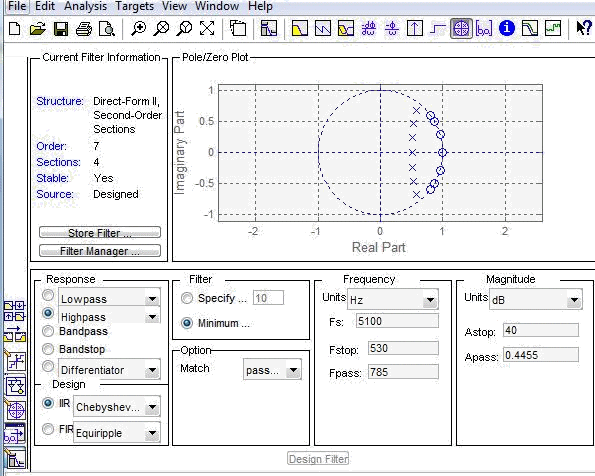
Система устойчива т.к полюса находятся в единичной окружности.
Фильтр Золотарева-Кауэра
АЧХ
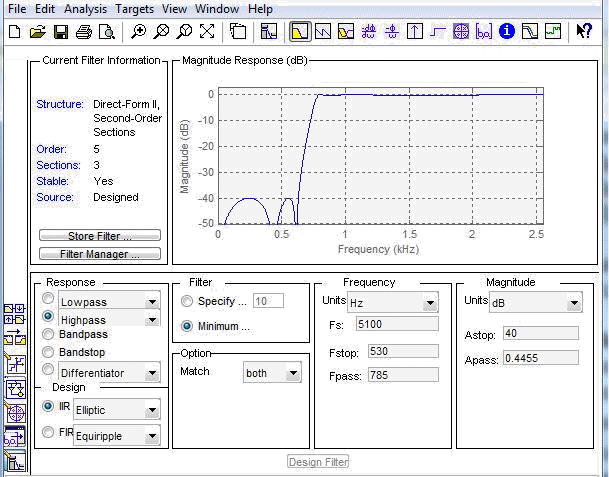
АЧХ, равноволновой в ПП и ПЗ.
ФЧХ
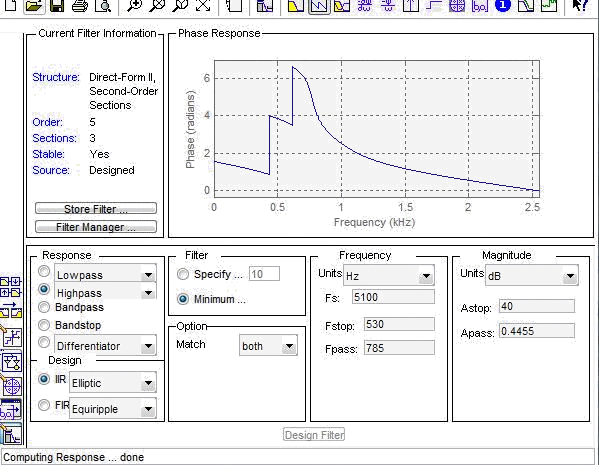
ИХ ФВЧ фильтра
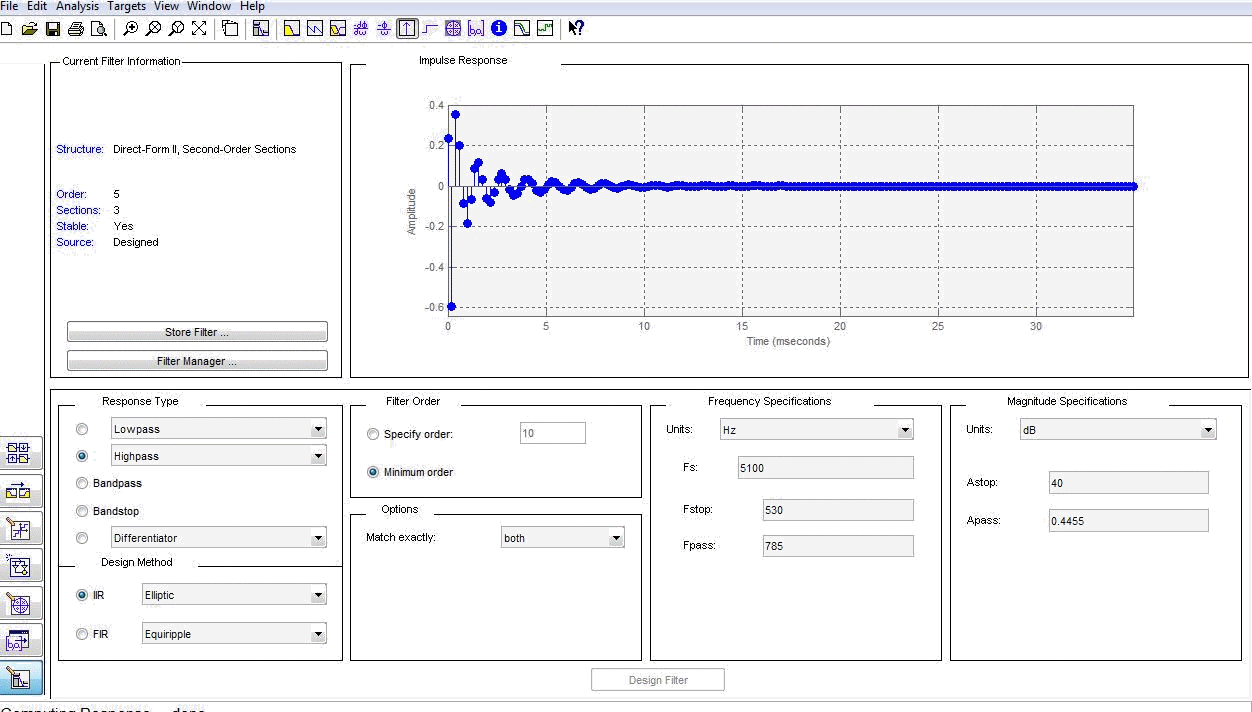
Карта нулей и полюсов:
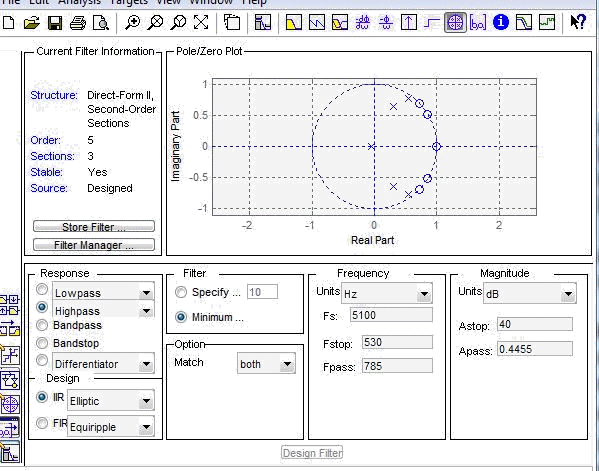
Система устойчива т.к полюса находятся в единичной окружности.
Пояснения:
Какая функция используется для вычисления порядка и частот среза:
Butterworth — фильтр Баттерворта;
Chebyshev Type I — фильтр Чебышева I рода;
Chebyshev Type II — фильтр Чебышева II рода;
Elliptic — фильтр Золотарева—Кауэра (эллиптический).
Какие функции используются для синтеза БИХ-фильров Баттерворда, Чебышева 1-го и 2-го рода и Золотарева-Кауэра

Какой из БИХ-фильтров имеет минимальный порядок:
Минимальный порядок имеет Фильтр Золотарева-Кауэра

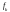
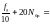 590
590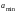
 855
855