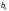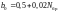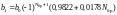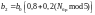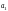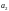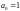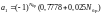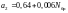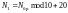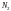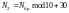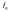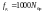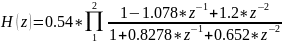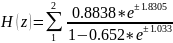Добавил:

naklpakl Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

Цифровая обработка сигналов

Файл:

лабы / 8_лаба_8.docx

Скачиваний:

Добавлен:

28.04.2023

Размер:

259.33 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Федеральное государственное образовательное бюджетное учреждение

высшего профессионального образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

_____________________________________________________________________________

Кафедра цифровой обработки сигналов

Дисциплина «Цифровая обработка сигналов»

Лабораторная работа № 8

ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ

Выполнил:

Проверил:

Санкт-Петербург

2023

Таблица исходных данных.

Переменная	Назначение	Значение	Идентификатор
	Номер бригады		Nb = 7
	Коэффициенты числителя передаточной функции		Вектор b = [0.64 -0.7083 0.768]
	Коэффициенты знаменателя передаточной функции		Вектор a = [1 -0.9528 0.682]
	Длина ИХ		N1 = 27
	Длина воздействия		N2 = 37
	Частота дискретизации		Fs = 7000

Выполнение работы

Вычисление импульсной характеристики – функция impz

disp('% п.1. ЦИФРОВОЙ ЕДИНИЧНЫЙ ИМПУЛЬС')

disp('% п.1. ВЫЧИСЛЕНИЕ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ - функция impz')

disp('%')

disp('% Для вывода ГРАФИКА ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ нажмите <ENTER>')

pause

h1 = impz(b,a,N1); % ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА

n = 0:(N1-1); % ДИСКРЕТНОЕ НОРМИРОВАННОЕ ВРЕМЯ ДЛЯ ИХ

figure('Name','Impulse Response','NumberTitle', 'off')

subplot(2,1,1), stem(n,h1,'fill','MarkerSize',3), grid

xlabel('n'), ylabel('h(n)')

title('Impulse Response h(n) - impz')

disp('%')

disp('% Для продолжения нажмите <ENTER>')

pause

disp('%')

Пояснение:

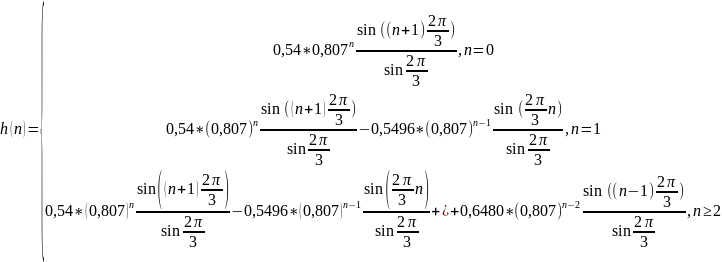
В действительности длина ИХ рекурсивных ЛДС бесконечна.

Вычисление импульсной характеристики – функция filter

disp('% п.2. ВЫЧИСЛЕНИЕ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ - функция filter')

disp('%')

disp('% Для вывода ГРАФИКА ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ нажмите <ENTER>')

pause

u0 = [1 zeros(1,(N1-1))]; % ЦИФРОВОЙ ЕДИНИЧНЫЙ ИМПУЛЬС

h2 = filter(b,a,u0); % ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА

subplot(2,1,2), stem(n,h2,'fill','MarkerSize',3), grid

xlabel('n'), ylabel('h(n)'), title('Impulse Response h(n) - filter')

disp('%')

disp('% Для продолжения нажмите <ENTER>')

pause

disp('%')

Пояснение:

В качестве воздействия выбран цифровой единичный импульс длины N₁-1, так как ИХ – это реакция на цифровой единичный импульс. Длина цифрового единичного импульса ограничивает ИХ, так как длина ИХ рекурсивной ЛДС бесконечна.

Вычисление реакции по формуле свертки

disp('% п.3. ВЫЧИСЛЕНИЕ РЕАКЦИИ ПО ФОРМУЛЕ СВЕРТКИ')

disp('%')

disp('% Для вывода ГРАФИКОВ ВОЗДЕЙСТВИЯ И РЕАКЦИИ, вычисленной по ФОРМУЛЕ СВЕРТКИ, нажмите <ENTER>')

pause

x = input_1(N2); % ВОЗДЕЙСТВИЕ (ДИСКРЕТНЫЙ ПРЯМОУГОЛЬНЫЙ ИМПУЛЬС)

y1 = conv(x,h1); % РЕАКЦИЯ ДЛИНЫ, РАВНОЙ ДЛИНЕ СВЕРТКИ

L = N1+N2-1; % ДЛИНА СВЕРТКИ

n = 0:(N2-1); % ДИСКРЕТНОЕ НОРМИРОВАННОЕ ВРЕМЯ ДЛЯ ВОЗДЕЙСТВИЯ

n1 = 0:(L-1); % ДИСКРЕТНОЕ НОРМИРОВАННОЕ ВРЕМЯ ДЛЯ СВЕРТКИ

figure('Name','Input and Output Signals','NumberTitle', 'off')

subplot(4,1,1), stem(n,x,'fill','MarkerSize',3), grid, xlabel('n')

ylabel('x(n)'), title('Input Signal - Discrete Rectangular Impulse x(n)')

subplot(4,1,2), stem(n1,y1,'fill','MarkerSize',3), grid

ylabel('y(n)'), title('Output Signal y1(n) – conv (length = L)')

subplot(4,1,3), stem(n,y1(1:N2),'fill','MarkerSize',3), grid

xlabel('n'), ylabel('y1(n)')

title('Output Signal y1(n) – conv (length = N2)')

disp('%')

disp('% Для продолжения нажмите <ENTER>')

pause

disp('%')

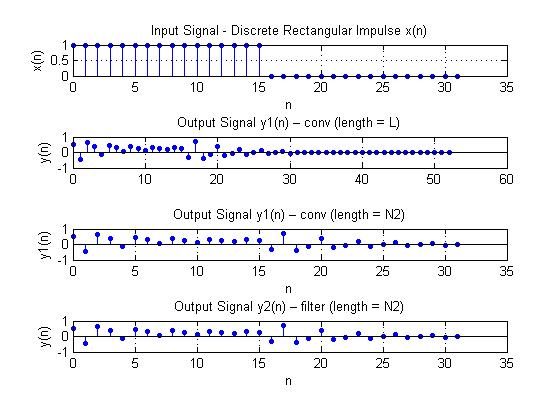
Пояснение:

Длина импульса равна int(N2/2), в данном случае 16.
Аналитически (L=N2+N1-1) и по графику (см. график) длина графика равна 53.
Ее ограничивают до длины воздействия, так как при значениях больше этой длины свертка равна нулю.

Вычисление реакции по разностному уравнению

disp('% п.4. ВЫЧИСЛЕНИЕ РЕАКЦИИ ПО РАЗНОСТНОМУ УРАВНЕНИЮ')

disp('%')

disp('% Для вывода ГРАФИКА РЕАКЦИИ, вычисленной по РАЗНОСТНОМУ УРАВНЕНИЮ, нажмите <ENTER>')

pause

y2 = filter(b,a,x); % РЕАКЦИЯ ЛДС

subplot(4,1,4), stem(n,y2,'fill','MarkerSize',3), grid

xlabel('n'), ylabel('y(n)')

title('Output Signal y2(n) – filter (length = N2)')

disp('%')

disp('% Для продолжения нажмите <ENTER>')

pause

disp('%')

Пояснение:

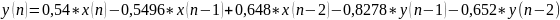
Длина реакции ограничена длиной воздействия N2=32, так как без ограничения длина реакции бесконечна.

Вычисление параметров передаточной функции в виде произведения простейших множителей

disp('% п.5. ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ ПРОИЗВЕДЕНИЯ ПРОСТЕЙШИХ МНОЖИТЕЛЕЙ')

disp('%')

disp('%Для ВЫВОДА нулей (q) и полюсов (p) В АЛГЕБРАИЧЕСКОЙ ФОРМЕ и коэффициента усиления (K) нажмите <ENTER>')

pause

[q,p,K] = tf2zpk(b,a) % НУЛИ (q) И ПОЛЮСЫ (p) В АЛГЕБРАИЧЕСКОЙ ФОРМЕ И КОЭФФИЦИЕНТ УСИЛЕНИЯ (K)

disp('%')

disp('%Для ВЫВОДА нулей (q) в ПОКАЗАТЕЛЬНОЙ ФОРМЕ нажмите <ENTER>')

pause

disp('% rq - РАДИУСЫ, wq - АРГУМЕНТЫ нулей')

rq = abs(q) % РАДИУСЫ КОМПЛЕКСНО СОПРЯЖЕННЫХ НУЛЕЙ

wq = angle(q) % АРГУМЕНТЫ КОМПЛЕКСНО СОПРЯЖЕННЫХ НУЛЕЙ

disp('%Для ВЫВОДА полюсов (p) в ПОКАЗАТЕЛЬНОЙ ФОРМЕ нажмите <ENTER>')

pause

disp('% rp - РАДИУСЫ, wp - АРГУМЕНТЫ полюсов')

rp = abs(p) % РАДИУСЫ КОМПЛЕКСНО СОПРЯЖЕННЫХ ПОЛЮСОВ

wp = angle(p) % АРГУМЕНТЫ КОМПЛЕКСНО СОПРЯЖЕННЫХ ПОЛЮСОВ

disp('%')

disp('% Для продолжения нажмите <ENTER>')

pause

disp('%')

Пояснение:

Нули и полюсы в алгебраической форме и коэффициент усиления:

q = 0.5089 + 0.9701i

0.5089 - 0.9701i

p = -0.4139 + 0.6933i

-0.4139 - 0.6933i

K = 0.5400

Нули в показательной форме:

rq = 1.0954

1.0954

wq = 1.0877

-1.0877

Полюсы в показательной форме:

rp = 0.8075 0.8075

wp = 2.1090 -2.1090

Связь между алгебраической и показательной формами на примере нулей:

r=sqrt(0.5089²+0.970²)

w=-arctg(0.97/0.5089)

wq=0.346*π

-0.346*π

wp=0.671π

-0.671π

Вычисление параметров передаточной функции в виде произведения множителей второго порядка.

disp('% п.6. ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ ПРОИЗВЕДЕНИЯ МНОЖИТЕЛЕЙ ВТОРОГО ПОРЯДКА')

disp('%')

disp('% Для ВЫВОДА матрицы коэффициентов (s) и коэффициента усиления (G) нажмите <ENTER>')

pause

[s,G] = tf2sos(b,a) % КОЭФФИЦИЕНТЫ (s) И КОЭФФИЦИЕНТ УСИЛЕНИЯ (G)

disp('%')

disp('% Для продолжения нажмите <ENTER>')

pause

disp('%')

s = 1.0000 -1.0178 1.2000 1.0000 0.8278 0.6520

G = 0.5400

Пояснение:

Вычисление параметров передаточной функции в виде суммы простых дробей

disp('% п.7. ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СУММЫ ПРОСТЫХ ДРОБЕЙ')

disp('%')

disp('% Для ВЫВОДА коэффициентов разложения (r), полюсов (p) и целой части (c) нажмите <ENTER>')

pause

[r,p,c] = residuez(b,a) % КОЭФФИЦИНТЫ РАЗЛОЖЕНИЯ (r) и ПОЛЮСЫ (p) В АЛГЕБРАИЧЕСКОЙ ФОРМЕ И ЦЕЛАЯ ЧАСТЬ (c)

disp('%')

disp('%Для ВЫВОДА КОЭФФИЦИЕНТОВ РАЗЛОЖЕНИЯ (r) в ПОКАЗАТЕЛЬНОЙ ФОРМЕ нажмите <ENTER>')

pause

rr = abs(r) % РАДИУСЫ КОМПЛЕКСНО СОПРЯЖЕННЫХ КОЭФФИЦИЕНТОВ РАЗЛОЖЕНИЯ (r)

wr = angle(r) % АРГУМЕНТЫ КОМПЛЕКСНО СОПРЯЖЕННЫХ КОЭФФИЦИЕНТОВ РАЗЛОЖЕНИЯ (r)

disp('%')

disp('% Для продолжения нажмите <ENTER>')

pause

disp('%')

Пояснение:

Коэффициенты разложения, полюсов и целой части:

r = -0.2269 + 0.8542i

-0.2269 - 0.8542i

p = -0.4139 + 0.6933i

-0.4139 - 0.6933i

c = 0.9939

Коэффициенты разложения в показательной форме:

rr = 0.8838

0.8838

wr = 1.8305

-1.8305

rp= 0.6520

0.6520

wp= 1.033

-1.033

wr=0.583*π

wp=0.329*π

Вывод карты нулей и полюсов.

disp('% п.8. ВЫВОД КАРТЫ НУЛЕЙ И ПОЛЮСОВ')

disp('%')

disp('% Для ВЫВОДА КАРТЫ НУЛЕЙ И ПОЛЮСОВ нажмите <ENTER>')

pause

figure('Name',' Z-plane zero-pole plot','NumberTitle', 'off')

zplane(b,a), title('Z-plane zero-pole plot'), grid

xlabel('Re'), ylabel('jIm')

disp('%')

disp('% Для продолжения нажмите <ENTER>')

pause

disp('%')

Пояснение:

Рекурсивное звено является устойчивым, так как все полюса лежат внутри единичного круга (по второму критерию устойчивости).

Значения нулей и полюсов совпадают с вычисленными в пункте 5.

Вычисление АЧХ и ФЧХ в шкале нормированных частот.

disp('% п.9.ВЫЧИСЛЕНИЕ АЧХ и ФЧХ В ШКАЛЕ НОРМИРОВАННЫХ ЧАСТОТ')

disp('%')

disp('% Для вывода ГРАФИКОВ АЧХ и ФЧХ с шкале НОРМИРОВАННЫХ частот нажмите <ENTER>')

pause

w = 0:pi/100:pi; % ВЕКТОР НОРМИРОВАННЫХ ЧАСТОТ (РАД)

H_w = freqz(b,a,w); % КОМПЛЕКСНАЯ ЧАСТОТНАЯ ХАРАКТЕРИСТИКА

MAG_w = abs(H_w); % АЧХ

PHASE_w = angle(H_w); % ФЧХ

figure('Name','Magnitude and Phase Responses','NumberTitle', 'off')

subplot(2,2,1), plot(w,MAG_w), grid, xlabel('w (rad)'), title('MAGNITUDE - |Н(w)|')

subplot(2,2,3), plot(w,PHASE_w), grid, xlabel('w (rad)'), title('PHASE – arg [H(w)] (rad)')

disp('%')

disp('% Для продолжения нажмите <ENTER>')

pause

disp('%')

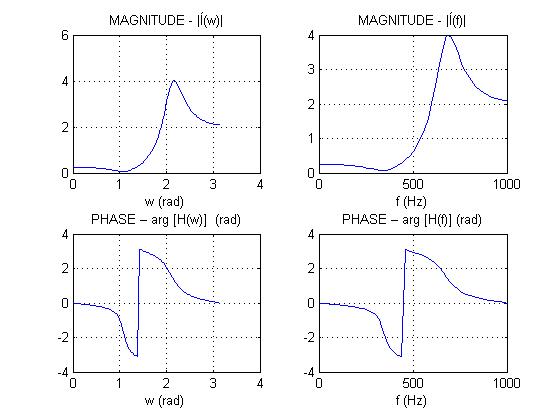
Пояснение:

Границы основной полосы частот [0;π].
Вид АЧХ соответствует карте нулей и полюсов, так как на частоте комплексно-сопряженных нулей и полюсов мы наблюдаем минимум и максимум соответственно.
В реакции оказались преимущественно подавлены высокие частотные составляющие.

1 / 21 2 > Следующая >>>

Соседние файлы в папке лабы

#
28.04.2023531.33 Кб227_лаба_7.docx
#
28.04.2023259.33 Кб168_лаба_8.docx
#
28.04.20231.31 Mб11бих_лр4.docx
#
28.04.20231.51 Mб11ких_7_лр3.doc