
pokazateli_variatsii
.doc
Текст лекции
Тема: «Показатели вариации»
(лекция – 1,0 ч.)
Для студентов всех специальностей
|
План лекции |
стр. |
|
1. Понятие вариации и показатели ее размера
|
3 |
|
2. Дисперсия альтернативного признака
|
5 5 6 |
|
Контрольные вопросы |
7 |
|
Список использованной литературы |
7 |
-
Понятие вариации и показатели ее размера
Любая статистическая совокупность состоит из единиц, значения признака которых варьируют. Для того, чтобы судить об однородности совокупности и типичности средней величины изучаемого признака анализ следует дополнять исчислением показателей вариации.
Вариация – это колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности.
Показатели вариации бывают:
1. Абсолютные показатели:
1)размах вариации;
2)среднее линейное отклонение;
3)дисперсия;
4)среднее квадратическое отклонение.
2. Относительные показатели:
1)коэффициент вариации,
2)коэффициент осцилляции;
3)линейный коэффициент вариации.
Подробнее о показателях вариации:
-
Размах вариации
Характеризует границы вариации изучаемого признака и определяется по формуле:
R = Хmax – Xmin,
где
Xmax – максимальное значение варьирующего признака;
Xmin – минимальное значение варьирующего признака.
Размах показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака. Он основан на крайних значениях варьирующего признака и не отражает отклонений всех вариант в ряду
-
Дисперсия
Средний квадрат отклонений индивидуальных значений признака от их средней величины. Она вычисляется по формулам:
1 способ определения дисперсии
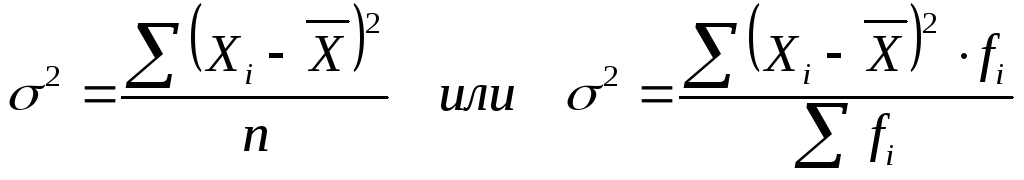 ,
,
где
Хi – индивидуальные значения варьирующего признака (варианты);
![]() -
среднее значение варьирующего признака;
-
среднее значение варьирующего признака;
n- количество разновидностей вариант;
fi - показатель повторяемости вариант (частоты, веса);
2 способ определения дисперсии
![]() ,
,
где
![]() -
средняя из квадратов индивидуальных
значений;
-
средняя из квадратов индивидуальных
значений;
![]() -
квадрат средней величины признака;
-
квадрат средней величины признака;
3 способ определения дисперсии – метод моментов
![]() ,
,
где
![]() -
величина интервала в интервальном ряду;
-
величина интервала в интервальном ряду;
![]() -
момент первого порядка;
-
момент первого порядка;
![]() -
момент второго порядка, который
определяется по формуле
-
момент второго порядка, который
определяется по формуле
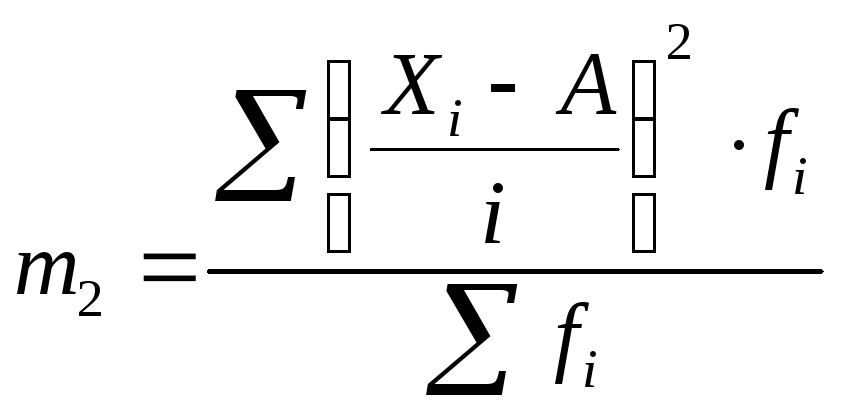
-
Среднее квадратическое отклонение
Обобщающая характеристика размеров вариации признака в совокупности определяется по формуле:
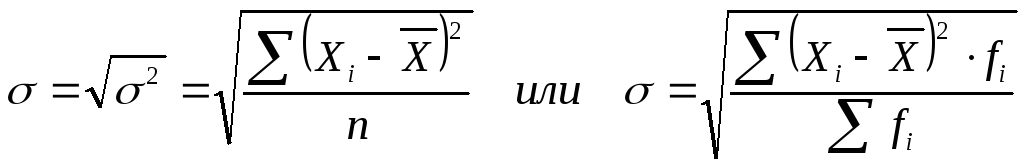
Среднее квадратическое отклонение показывает, на сколько в среднем значение признака отличается от стандартного значения и выражается в тех же единицах измерения, что и признак.
-
Среднее линейное отклонение
![]()
Среднее линейное отклонение характеризует. на сколько отклоняется признак в изучаемой совокупности от средней величины признака.
Этот показатель рассчитывается по модулю.
-
Коэффициент вариации
![]()
Этот показатель характеризует меру вариации значений признака вокруг средней величины.
Чем этот показатель меньше, тем однороднее совокупность, а средняя величина признака типична для данной совокупности. Чем коэффициент вариации больше, тем неоднороднее совокупность.
-
Линейный коэффициент вариации
![]()
-
Коэффициент осцилляции
![]()
Техника вычисления дисперсии может быть упрощена, если использовать ряд её математических свойств.
Математические свойства дисперсии:
-
Если из всех значений вариант отнять какое-то постоянное число А, то средний квадрат отклонений от этого не изменится
![]()
-
Если все значения вариант разделить на какое-то постоянное число А, то средний квадрат отклонений уменьшится от этого в А2 раз, а среднее квадратическое отклонение - в А раз
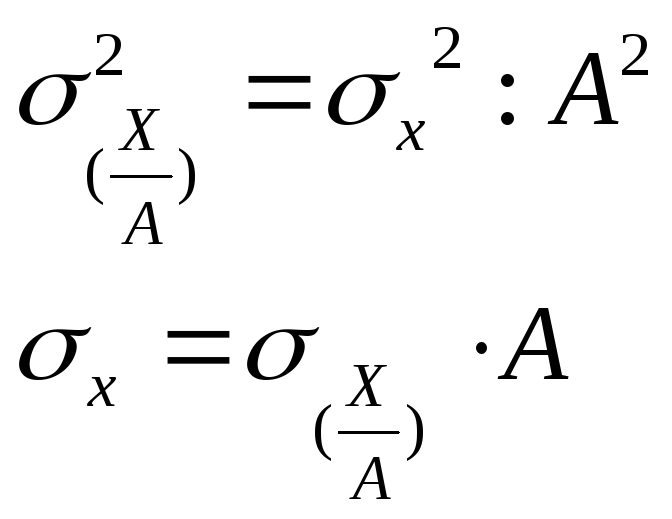
-
Если исчислить средний квадрат отклонений от любой величины (А), в той или иной степени отличающейся от средней арифметической (
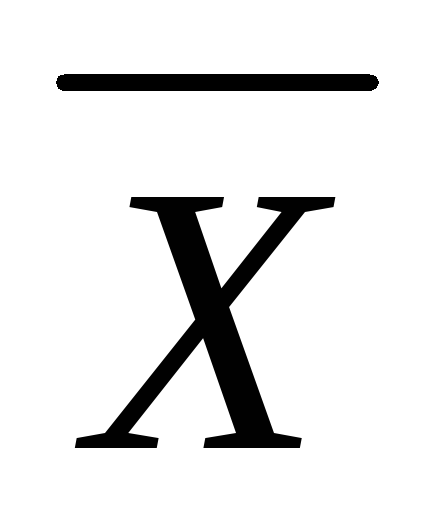 ),
то он всегда будет больше среднего
квадрата отклонений, исчисленного от
средней арифметической
),
то он всегда будет больше среднего
квадрата отклонений, исчисленного от
средней арифметической
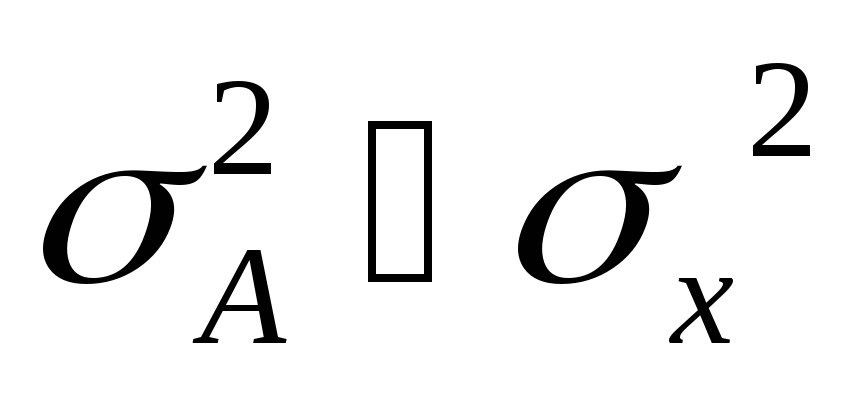
Свойство минимальности:
Дисперсия средней всегда меньше дисперсий, исчисленных от любых других величин.
-
Дисперсия альтернативного признака
Среди множества признаков, изучаемых статистикой, выделяют такие, которыми обладают одни единицы совокупности и не обладают другие, называемые альтернативными.
Альтернативный признак – это признак, которым обладают одни единицы и не обладают другие единицы совокупности.
Вариация альтернативного признака количественно проявляется в значении нуля у единиц, которые этим признаком не обладают, или единицы у тех, которые данный признак имеют.
Средняя и дисперсия альтернативного признака делятся на:
-
Среднее значение альтернативного признака
![]() ,
,
так
как
![]()
-
Дисперсия альтернативного признака
![]()
где
р – доля единиц, обладающих признаком, в численности всей совокупности;
q- доля единиц совокупности, не обладающих этим признаком (q=1-р).
-
Закон сложения (разложения) вариации (дисперсии)
Вариация признака обусловлена различными факторами. Выделить влияние некоторых факторов можно, если разбить статистическую совокупность на группы. Это даёт возможность изучить вариацию признака по всей совокупности в целом, а также вариацию для каждой группы и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсий.
Закон сложения (разложения) дисперсий
Общая
дисперсия σ2
= δ2
+
![]() ,
характеризует вариацию признака во
всей совокупности под влиянием всех
факторов, обусловивших эту вариацию.
,
характеризует вариацию признака во
всей совокупности под влиянием всех
факторов, обусловивших эту вариацию.
Где:
-
Межгрупповая дисперсия (δ2)
Характеризует вариацию изучаемого признака под влиянием признака-фактора, положенного в основание группировки.
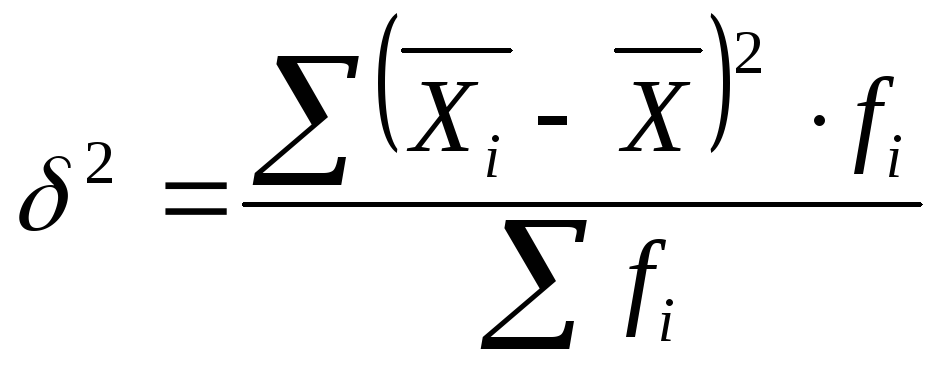
где
![]() -
общая средняя;
-
общая средняя;
![]() -
средняя i- группы;
-
средняя i- группы;
![]() -
частота i- группы.
-
частота i- группы.
-
Средняя из внутригрупповых дисперсий (
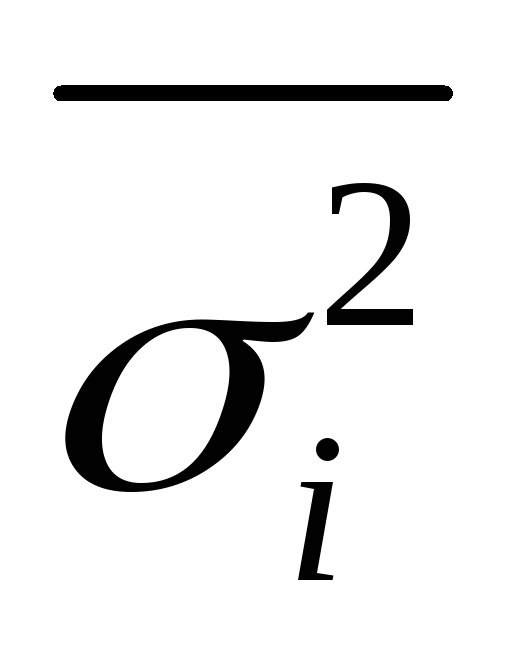 )
)
Отражает случайную вариацию обусловленную неучтенными факторами и не зависящую от признака-фактора, положенного в основание группировки
![]() ,
,
где
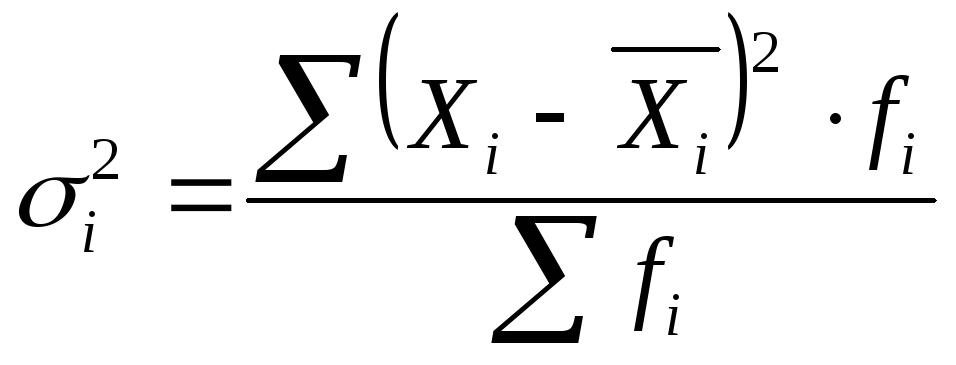 -
внутригрупповая дисперсия i- группы
-
внутригрупповая дисперсия i- группы
Различные виды дисперсий широко используют для исчисления показателей тесноты связи между признаками.
-
Коэффициент детерминации, эмпирическое корреляционное отношение
Эмпирическое корреляционное отношение
Изменяется в пределах [0,1]
![]()
Характеризует влияние признака, положенного в основание группировки. Если η =0, то группировочный признак не оказывает влияния на результативный. Если η=1, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю.
Эмпирическое корреляционное отношение может быть только положительным. Качественная интерпретация показателя осуществляется посредством шкалы Чэддока.
Шкала значений эмпирического корреляционного отношения
Категория |
Границы значений эмпирического корреляционного отношения |
|
Связь очень слабая |
0,1 – 0,3 |
|
Умеренная |
0,3 – 0,5 |
|
Заметная |
0,5 – 0,7 |
|
Тесная |
0,7-0,9 |
|
Весьма тесная |
0,9-0,99 |
На основе эмпирического корреляционного отношения рассчитывают коэффициент детерминации.
Эмпирический коэффициент детерминации
![]()
Показывает долю (удельный вес) общей вариации изучаемого признака, обусловленную вариацией группировочного признака.
Контрольные вопросы для самоподготовки:
-
Виды вариационных рядов. Абсолютные показатели размера вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
-
Относительные показатели вариации: коэффициент вариации, коэффициент осцилляции.
-
Дисперсия альтернативного признака. Математические свойства дисперсии.
-
Закон сложения (разложения) вариации и дисперсии. Применение дисперсии для оценки степени взаимосвязей в группировках и социально – экономических явлениях
Список литературы
Базовый учебник
-
Статистика: Учебно-практич. пособие / Под. ред. М.Г. Назарова.- М.:КНОРУС,2006*;
-
Социально-экономическая статистика. Практикум / под ред. С.А. Орехова. – М.: Эксмо, 2007. – 384 с.*
Основная литература
1. Теория статистики: Учебник / Под ред. Р.А. Шмойловой.-5-е изд.- М.: Финансы и статистика, 2005;*
-
Практикум по теории статистики. Учебное пособие. /Под ред. Шмойловой Р.А. - М.: Финансы и статистика, 2002*;
-
Статистика финансов: Учеб. Пособие / под ред.М.Г. Назарова. – М: Омега-Л, 2005. – 380 с.*
-
Статистика: Учебник / Под ред. В.Г. Ионина.-3-е изд., перераб. и доп.-М.: ИНФРА-М, 2006*
Дополнительная литература
1. Статистика: Учебник / Под ред. И.И. Елисеевой.-М.: Высшее образование, 2006*;
2. Гусаров В.М. Статистика: Учеб. пособие для вузов. - М: ЮНИТИ-ДАНА, 2001*;
3. Статистика: Учебник / Под ред. B.C. Мхитаряна.-М.: Экономистъ, 2005*;
4. Статистика: Учеб.пособие / Под ред. В.М. Симчеры.- М.: Финансы и статистика, 2005*;
5. Салин В.Н., Чурилова Э.Ю. Курс теории статистики для подготовки специалистов финансово-экономического профиля: Учебник. - М.: Финансы и статистика, 2006*;
6. Журнал «Вопросы статистики».
