
MAIN
.pdf1Список вопросов
1.Понятие алгоритмов. Задачи и языки.
2.Алфавит. Слово. Множество всех слов. Свойства: X , конкатенация.
3.Множество X - счетно.
4.Теорема о несчетности множества всех языков.
5.КДА. Способы задания.
6.Распознавание слов и языка КДА. Примеры языков.
7.Класс языков Reg. Теорема о счетности множества Reg. Следствие - существуют нерегулярные языки.
8.Множество всех языков с операцией объединения - коммутатисная полугруппа. Множество языков с объединением и конкатенацией - полукольцо.
9.dim(L) - размерность регулрного языка. Проблема нахождения минимального автомата.
10.Конечный язык. Его регулярность. Размерность конечного языка.
11.Пересечение, объединение, дополнение регулярных языков - тоже регулярный язык.
12.Объединение и пересечение конечного числа регулярных языков - регулрно.
13.Проблема регулярности счетного объединения регулярных языков.
14.Булевы функции и языки. Примеры КДА для булевых функций.
15.БДА. Свободный БДА. Произвольный язык L распознается БДА.
16.Отношение L-эквивалентности. 2 определения.
17.Rang(L). Ранг произвольного языка.
18.Теорема Майхилла - Нероуда. 1 часть.
1

19.Теорема Майхилла - Нероуда. 2 часть.
20.Следствие теоремы Майхилла - Нероуда: dim(L) = Rang(L).
21.Применение теоремы Майхилла - Нероуда. Примеры регулярных языков.
22.Построение минимального КДА для регулярного языка на основе критерия Майхилла - Нероуда.
23.EQ2n+1, EQ2n+1, O2n, O02n - оценки размерности сверху/снизу.
24.Линейное представление автомата. Конечный автомат - программистский подход. Задача - решение - представление.
25.КНА - представление слова, представление языка.
26.Класс NReg.
27.NReg = Reg.
28.Ndim(L) è dim(L).
29.Ndim(EQ2n+1).
30.Ndim(EQ2n+1)
31.Объединение регулярных языков - регулярно (доказательство с использованием КНА).
32.Конкатенация регулярных языков - регулярна (доказательство с использованием КНА).
33.Итерация регулярных языков - регулярна (доказательство с использованием КНА).
2
2Ответы
Вопрос 1,2,3,4
1, 2, 3
X = fx1; x2; : : : ; xng алфавит X = f0; 1g xi - буква
Умножение букв = приписывание
01 - слово
X = fw : w - слово в алфавите Xg - мнв всех слов конечной длины
010011. . . - сверхслово
X+ = f0; 1; 00; 01; 10; 11; 000; : : : ; 111; : : : ; 00 : : : 0; : : : ; 11 : : : 1g
|{z}
n
jX+j = 2 + 22 + 23 + + 2n
Свойство 1. kX k - счетно.
Доказательство. Нужно указать процедуру нумерации. Пусть X = f0; 1g; f0; 1g
0 ; |
1 |
; 01 ; 10 ; |
11 |
; 000 ; 001 ; : : : |
|
||
|{z}1 |
|{z}2 |
|{z}3 |
|{z}4 |
|{z}5 |
|{z}6 |
|{z}7 |
|
Свойство 2. < X ; > - полугруппа с конкатенацией и нейтральным элементом. Некоммутативная.
Определение 1. Язык - это произвольное подмножество множества X . (L X )
Пример 1. X = f0; 1g
1.L = f0g
2.L = f0; 1g
3.L = X
4.L = f00; 0000; : : : g
X = fкириллица, tg
L = Ðß
3

Свойство 3. L = fL : L X g - несчетное.
Доказательство. От противного. Пусть L - счетное.
L = fL1; L2; : : : ; Lng |
(1) |
Нужно доказать, что некоторый язык не имеет номера. Используетя диа-
гональная конструкция.
X - счетное. Берем произвольную нумерацию X . Каждому языку L ставим в соответствии взаимнооднозначную последовательность: L () a(L) = (0; 1; 1; 1; : : : ). Для каждого языка строим эти характерестические последовательности. В результате образуется матрица:
L1 = |
0 |
0 |
1 |
1 |
: : : |
1 |
L2 = |
1 |
0 |
0 : : : |
|||
: : : |
B |
: : : |
|
|
|
C |
|
B |
|
|
|
|
C |
Ln = |
B |
n1 |
n2 |
n3 |
: : : |
C |
B |
C |
|||||
|
B |
|
|
|
|
C |
|
B |
|
|
|
|
C |
|
B |
|
|
|
|
C |
|
B |
|
|
|
|
C |
|
B |
|
|
|
|
C |
|
B |
|
|
|
|
C |
|
@ |
|
|
|
|
A |
Счетное число стрîê è ñòîëáöîâ.
L() a(L) = ( 11; 12; : : : ; nn; : : : )
L, L1; L , L2; : : : ; L , Ln; : : :
По предположению язык L имеет номер. Пусть имеет номер m, но Lm = L Это противоречит (1).
Операции: [; L [ L0
; - пустое множество, нейтральный элемент.
L [ ; = L
Коммутативный.
< L; [ > - коммутативная полугруппа.
4
Определение 2. Задача - вычислительная задача. Состоит из:
1.Исходное условие
2.Исходные данные
3.Ответ
4
Пример 2. Решить систему линейных, квадратичных уравнений. Конкретная задача:
w =код(условие)код(данные)код(ответ)
Слово соответстует задаче.
Ç ! L3 = fw : w код, соответствующий этой задаче g
Задача в наших терминах - это язык. w X
w ! |
8íåò |
w < L |
|
äà |
w 2 L |
>
>
<
>
>
:
5

Вопрос 5,6
3Конечный детерминированный автомат
Определение 3.1. Конечным детерминированным автоматом A (сокращенно КДА) называют пятерку A = hX; S; ; s0; Fi.
Здесь X конечный алфавит, S = fs1; s2; : : : ; sdg конечное множество состояний, : S X ! S функция переходов автомата A, s0 2 Sначальное состояние автомата, F S множество финальных состо-
ÿíèé.
Автомат начинает работу с начального состояния s0. Под воздействи- ем букв входного слова автомат A на каждом шаге работы изменяет свои состояния в соответствии с функцией переходов.
Способы задания КДА:
в виде таблицы табличное задание автомата;
в виде диаграммы задание автомата графом: G = hS; Vi;
матричное задание функции переходов. Такому заданию функции переходу соответствует векторно-матричное задание автомата.
Определение 3.2. Сложностью (размерностью) конечного детерминированного автомата A = hX; S; ; s0; Fi будем называть чило его состояний.
Сложность автомата A будем обозначать dim(A):
dim(A) = jSj:
4Распознавание языков
F S принимающее подмножество состояний. F = SnF отвергающее подмножество состояний.
! 2 X , ! = x1x2 : : : xn задает траекторию вычислений A на !.
S0 |
x1 |
S1 |
|
x2 |
S2 |
x3 |
: : : |
xn |
Sn |
|
|
|
|
|
|||||
Определение 4.1.n |
Слово n! ïринимается автоматом A, если Sn 2 F. Îò- |
||||||||
вергается, если S |
< F, S 2F. |
|
|
|
|
||||
6
Определение 4.2. Язык L распознается автоматом A, если все слова этого языка принимаются A:
L = f! 2 L : ! принимается Ag:
Дополнение L: L = X nL:
Свойство: Если L распознается автоматом A, то L распознается неким конечным автоматом A0.
Доказательство: Если A = hX; S; ; s0; Fi, òî A0 = hX; S; ; s0;Fi, ãäå F =
SnF.
Примеры автоматов, распознающих языки
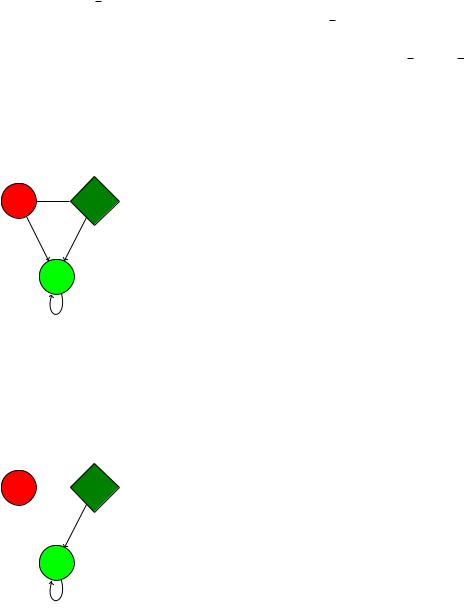
1. A: L = f0g
S0 0  S1
S1
10,1
S2
0,1
|
0 |
1 |
Í |
Ô |
|
|
|
|
|
S0 |
S1 |
S2 |
1 |
|
S1 |
S2 |
S2 |
|
1 |
S2 |
S2 |
S2 |
|
|
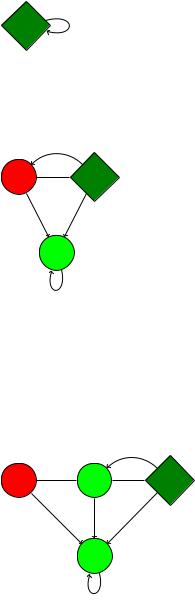
2. A: L = X = f0; 1g
0,1
S0  S1
S1
0,1
S2
0,1
7
|
|
|
0 |
1 |
Í |
Ô |
|
|
|
|
|
|
|
|
S0 |
|
S1 |
S1 |
1 |
|
|
S1 |
|
S2 |
S2 |
|
1 |
|
S2 |
|
S2 |
S2 |
|
|
3. A: L = X |
|
|
|
|||
|
S0 |
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
Í |
Ô |
|
|
|
|
|
|
|
|
S0 |
|
S0 |
S0 |
1 |
1 |
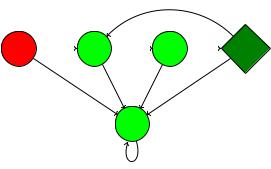
4. A: L = f0; 000; : : : - нечетныеg
0
S0 0  S1
S1
11
S2
0,1
|
0 |
1 |
Í |
Ô |
|
|
|
|
|
S0 |
S1 |
S2 |
1 |
|
S1 |
S0 |
S2 |
|
1 |
S2 |
S2 |
S2 |
|
|
5. A: L = f00; 0000; : : : - четныеg
0
S0 0  S1 0
S1 0  S2
S2
1 1 1
S3
0,1
8
|
0 |
1 |
Í |
Ô |
|
|
|
|
|
S0 |
S1 |
S3 |
1 |
|
S1 |
S2 |
S3 |
|
|
S2 |
S1 |
S3 |
|
1 |
S3 |
S3 |
S3 |
|
|
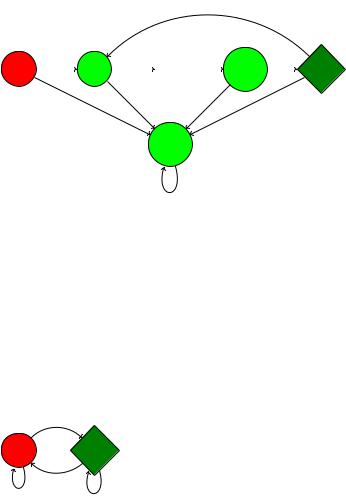
6. A: L = f000; 000000; : : : - кратно 3g 0
S0 |
0 |
|
|
S1 |
|
0 |
S2 |
0 |
S3 |
||
1 |
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
1 |
1 |
|
||
|
|
|
|
|
|
|
|
S4 |
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
1 |
|
Í |
Ô |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
S0 |
|
S1 |
S4 |
|
1 |
|
|
|
|
|
|
S1 |
|
S2 |
S4 |
|
|
|
|
|
|
|
|
S2 |
|
S3 |
S4 |
|
|
|
|
|
|
|
|
S3 |
|
S1 |
S4 |
|
|
|
1 |
|
|
|
|
S4 |
|
S4 |
S4 |
|
|
|
|
|
|
|
|
7. A: L = f0 : : : 0; 0 : : : 0; : : : - кратно kg
|{z} |{z}
k2k
9
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
S0 |
0 |
|
0 |
|
|
|
0 |
Sk 1 |
0 |
Sk |
|||
|
|
|
S1 |
|
|
|
. . . |
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
1 |
1 |
|
|
|
|
1 |
1 |
|
|
|||
|
|
|
|
|
|
|
|
Sk+1 |
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
Í |
Ô |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S0 |
|
S1 |
Sk+1 |
|
1 |
|
|
|
|
|
|
||
S1 |
|
S2 |
Sk+1 |
|
|
|
|
|
|
|
|
||
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Sk 1 |
|
Sk |
Sk+1 |
|
|
|
|
|
|
|
|
||
Sk |
|
S1 |
Sk+1 |
|
|
|
1 |
|
|
|
|
||
Sk+1 |
|
Sk+1 |
Sk+1 |
|
|
|
|
|
|
|
|
||
8. A: L = fX 1 - все, что заканчивается на 1g
1
|
S0 |
|
|
S1 |
|||
0 |
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
Í |
Ô |
|
|
S0 |
S0 |
S1 |
|
1 |
|
|
|
S1 |
S0 |
S1 |
|
|
1 |
|
9. A: L = f1X |
- все, что начинается на 1g |
||||||
10
