MAIN

11

Вопрос 7

1.Класс языков Reg.

2.Теорема:Множество всех языков,принадлежащих классу Reg счетно.

3.Следствие: множество всех языков с операцией объединения и конкатенации это полукольцо.

L-множество всех языков.

Определение 1. Класс Reg -это множество всех регулярных языков, которые распознаются автоматом.

Reg L

Теорема 1 (Reg L). Множество всех регулярных языков счетно

Доказательство: L1={0},L2={00},. . . ,Ln= {00. . . 0} - это счетная последо- вательность регулярных языков.

У счетного множества есть счетные подмножества.Надо доказать,что их не более чем счетное множество. A={A:A-KA, множество конечных

автоматов вообще}

A=<X, S, ,S0,F> выделим автоматы с конкретными параметрами A(t,d)={A:A=<X,S, ,S0,F>} |x|=t -число букв, |S|=d -число состояний. Тогда A=[A(t,d) t 0 d 0

Это значит, что множество всех букв мы можем упорядочить в виде таблицы. Т.е . конкретный КА автомат можемпредставить в виде слова в алфавите.А всех слов счетное множество. Значит A не более чем счетно.

Следствие 1. Пусть L- произвольный регулярный язык,L Reg .Верно ли, что любое подмножество языка L' L является регулярным?

L1 L2

L01={1}, L01 {L2} Ответ: это верно. А верно ли для произвольного?

Lx={L:L X*} Ответ: нет.

12

Вопрос 8

1.Свойство: множество всех языков L с операцией объединения [ - коммутативная полугруппа.

2.Свойство:множество всех языков L с операциями объединения [ и конкатенации является полукольцом с нулем Ш и еденицей {e}.

Добавим Ш - пустой язык. L [ Ш=L=Ш [ L. Операция [ - коммутативна.

Свойство 1. < L,[> -коммутативная полугруппа.

Свойство 2. Множество всех языков L с операциями объединения [ и конкатенации является полукольцом с нулем Ш и еденицей {e}.

13

Вопрос 9,10

Конечные языки

Пусть x = fX1; : : : ; Xtg алфавит.

L X

Определение 4.1. Язык L называется конечным, если jLj < 1 (т. е. число слов в нем конечно).

Теорема 4.1. Пусть L конечный язык. Тогда L регулярный язык. (L 2 Reg)

Доказательство. Пусть jLj = k, и язык L представляет конечный набор

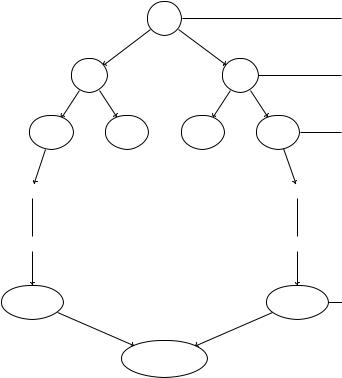
ñëîâ L = fW1; W2; : : : ; Wkg. Через l обозначим максимальную из длин: l = max fjW1j; jW2j; : : : ; jWkjg. Необходимо построить диаграмму конечного автомата: A = hX; S; ; S0; Fi. Построим ее в виде l ярусного дерева. На нулевом ярусе находится начальное состояние Se. Из состояния Se âû- ходят t дуг с надписями X1; X2; : : : ; Xt в различные состояния первого уровня. Из каждого состояния первого уровня выходят t дуг с надпи-

ñÿìè X1; X2; : : : ; Xt в свои различные состояния второго уровня так, что во втором уровне имеется ровно t2 состояний. Из каждого второго уров-

ня t дуг с надписями X1; X2; : : : ; Xt в свои различные состояния третьего уровня, так что на третьем уровне имеется ровно t3 состояний. И так да-

лее до получения tl состояний l го уровня все дуги с любыми надписями

ведут в состояние корзины.

Прочитав любое слово W, имеющее не более l букв, автомат A(L) переходит в одно определенное состояние S(W).

Пусть t = 2:

14

01

Sкорзина

F = fS0 = Se; SW : W 2 Lg

число состояний:

dim(A) = 20 + 21 + : : : + 2l + 1 = 2l+1 1 + 1 = 2l+1

Следствие:

Пусть есть jLj = k, l = max fjW1j; jW2j; : : : ; jWkjg, тогда dim(L) 6 2l+1.

5Минимальный автомат для регулярного языка

A = hX; S; ; S0; Fi автомат. dim(A) = jSj число состояний.

L = L(A), L 2 Reg

dim(L) = min dim(A)

A

15

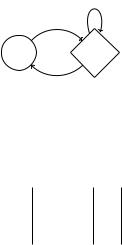
1

1

0

Доказательство: минимальности автомата (1) от противного. A(t; d), где t мощность алфавита, d множество состояний.

jA(t; d)j = X

Перемножим 1 2 3. Каждый член ячейки может принимать одно из значений d.

16

Вопрос 11

Вопрос 11. Объединение, пересечение или дополнение регулярных языков - регулярный язык.

Теорема1. Пусть L1; L2 2 Reg. Тогда L0 = L1 [ L2 2 Reg.

Доказательство. Т.к. L1 è L2 - регулярные языки, мы можем пострить распознающие их КДА (L1 ! L1 = L(A1); L2 ! L2 = L(A2)):

A1 =< X; S1; 1; S10; F1 >

A2 =< X; S2; 2; S20; F2 >

Т.е. автомат будет принимать те слова, которые входят хотябы в один из языков L1 èëè L2.

Автомат построен и он распознает нужный язык ) теорема доказана. Теорема2. Пусть L1; L2 2 Reg. Тогда L0 = L1 \ L2 2 Reg.

Доказательство. Доказательство аналогично доказательству предыдущей теоремы. Т.е. мы строим КДА A', распознающий L'. Отличие лишь

в определении принимающих состояний нового автомата:

F0 = fs0 : s0 = (s01; s02); s01 2 F1&s02 2 F2g

Теперь автомат принимает только те состояния, которые являются принимающими одновременно для обоих автоматов языков L1 è L2. Автомат построен ) теорема доказана.

Теорема3. Пусть L 2 Reg. Тогда L = X n L 2 Reg.

Доказательство. Основа доказательства такая же, как у предыдущих двух, т.е. надо построить новый автомат. Но на этот раз мы строим автомат для дополнения. Поэтому просто меняем местами "хорошие"и "плохие"состояния. Итак, если язык L распознается автоматом А:

17

A =< X; S; ; S0; F >,

то автомат, распознающий язык L будет отличаться лишь принимающи-

ìи состояниямè:

A =< X; S; ; S0; F >

F = S n F

Т.е. те состояния, которые были принимающими, становятся не принимающими и наоборот. Таким образом, автомат A принимает только те

слова, которые не принимает А, что и требовалось. Итак, автомат построен ) теорема доказана.

18

Вопрос 12

Вопрос 12. Следствия теорем. Объединение и пересечение конечного числа регулярных языков - регулярный язык.

Теоремà1. (Следствие Теоремы3 предыдущего пункта) dim(L) dim(L)

Доказательство. Пусть А - минимальный автомат, распознаюùèé ÿçûê

L: dim(L) = dim(A), тогда по определению автомата A : L = L(A) имеем:

dim(L) = dim(A) dim(A) = dim(L)

Что и требовалось доказать.

Теорема2. (Следствие Теорем 1 и 2 предыдущего пункта)

Åñëè L1; L2 2 Reg, L0 = L1 [L2 è L00 = L1 \L2, òî dim(L0) dim(L1)dim(L2) è dim(L”) dim(L1)dim(L2)

Доказательство. Доказательство следует сразу из определения построения автоматов A' и A00 äëÿ L', L00 , аналогично предыдущему доказатель-

ñòâó.

Теорема3. Пусть L1; L2; : : : ; Lk 2 Reg. Тогда булевая комбинация L языков L1; L2; : : : ; Lk 2 Reg - регулярный язык.

Доказательство. Доказательство следует из теорем 1-3 предыдущего пункта. Докажем для пересечения (объединение и дополнение аналогично) Воспользуемся методом математической индукции. Для объединения двух регулярных языков теорема уже была доказана. Пусть верно для k-1. До-

кажем для конечного k. Обозначив объединение k-1 языка через новый язык L0 2 Reg, можем вновь воспользоваться результатами теоремы1

предыдущего пункта. Т.к. L0 2 Reg è Lk 2 Reg, òî L0 \ Lk 2 Reg. Теорема доказана.

19

Вопрос 14

Булевы функции и языки

f : (0; 1)n ! (0; 1)

Lf = fw : f (w) = 1g; Lf Xn; X = f0; 1g

fLf

fLf = xnnLf

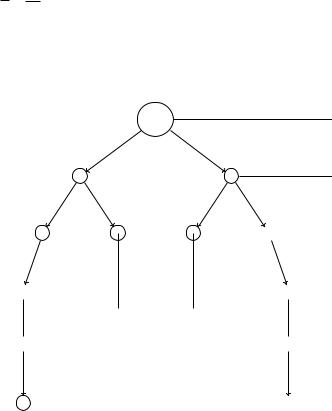
Теорема. Если f - произвольная булевая функция, тогда dim( fn) 2n+1 1

Доказательство. A =< X; S; ; s0; F >- полное бианрное дерево глубины n

22

2n

20 + 21 + 22 + + 2n = 2n+1 1

пример:

L

20