TEOR_inform_19-12-10_2014_01_06_12_12_03_442

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

sin m t n t

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

1.39 Mб

Скачать

☆

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

1.ТЕОРИЯ ИНФОРМАЦИИ

1.1Теорема Котельникова

Согласно теореме Котельникова, если спектр сигнала s ( t ) ограничен полосой Fm , то сигнал может быть восстановлен по своим отсчѐтам s ( n t ) , разделѐнными

интервалом времени t	1	:

	2 Fm
			Sin m	( t n t )
s ( t )		s ( n t )	Sin m	( t n t )
					,	(1.1)
					,	(1.1)
		n	m ( t n t )

где m 2 Fm .

Предполагается , что число отсчетов бесконечно, (интервал наблюдения - бесконечен ).

Ввиду того, спектр сигнала ограничен полосой Fm (вне этой полосы он равен ну-

лю), спектральную функцию сигнала можно представить как периодическую функцию. При увеличении интервала дискретизации tä больше, чем t , спектральные

функции сигнала на каждом периоде перекрываются, что приводит к искажению восстановленного сигнала. С уменьшением интервала дискретизации tä качество

восстановленного сигнала улучшается.

Если сигнал ограничен временем наблюдения TH , то можно осуществить периодическое продолжение его с периодом, равным TH . В этом случае производит-

ся дискретизация спектральной функции с интервалом f	1	, и производится

	2 TH

восстановление спектральной функции F ( ) по его отсчѐтам в частотной области:

		SinTH	( n )
F ( )	F ( n )
				,

	n	TH ( n )

где 2 f .

Восстановление спектральной функции будет улучшаться, если интервал дискретизации fä уменьшать по сравнению с f .

Рассмотрим приложение теоремы Котельникова к случайным процессам. Трудность непосредственной записи формулы (1.1) в применении к случайным процессам связано с тем, что имеется множество реализаций, случайного процесса. Поэтому применяется понятие сходимости в среднеквадратическом [*Левин кн 2 ]

Положим, (t) - непрерывный в среднеквадратическом, стационарный, хотя

бы в широком смысле, случайный процесс со спектральной плотностью мощности

F ( ) , m .

Если существует предел

тогда случайный процесс (t) определяется счѐтным множеством случайных

величин n

n m

		n			n

					2 fm
		2 fm

	n t и записывается
	n t и записывается

как

		sin m t n t
(t)	(n t)		.	(1.2)
		m t n t
	n

В качестве критерия возможности представления случайного процесса (t) в виде разложения (1.1) выберем равенство корреляционных функций процесса (t) правой части равенства (1.1). Положим, B ( ) - корреляционная функция процесса

(t) .

sin m t n t

Обозначим правую часть (1.1) через (t)

(n t)

. Кор-

m t n t

реляционная функция процесса (t) равна

sin m t n t

sin m

t k t

B n t,k t M (n t) (k t)

m t n t

m t k t

n k

sin m

t n t

sin m t k t

B n k

. *

m t n t

m t k t

n k

Сделаем замену

n k r,

n r k,

sin m t r t k

sin m t k t

B B

r t

m r

t k t

m t k t

Для произвольной задержки t0

справедливо разложение функции

sin m (t t0 )

m (t t0 )

ряд Котельникова и его представление в виде (Левин Б.Р. Статистические основы радиотехники, книга 2, стр.273 )

sin m (t t0 )		sin m (t k t)	sin m (t0 k t)

m (t t0 )		m (t k t)	m (t0 k t)
	k


Применяя это соотношение к M (tk ) (tn )		, получим

k n

sin

t t r t

M (tk ) (tn )

B r t

t t r t

sin m r t

sin m

r t

B r t

m r t

Но учитывая, что корреляционная функция – четная функция, имеем

sin m

r t

M (tk ) (tn )

B r t

(1.3)

r t

Но (1.6) - есть разложение корреляционной функции B по ортогональным

функциям вида

sin x

т.е.

B = M (tk ) (tn ) .

k n

Исходя из принятого критерия, получим равенство (1.1)

1.2 Квантование сигнала по уровню

Положим, дискретизация сигналов по времени произведено, и необходимо передавать сигналы в дискретные моменты времени. Можно передавать сигналы, используя амплитудно-импульсную модуляцию (АИМ). Однако в настоящее время широко внедряются в практику кодово-импульсная модуляция (КИМ). Суть в следующем. Значения импульсов, полученных в результате дискретизации, переводятся в последовательность стандартных импульсов. Каждому значению параметра сигнала после дискретизации по времени соответствует определѐнный набор импульсов. Но при переходе от непрерывного представления параметра к дискретному возникает проблема, как выбирать порог дискретизации.

Для этого все возможные непрерывные значения параметра сигнала разбиваются на неперекрывающиеся интервалы квантования длиной k , k 1, 2, , m ,

где m - число интервалов квантования. Длины интервалов квантования могут быть неравными. Внутри каждого интервала квантования произвольно выбирается точка xk - уровень квантования. Если значение параметра сигнала попадает в k -ый ин-

тервал k , оно заменяется величиной xk . В результате имеется дискретный набор

возможных значений параметра сигнала xk , k 1, 2, , m . Но в результате квантования возникает ошибка квантования, связанная с замещением истинного значения параметра его приближенным значением xk . Рассмотрим отдельно k -ый ин-

тервал k . Обозначим

границы

k -ого

интервала через

xk 1/ 2 ,

x (xk 1/ 2 , xk 1/ 2 ],

рисунок 11. Ве-

личина k -ого интервала квантования

будет равна

k xk 1/ 2 xk 1/ 2

xk -1/2

Ошибка квантования xk , истин-

ное значение x и уровень квантова-

xk+1/2

ния xk связаны соотношением

δk

x xk .

(1.4)

Как видно из (1.7) и рисунка 1.1

Рис. 1.1 Ошибка квантования xk

для

ошибка

квантования на интервале

заданного уровня квантования xk

квантования k зависит от положения

уровня квантования

xk . Поэтому воз-

никает вопрос, как расположить уровень квантования относительно границ xk 1/ 2 ,

xk 1/ 2 .

Положим, непрерывные значения сигнала распределены по неизвестному закону с плотностью распределения вероятности w (x) . Математическое ожидание ошибки

квантования xk , с точки зрения теории измерений, определяет систематическую

ошибку, а дисперсия ошибки квантования - динамическую ошибку, т.е. разброс случайных значений параметра сигнала около математического ожидания. Примем в качестве критерия выбора положения уровня квантования xk равенство нулю систематической ошибки

M[ xk ] xxk 1/ 2 (x xk ) w (x) dx 0 .	(1.5)
k 1/ 2

Ввиду того, что плотность распределения вероятности w (x) не известна и интер-

валы квантования k достаточно малы, примем значения плотности распределения

вероятности		w (x)		постоянной в интервале (x	k 1/ 2	, x	k 1/ 2	], равной	w (x* ) , где
					k 1/ 2		k 1/ 2			k
x* (x	k 1/ 2	, x	k 1/ 2	]. В результате из (**.2) получим
k	k 1/ 2		k 1/ 2
				xxk 1/ 2 (x xk ) dx 0 .					(1.6)
				k 1/ 2

Решением этого приближенного равенства будет

xk	1	xk 1/ 2 xk 1/ 2 .	(1.7)
	2

Из выражения (**.4) видно, что уровень квантования xk при сделанных допу-

щениях должен находиться в середине интервала квантования.

Дисперсия ошибки квантования (динамическая ошибка) с учетом сделанных выше предположений равна

D[ xk ] xxk 1/ 2 x xk M[ xk ] 2 w (x) dx
k 1/ 2
w (xk* ) xk 1/ 2 x xk 2 dx		1	w (xk* ) k3 .	(1.8)
w (xk* ) xk 1/ 2 x xk 2 dx	12		w (xk* ) k3 .	(1.8)
xk 1/ 2	12

Ввиду того, что интервалы квантования не перекрываются, ошибки квантования будут независимыми и общая дисперсия ошибки квантования равна сумме дисперсий ошибок квантования на каждом интервале, т.е.

D[ x] D[ xk ]		1	w (xk* ) k3 .	(1.9)
	12
k			k

Выбор длин интервалов квантования k зависит от априорных данных. Существуют различные методы выбора интервалов квантования. В самом простейшем

случае

интервалы

квантования

могут

быть

равны между собой, т.е.

k ,

k 1, 2, . Тогда выражение (**.6) будет иметь вид

D[ x]

w (xk* ) .

(1.10)

Произведение w (x* ) - приблизительно равно вероятности того, что изме-

ряемая величина принадлежит интервалу (x

, x

1 ]. Погрешность аппроксима-

ции зависит от величины интервала . По условию нормировки

w (xk* ) 1.

(1.11)

Используя (**.7) и (**.8) , получим

D[ x]

12 .

(1.12)

Среднеквадратическая ошибка квантования равна

R[ x]

2.Мера информации

2.1Мера информации по Шеннону

Сообщения могут быть закодированы разными символами. Число разных символов, из которых образуются сообщения, составляет основание кода, (русский алфавит имеет 33 символа, двоичный код – 2 символа, код Бодо – 5 символов и т.д.).

Совокупность различных символов, составляющих основание кода, назовем алфавитом.

Пусть m - основание кода и передается последовательность x1, x2 , , xk , где xi - один из символов из алфавита. Число всевозможных сообщений, которые

можно создать равно N m k . Информация, содержащаяся в ансамбле из N сообщений, должна быть пропорциональна длине последовательности. Р. Хартли в 1928 г. предложил за меру количества информации в ансамбле из N сообщений принять величину

I x log N k log m.

Но мера информации по Хартли не учитывает вероятностный характер появления элементов последовательности x1, x2 , , xk .

Мера – это одна из характеристик исследуемого объекта. Это может быть длина, ѐмкость и т.д. В данном случае необходимо определить меру информации, содержащемся в каждом элементе ансамбля и среднюю меру информации в ансамбле в целом.

Мера должна обладать двумя свойствами:

1.мера исследуемого объекта не должна быть отрицательной,

2.если объект состоит из нескольких элементов, каждый обладающий определѐнной мерой, полная мера объекта равна суме мер отдельных составляющих, (условие аддитивности) .

Пусть ансамбль X состоит из элементов x1, , xi , , x j , , xN . Выберем два элемента xi , x j из этого ансамбля, имеющих совместную вероятность реализа-

ции этих элементов

p(xi x j ) p(xi ) p(x j / xi ).

Обозначим через ( ) меру информации, содержащемся в элементе . Тогда, используя свойство аддитивности меры, запишем меру информации, содержащуюся в ансамбле из двух элементов xi , x j ,

( p(xi x j )) ( p(xi ) p(x j / xi )) ( p(xi )) ( p(x j / xi )) .

(2.1)

Дифференцируя левую и правую части выражения (**.1) по p(xi ) , получим

C 1/ ln 2

d ( p(xi x j ))	d ( p(xi x j )) dp(xi x j )		d ( p(xi	))	.
dp(xi )	p(xi x j )	dp(xi )	dp(xi )

dp(xi x j )

d ( p(xi ) p(x j / xi ))

p(x j

/ xi ) .

dp(xi )

В результате имеем

d ( p(xi x j ))

d ( p(xi ))

p(x j / xi

)

dp(xi

p(xi x j )

)

Умножив обе части полученного равенства на p(xi ) , получим уравнение

d ( p(xi x j ))

d ( p(xi ))

p(xi , x j )

p(xi ) .

(2.2)

dp(xi )

p(xi x j )

Уравнение (***.2) имеет решение, если

d ( p(xi x j ))

d ( p(xi

))

p(xi , x j )

p(xi )

C ,

(2.3)

dp(xi )

p(xi x j )

где С – постоянная величина.

Интегрируя уравнение (***.3), получим

d ( p(xi ))

dp(xi ) ,

p(x

)

( p(xi )) C ln ( p(xi )) C0

(2.4)

Определим C0

из условия: если

событие xi происходит

с вероятностью

p(xi ) 1, то оно не несѐт никакой информации для абонента. Поэтому функция

( p(xi ) 1) 0 и C0 0.

Так как мера информации не должна быть отрицательной, а p(xi ) 1, то ко-

эффициент C должен быть отрицательным. Если C 1, то мера информации имеет вид

( p(xi )) ln ( p(xi ))

иизмеряется в неперах, [Неп]. Однако на практике, ввиду развития цифровой тех-

ники и использования двоичной системы счисления чаще применяется основание логарифма, равное 2. Тогда и мера информации, или количество информации, содержащаяся в элементе xi , будет равна

(xi ) ( p(xi )) log 2 ( p(xi )) .

(2.5)

В дальнейшем основание логарифма 2 будем опускать. Мера информации (xi ) измеряется в битах, (Бит).

Каждый элемент ансамбля обладает своим количеством информации (xi ) , реализующимся с вероятностью p(xi ) . Таким образом, мера информации – это характеристика элемента ансамбля X , являющаяся случайной величиной с реализациями в виде количества информации (xi ) , появляющихся с вероятностями

		k	p(xi ) 1, (Таблица 1).
p(xi ),	i 1		p(xi ) 1, (Таблица 1).
	i 1
		Таблица 2.1

			X	x1	xk
			P	p(x1)	p(xk )
			(xi )	log ( p(x1))	log ( p(xk ))

2.2 Энтропия дискретного ансамбля сообщений

Среднее количество информации, содержащееся в ансамбле X , определяется математическим ожиданием

	M I ( X ) H X =		k
	M I ( X ) H X =		i 1	p(xi ) log ( p(xi )) .	(2.6)
			i 1
Величина H X называется энтропией ансамбля X и имеет размерность
áèò					X : это
		. Под термином сообщение понимается элемент ансамбля
		. Под термином сообщение понимается элемент ансамбля
ñî î áù åí èå

может быть символ или набор символов, образующих некоторое сообщение и т. д. Пример 1.Положим, x1, x2 , x3 , x4 образуют ансамбль сообщений X . Вероятности реализаций этих сообщений соответственно равны p(x1) 0.1, p(x2 ) 0.4,

p(x3 ) 0.2, p(x4 ) 0.3. Определим количество информации, содержащуюся в

каждом сообщении, и меру неопределѐнности в ансамбле X . После расчетов получим

(x1 ) 3.3219 áèò , (x2 ) 1.3219 áèò , (x3 ) 2.3219 áèò ,

(x4 ) 1.7369 áèò .

Энтропия ансамбля равна H X 1.84644	áèò	.


	ñî î á.

Как видно, наибольшее количество информации содержится в сообщении x1 , которая реализуется с наименьшей вероятностью, и наименьшее количество информации содержится в сообщении x2 , вероятность реализации которой наиболь-

шая. Чем ближе к единице вероятность реализации сообщения, тем меньше информации содержится в этом сообщении. Эти выводы хорошо согласуются с субъективным представлением о ценности получаемых сведений.

Пример 2. Положим, одно из сообщений ансамбля X реализуется с вероятностью p(xi ) 0. Тогда какое-то другое сообщение будет реализовываться с вероятностью p(x j ) 1. Вычислим энтропию вновь полученного ансамбля

X1 : xi , x j .

H X = p(xi ) log	1	p(x j ) log	1	0 log	1	.
	p(xi )		p(x j )		0

Получили неопределѐнность типа 0 . Разрешив эту неопределѐнность, получим H X = p(xi ) 0 . Неопределѐнность в ансамбле X 1 отсутствует.

Энтропия H X характеризует меру средней неопределѐнности ансамбля X

.Пусть задан ансамбль X : { x1, , xk } с распределением вероятностей

p(x1), , p(xk ) ,	k	p(xi ) 1. Тогда энтропия H X удовлетворяет нера-
p(x1), , p(xk ) ,	i 1	p(xi ) 1. Тогда энтропия H X удовлетворяет нера-
	i 1
венству
		0 H X log k .	(2.7)

Доказательство. Левая часть неравенства следует из определения энтропии ансамбля X . Для доказательства правой части рассмотрим разность H X log k и

t -1

преобразуем еѐ

H X log k

i 1 p(xi ) log p(xi ) i 1 p(xi ) log k =

i 1

p(xi ) log

ln t

k p(xi )

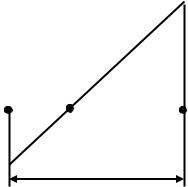
В дальнейшем используем неравенство t 1 lnt ,

Рис.2.1 Поведение

рисунок 2.1. Знак равенства будет только в случае

функций t -1 и lnt

t 1. Тогда имеем

H X log k

log e

p(xi )

-1 = log e

p(xi ) 0 .

i 1

i 1 k

i 1

k p(xi )

Из последнего неравенства следует, что знак равенства в правой части неравенстве (2.7) будет в том случае, если

1	= 1 или p(x	)	1	.

k p(xi )	i		k

Энтропия H X ансамбля X будет максимальной, если все события xi равно-

вероятны. Ценность информации в каждом xi	сообщении, с точки зрения частоты
еѐ появления в результате опытов, будет равна	(xi ) log 2 k .

Вычислим энтропию произведения ансамблей X : x1, , xk и Y :y1, , yk . Произведение ансамблей образует матрицу сообщений

	x y
X Y		1	1
X Y

	xk y1

с распределением вероятностей

	p x1 y1

P X Y
p x		k	y
		k	1

x1 yk

xk yk

	p x	y
	1	k
		.

p xk yk

Пользуясь определением энтропии ансамбля, запишем энтропию произведения ансамблей

M I (X Y ) H X Y =

i 1 j 1

p(xi

y j ) log ( p(xi y j )) =

i 1

j 1

p(xi y j ) log ( p(xi ))

i 1

j 1

p(xi y j ) log ( p( y j / xi )) =

p(xi ) log ( p(xi )

i 1

i 1 j 1

p(xi y j ) log ( p( y j / xi )) =

H X H Y / X H Y H X / Y

(2.8)

H Y / X

Условная энтропия

i 1

p(xi y j ) log ( p( y j / xi ))

зависит

j 1

от условной меры информации I ( y j / xi ) log ( p( y j / xi )) - количества ин-

формации, содержащаяся в сообщении y j , при условии, что уже реализовалось со-

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.02.2015625.89 Кб17Teoria_gosudarstva_i_prava.pdf
#
10.02.2015519.73 Кб45Teoria_igr_2012_2013.pdf
#
22.09.201935.65 Кб2Teoria_i_praktika_SMI-_lektsii.docx
#
10.02.201523.34 Mб15Teoria_sistem_i_sistemny_analiz_-_lektsii_1-11.pdf
#
10.02.20151.11 Mб26Teorinf.pdf
#
10.02.20151.39 Mб3TEOR_inform_19-12-10_2014_01_06_12_12_03_442.pdf
#
23.03.20161.17 Mб36termodinamika.doc
#
23.11.2019297.47 Кб1termostat!33.doc
#
12.03.20151.87 Mб18TERVER_13-14.pdf
#
13.04.2019558.08 Кб0Testy_2009_po_filosofii (2).doc
#
14.07.20191.18 Mб4Testy_GP_ch_2 (1).rtf