Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

TEOR_inform_19-12-10_2014_01_06_12_12_03_442

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

1.39 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

4.3 Канал с шумами

Наличие шума в канале связи приводит к тому, что условная энтропия

H Z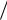Y не равна нулю. Условную энтропию H ZY Шеннон назвал ненадѐж-

ностью канала, так как она зависит от шума в канале связи. В результате возникает вопрос, существует ли метод кодирования, позволяющий передавать информацию

сопределѐнной скоростью Rè áèò . На это вопрос отвечает теорема Шеннона

ñåê

(Шеннон стр.280).

Пусть дискретный канал обладает пропускной способностью

C	áèò	, а дискретный источник – энтропией H X	áèò	. Если


	ñåê		ñî î á

Rè < C , то существует такая система кодирования, что сообщения

источника могут быть переданы по каналу с произвольно малой частотой ошибок, (или со сколь угодно малой энтропией H Y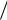Z ). Если Rè > C , то можно закодировать источник таким образом, что ненадѐжность H Y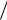Z канала будет меньше, чем Rè Ñ Vk ,

где сколь угодно мало. Не существует способа кодирования, обес-
печивающего ненадѐжность, меньшую, чем	Rè Ñ Vk .

Нет доказательства

Пример 4.1. Определим пропускную способность двоичного симметричного канала связи. Модель двоичного симметричного канала показан на рисунке 4.4.

В канал связи поступают симво-

q=1-p

лы 1 и 0, отображающие реальные

y1 1

физические сигналы.

1) Канал симметричный. Вероят-

ности искажения символов равны

y2 0

p 1 / 0

0 / 1 p , вероятности

неискажѐнного приема символов

Рис. 4.4

Модель двоичного

равны

симметричного канала связи	p 1 / 1 p 0 / 0 q 1	p .

2) Канал стационарный, так как условные вероятности не зависят от времени. Пропускную способность вычислим по формуле (4.8). Энтропию H Z определим

из условия H Z H Y при отсутствии шума. Энтропия H Y принимает мак-

симальное значение, равное 1, при p y1 p y2 0.5. Условная энтропия равна

H Z / Y p y1 p log p q log q p y2 p log p q log qp log p q log q

Подставляя полученные величины в (4.8), получим

C Vêàí 1 p log p q log q .

Как видно из формулы, пропускная способность зависит скорости поступления символов в канал и от вероятности искажения символов.

Положим, задан ансамбль сообщений X с распределением вероятностей P , (Таблица 4.2) . Сообщения генерируются со скоростью

Vè 100 ñî î á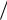ñåê .Способ кодирования определѐн и каждому сообщению припи-

Таблица 4.2

сан двоичный код. Энтропия ансамбля сообщений X равна

H X 1.659

áèò ñî î á ,

код

вероятности реализации символов «1» и «0» равны

0.6

p 1 0.249167,

p 0 0.750833,

энтропия ансамбля символов Y равна

0.2

0.8099551

áèò

ñèì â ,

0.1

110

1.7

ñèì â ñî î á .

средняя длина кода равна n

0.07

1110

Положим, в канале действует такой шум, что вероятность

ошибочного перехода равна

p 1 /

0 p 0 / 1 p 0.1.

0.03

1111

Сможет ли канал обеспечить передачу сообщений ?

Rè Vè H X 100* 1.659 165.9

áèò

ñåê

2) Будем считать R

. Тогда V

100* 1.659

= 204.826

ñèì â

êî ä

0.8099551

ñåê

Будем считать Rêàí

Rêî ä . Тогда Vêî ä

Vêàí и пропускная способность ка-

нала равна C Vêàí

1 p log p q log q

= 204.826 1 0.1 log 0.1 0.9 log 0.9 =

108.764 áèò

ñåê

Как видно, пропускная способность канала значительно ниже скорости генерации информации источником и часть информации может быть утеряна. В этом случае можно уменьшить скорость генерации сообщений Vè или уменьшить вероятность

ошибок p 1 / 0 p 0 / 1 p . Положим, каким-то образом удалось уменьшить вероятности ошибок до величины p 0.01. Тогда пропускная способность канала увеличится до величины C 188.277 áèò ñåê . При таком соотношении скорости поступления информации Rêî ä в канал и пропускной способности канала ис-

кажения информации в канале из-за величин Rêî ä и C не будет.

4.4 Непрерывный канал связи

Как и прежде, сигналы поступают в канал в дискретные моменты времени, но значения сигналов принимают непрерывные значения из некоторого множества. Примером такого канала является передача амплитудно-модулированных, фазомодулированных или частотно-модулированных сигналов. Сами сигналы могут быть как детерминированными, так и являться случайными процессами. Сигнал и шум взаимно независимы и в канале связи складываются алгебраически, т.е сигнал и

шум аддитивны
	Z ti Y ti ti ,	i 1,2, ,	(4.15)
где ti -	шум в канале с известной плотностью вероятности w ri ,

Y	ti - непрерывный по множеству значений сигнал, поступающий в канал
связи.	Плотность распределения вероятности wY yi значений сигнала может
быть произвольной
Чтобы упростить записи, в дальнейшем будем писать
			Zi Yi i ,	i 1,2, ,			(4.16)
помня,	что Zi , yi , i	-	непрерывные		величины, а их реализациями		являются
zi , yi , ri . Запишем равенство (4.16) через реализации
			zi yi ri ,	i 1,2,			(4.17)
Условная плотность распределения w zi yi при фиксированном значении
yi должна удовлетворять соотношению
	wZ	y zi yi dzi w ri dri .					(4.18)
Используя (**.17), получим условную плотность распределения
	wZ y zi		yi w ri		dri	w zi yi	(4.19)
	wZ y zi		yi w ri			w zi yi	(4.19)
					dzi

Пропускная способность непрерывного канала связи определяется подобным образом, что и для дискретного канала, но максимизация пропускной способности

производится по всем возможным распределениям wY y :
C max	J Y; Z	max	H Z H Z / Y

wY y	T	wY y		T
max Vk	H Z	H Z / Y		áèò	,	(4.20)


w y				ñåê
Y

где T - время, затраченное на передачу одного значения yi ,

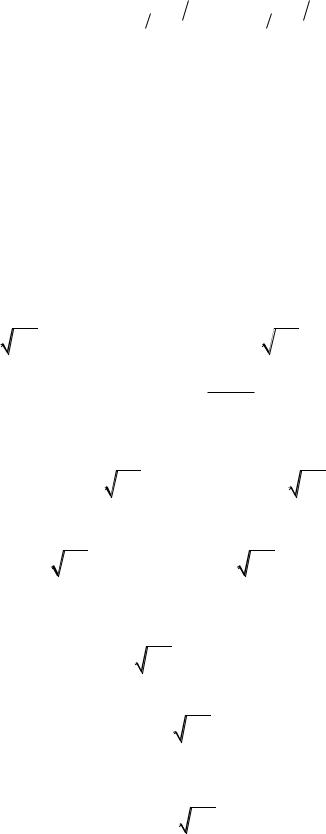
Vk - скорость передачи сигналов в канале - количество значений yi , передан-

ных по каналу в единицу времени.

Определим условную энтропию H Z / Y :

H Z / Y w y, z log w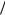Z y z y dy dz

wY	y wZ	y z	y log wZ y z y dz dy
Y	Z
wY y w z y log w z y dz dy				(4.21)

Y Z

Из (4.21) видно, что условная энтропия H Z / Y зависит от плотности распреде-

ления вероятности шума.

Пример 4.3. Вычислим энтропию случайной величины Y , подчиненной нормальному закону с математическим ожиданием, равным m, и дисперсией, равной

Y2 .

H Y	wY y log wY y d y =

	1		y m 2
		exp	2


2	Y		2 Y
2	Y		2 Y

Сделаем замену переменных x


log

y m

1		y m 2
	exp		d y
	exp		d y
2 Y		2
2 Y		2 Y

, dy x Y .

		H Y									1									x	2											1									x	2
											1		exp							x			log									1			exp						x			d x
													exp										log												exp									d x
											2								2													2									2
											2								2													2									2
																																		Y
							1							x	2												1												x		2
							1				exp			x				log									1						log exp						x				d x
											exp							log															log exp										d x
						2						2														2													2
						2						2														2													2
																														Y
		1										1												x	2
		1	log		2 2							1				exp								x			d x
			log		2 2											exp											d x
2							Y						2										2
2													2										2
																1												x		2						x		2
								log e								1						exp						x				ln exp				x				d x
								log e														exp										ln exp								d x
																	2										2										2
																	2										2										2
1				2 2					1								x		2										x		2
1	log								1	log e							x					exp							x				d x
	log									log e												exp											d x
2					Y			2										2									2
2								2										2									2

log 2 e 2 .

Как видно, энтропия H Y

не зависит от математического ожидания m.

Пусть H Y

- энтропия случайной величины Y

с математическим

ожиданием, равным нулю,

и дисперсией, равной

2 . Энтропия слу-

чайной величины Y

не превышает энтропии нормального закона

распределения вероятности

2 e Y2 ,

H Y

log

(4.22)

где знак равенства имеет место тогда и только тогда, когда случайная

величина Y распределена по нормальному закону.

Положим, wY y

- произвольная плотность распределения вероятности слу-

чайной величины Y . Случайная величина подвергается преобразованию

Y 2

2 2

log

Определим математическое ожидание случайной величины

2 2

M wY y log

dy =

2 Y

y dy

log 2 e Y2 .

log

log e

(4.23)

2 Y

2 e Y2

. Правая часть этой разности есть

Рассмотрим разность H Y

log

. Поэтому

H Y

log 2 e Y2

wY y log wY y dy wY y log

2 2

2 Y

2 2

y log

			1			e y	2
log e wY	y		1
			y
				2
	w			2
		Y			Y

	1		y2	2 2	dy wY
log e		e		Y
				Y

	2 Y
	2 Y

2 2
Y	1 dy

y dy 0.

Знак равенства будет только тогда, когда справедливо равенство

2 2

1 0 или

e y2 2 Y2 .

2 Y

Таким образом, энтропия достигает максимального значения при нормальном законе распределения вероятности. При этом накладываются условия:

-дисперсия Y2 случайной величины ограничена,

-область определения плотности распределения вероятности – ( , ).

При рассмотрении пропускной способности канала связи никаких ограничений на вид распределения вероятности шума не накладывалось. В частном случае, наиболее употребляемом на практике, предполагается, что шум - нормальный белый. Это означает, что значения шума распределены по нормальному закону и они не коррелированны. При таких предположениях имеет место теорема Шеннона (Фано,

стр. 176)

Если в непрерывном постоянном канале с дискретным временем аддитивный шум имеет гауссовское распределение с нулевым средним и дисперсией, равной Pø , а мощность сигнала на входе не может пре-

вышать определенной величины Pñ , то пропускная способность этого

канала на событие определяется формулой

	1			P
C	1	V	log 1	c	.	(4.24)
C		V	log 1		.	(4.24)
	2 êàí			P
				ø

Знак равенства достигается лишь тогда, когда сигнал на входе канала - гауссовский с нулевым средним и дисперсией, равной Pñ .

Как известно, пропускная способность канала имеет вид

wY y k

max V

Z / Y

Определим H Z / Y

. Из соотношений (4.15) -

(4.18) следует,

Z y

w r

. В силу независимости сигнала и шума P

По определению

P .

H Z / Y wY y wZ

y z

y log wZ y z

y dz dy .

y zi

yi плотность распределения

Подставим

вместо

условной плотности

шума и, учитывая, что шум распределѐн по нормальному закону, получим

H Z / Y wY

y w ri log w

ri dr dy

log

2 e Pø .

(4.25)

Используя общее определение пропускной способности канала (4..20)

C max V

H Z

Z / Y max V

log 2 e P

w y k

Pø

max

log

max

log 1

(4.25)

w y

2 k

y 2 k

Если сигнал на входе канала распределен по нормальному закону, то и сумма (4.16) также распределена по нормальному закону, что является необходимым условием максимального значения энтропии H Z . В этом

случае пропускная способность достигает максимального значения (знак равенства в (4.24)).

4.5 Теорема Шеннона о пропускной способности

частотно ограниченного канала

Передача информации тесно связана с использованием физических сигналов. Свойства сигналов определяют канал связи. Известно, сигнал может быть представлен во времени и через спектральное разложение. Рассмотрим влияние ограничения на сигнал во временной и частотной областях и влиянии этих ограничений на пропускную способность канала связи.

1) Положим, сигнал s ( t ) определѐн в интервале t и задана полоса частот Fm , занимаемая сигналом s ( t ) . Тогда, согласно теореме Котельникова,

сигнал	s ( t ) может быть разложен по функциям типа								Sin x	со значениями коэффи-
сигнал	s ( t ) может быть разложен по функциям типа								x	со значениями коэффи-
									x
циентов разложения, равными значениям сигнала в точках отсчета,
							Sin m ( t n t )
	s ( t )			s ( n t )			Sin m ( t n t )	,		(4.26)
	s ( t )			s ( n t )			m ( t n t )	,		(4.26)
			n				m ( t n t )
где m	2 Fm ,	t		1		.

					2 Fm
					2 Fm

Ограничим время наблюдения интервалом (0, TH ). Тогда число отсчетов на интервале наблюдения равно

2 F T

(4.27)

m H

и в разложении сигнала s ( t )

число отсчѐтов ограничено:

FmTH

Sin m ( t n t )

s ( t )

s ( n t )

(4.28)

n FmTH

m ( t n

t )

Если стоит вопрос о точном восстановлении сигнала по его отсчетам, то это

невозможно, так как часть отсчѐтов будет утеряна.

Получили ряд (**.3), ограниченный по частоте и во времени

Мощность n-ой составляющей равна P

s ( n t )

2 .

s n

2) Положим задано время наблюдения TH сигнала s ( t ) . Из теории рядов Фурье известно, что можно построить периодическое продолжение функции s ( t ) с пе-

риодом TH . Разложим сигнал s ( t )							в ряд Фурье

				s ( t )	Ck e j k t			Ck e j k 0 t ,		(4.29)
					k			k
где			2	.
где	0			.
	0	TH
		TH
Коэффициенты разложения вычисляются по формуле
								T / 2
					Ck	1		H	s ( t ) e j k 0 t dt
					Ck			H	s ( t ) e j k 0 t dt
					TH T				/ 2
								H

Чтобы ряд (**.4) сходился, необходимо выполнения условия - последовательность


Ck	должна быть убывающей и	Ck	2 .
Ck	должна быть убывающей и	Ck	2 .
	k

Выберем достаточно большое число m, чтобы можно было пренебречь величиной

( m 1)

2 . Тогда Fm m F1

, или m Fm TH .

k m 1

Разложение сигнала s ( t ) ограничено числом отсчетов

Fm TH

j k 0 t

s ( t )

(4.30)

k Fm TH

Получили ряд, ограниченный по частоте и по времени.

					2
Мощность k-ой составляющей равна P			C	k	2	. Мощность сигнала равна мощно-
		s k		k
	2 Fm TH
сти составляющих Ps		Psk

3)Так как шум, присутствующий в канале, также ограничен по частоте и во

времени определим числовые характеристики шума. Считается, что число отсчѐтов уже известно, т. е. определены Fm и TH .

Примем M ( t )

0 ,

шум – «белый», т.е. M ( t

) ( t

)

( t

) .

Разложение шума ( t ) по гармоническим составляющим

( t )

e j k 0 t

(4.31)

k F

k 0

коэффициенты разложения равны

TH 2 ( t ) e j k 0 t dt .

TH T

Согласно определению случайного процесса математическое ожидание и дис-

персия коэффициентов разложения будут равны

M ( t ) e j k 0 t

dt 0 ,

TH T

j k 0

( t 2 t1 )

( t

) ( t

)

dt dt

TH 2

( t2 t1 ) e j k 0 ( t 2 t1 ) dt1 dt2

TH2

j k t

( t2

t1 ) e

2 dt2

dt1

2TH2

T 2

N0	TH	2 e j k 0 t1	e j k 0 t1	dt1	N0	.
2T 2
					2TH
H TH		2

Мощность шума в канале связи равна

	2 Fm TH				N0
P D ( t )		D		2 F T	N0	F N		.
P D ( t )		D		2 F T		F N		.
ø			i	m H 2T		m	0
	i 1				H

4) Теорема Шеннона для частотно ограниченного канала.

Если мощность сигнала на входе канала не превосходит величины

(4.31)

(4.32)

Ps ,

то пропускная способность частотно ограниченного канала с аддитивным белым гауссовым шумом удовлетворяет неравенству

C ≤ F

log

1 +

(4.33)

Fm N0

Знак равенства будет в том случае, когда значения сигнала распреде-

лены по нормальному закону.

Согласно определению пропускной способности

2 Fm T

; Z

2 Fm T

lim

max

TH w ( y )

2 Fm T

lim max

(4.34)

TH w ( y )

2 Fm T

- это энтропия множества отсчетов в моменты вре-

Энтропия Z

мени ti с интервалом t из ансамбля Z для всех моментов времени ti . Ввиду того,

что неизвестны вероятностные характеристик процесса Y t , справедливы выражения

	2 Fm T		Z2	Z2 F T
Z	H	Z1	Z2	Z2 F T
				m H

Z	Z				2 Fm TH	Z	.

			Z	2 Fm TH				(4.35)
1		2		2 Fm TH	i 1	i
					i 1
			50

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.02.2015625.89 Кб17Teoria_gosudarstva_i_prava.pdf
#
10.02.2015519.73 Кб45Teoria_igr_2012_2013.pdf
#
22.09.201935.65 Кб2Teoria_i_praktika_SMI-_lektsii.docx
#
10.02.201523.34 Mб15Teoria_sistem_i_sistemny_analiz_-_lektsii_1-11.pdf
#
10.02.20151.11 Mб26Teorinf.pdf
#
10.02.20151.39 Mб3TEOR_inform_19-12-10_2014_01_06_12_12_03_442.pdf
#
23.03.20161.17 Mб36termodinamika.doc
#
23.11.2019297.47 Кб1termostat!33.doc
#
12.03.20151.87 Mб18TERVER_13-14.pdf
#
13.04.2019558.08 Кб0Testy_2009_po_filosofii (2).doc
#
14.07.20191.18 Mб4Testy_GP_ch_2 (1).rtf