
glava01
.pdf
К примеру, для электрического колебательного контура 2δ = RL ,
ω2 |
= |
1 |
, |
F(t) = E(t) , x = q. |
|
||||
0 |
|
LC |
|
L |
|
|
|
Наибольший интерес представляет случай гармонического воздействия, когда сила
F(t) = F0 cos( pt +ψ0 ).
Решение уравнения (1.31) – это сумма общего решения однородного уравнения (1.27) и частного решения неоднородного
x(t) = De−δt cos(ω t + ϕ) + X |
0 |
cos( pt + ψ |
0 |
+ ψ) |
(1.32) |
1 |
|
|
|
либо
x(t) = e−δt ( Acosω1t + Bsin ω1t) + X0 cos( pt + ψ0 + ψ) .
Частное решение неоднородного уравнения можно найти, к примеру, методомкомплексных амплитуд, представив F(t) = Re F0e j( pt +ψ0 ) , арешение
|
|
|
|
0e |
j( pt +ψ0 |
+ψ) |
. |
|
|
|
|
|||
|
|
|
x(t) = Re X |
|
|
|
|
|
|
|
|
|||
В результате можно получить |
|
|
|
|
|
|
|
|
|
|
||||
X0 |
= |
|
F0 |
|
|
, |
tg ψ = |
2δp |
. |
(1.33) |
||||
(ω2 |
− p2 )2 + 4δ2 p2 |
p2 |
− ω02 |
|||||||||||
|
|
|
|
|
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
Итак, решение (1.32) с учетом (1.33) показывает, что движение в системе в результате внешнего гармонического воздействия является суперпозицией двух движений: собственных затухающих колебаний и вынужденных колебаний с частотой внешней силы.
Амплитуда и фаза собственных колебаний зависят как от начальных условий, так и от параметров внешней силы (через константы A и B). Вынужденные колебания целиком определяются внешним воздействием. Со временем колебания по-разному ведут себя. Собственные колебания затухают и через время порядка нескольких τ =1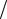 δ результирующий
δ результирующий
процесс будет определяться только вынужденными колебаниями, т. е. в системе остаются только вынужденные колебания, амплитуда и фаза которых задаются формулами (1.33). Формулы можно представить иначе,
введя безразмерные параметры: γ = |
p |
– относительную расстройку |
|
ω |
|||
|
|
||
|
0 |
|
частоты и Q = ω2δ0 – добротность колебательной системы.
29
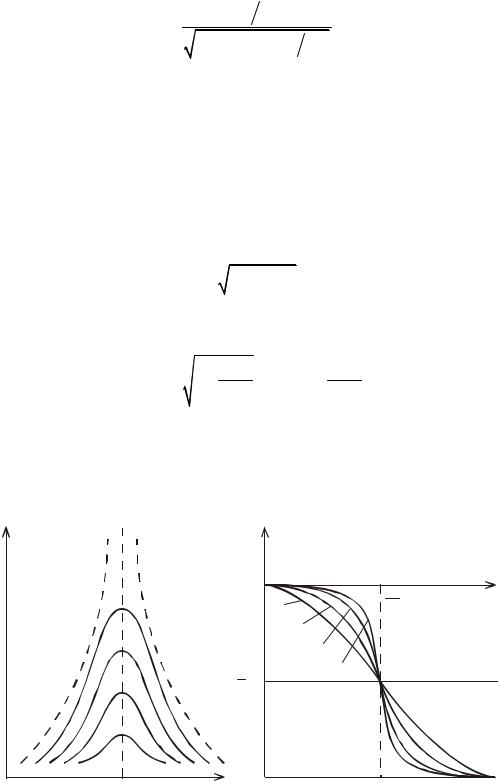
В этих обозначениях |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
F |
|
ω2 |
|
|
|
|
|
||
|
|
X0 = |
|
|
0 |
|
|
0 |
|
|
. |
|
(1.34) |
|
|
(1 − γ2 )2 + γ2 Q2 |
|
|
|
|
|||||||
Зависимость X0 от γ показана на рис. 1.12, а, где δ1 > δ2 > δ3 > δ4 > δ5 = 0. |
|||||||||||||
Видно, что максимальное значение |
амплитуды будет при |
p ≈ ω0. |
|||||||||||
Возрастание амплитуды вынужденных колебаний, когда частота внеш- |
|||||||||||||
ней силы близка к собственной частоте колебательной системы, называ- |
|||||||||||||
ется резонансом, а зависимость амплитуды вынужденных колебаний от |
|||||||||||||
частоты внешнего воздействия – резонансной кривой. Из рис. 1.14, а |
|||||||||||||
видно, что чем выше добротность (меньше потери), тем острее резонанс- |
|||||||||||||
ная кривая. Точное значение резонансной частоты можно найти, анали- |
|||||||||||||
зируя (1.34) на экстремум. Можно показать, что резонансная частота |
|||||||||||||
|
|
ωp = ω02 −2δ2 . |
|
|
|
|
|
||||||
Следовательно, чем больше добротность, тем ближе ωр к ω0. При |
|||||||||||||
Q >> 1ωp можно представить как |
|
|
|
|
|
|
|
|
|
|
|
||
|
ωp = ω0 1− |
|
1 |
|
|
|
− |
|
1 |
|
|
||
|
2Q2 |
ω0 1 |
4Q2 |
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
Рассмотрим теперь случай резонанса в системе без затухания. Пусть, |
|||||||||||||
к примеру, гармонический осциллятор в момент времени t = 0 покоится и |
|||||||||||||
на него начинает действовать сила F = F0 cos( pt + ψ0 ) . Из (1.32) следует |
|||||||||||||
X0 |
а |
δ5 = 0 |
|
|
ψ |
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
δ |
|
|
|
|
|
|
|
|
δ5 = 0 |
p |
||
|
4 |
|
|
|
|
|
δ1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
δ3 |
|
|
|
|
|
δ2 |
δ3 |
|
|
|
||
|
|
|
|
π |
|
|
δ4 |
ω0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
δ2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
δ1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
γ |
|
−π |
|
|
|
|
|
|
|
|
|
Рис. 1.14. Амплитудные (а) и фазовые (б) |
|
|||||||||||
|
кривые осциллятора для различных величин затухания |
|
|||||||||||
30
|
|
|
|
|
|
|
|
|
F0 |
|
|
|
|
x(t) = Acosω0t + Bsin ω0t + |
|
|
|
cos( pt |
+ ψ0 ) . |
|
|||||||
|
ω2 |
− p2 |
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Предположив, что в начальный момент времени x(0) = 0 , |
x(0) = 0, |
||||||||||||
придем к выражению |
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) = |
|
F0 |
|
(cos( pt +ψ |
|
|
) −cos(ω t +ψ |
|
))− |
|
|||
ω2 |
− p2 |
|
|
|
|
||||||||
|
|
|
0 |
|
0 |
0 |
|
|
|||||
|
0 |
|
|
|
|
|
|
|
|
|
|
. |
(1.35) |
|
|
|
|
F0 |
|
|
|
|
|
|
|
||
|
|
− |
|
sin ψ0 sin ω0t. |
|
|
|
||||||
|
|
ω0 (ω0 + p) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем значение амплитуды колебаний на частоте p = ω0, перейдя в (1.35) к пределу при p →ω0 :
x(t) = − |
F0 |
sin ψ |
0 |
sin ω t + |
F0t |
sin (ω t +ψ |
). |
(1.36) |
|
|
|
||||||||
|
2ω02 |
0 |
0 |
0 |
|
|
|||
|
|
|
2ω0 |
|
|
|
|||
В общем случае решение – сумма двух слагаемых, первое из которых обращается в нуль при равенстве нулю начальной фазы ψ0 вынуждающей силы. Второе слагаемое соответствует колебанию с линейно растущей со временем амплитудой. Следовательно, утверждение, что амплитуда колебаний консервативной системы при резонансе на частоте p = ω0 бесконечна, вообще говоря, неверно. В реальных системах возрастание амплитуды в конце концов ограничивается либо малым затуханием, либо нелинейностью.
Рассмотрим теперь фазовые соотношения между вынуждающей силой и откликом системы. Анализ выражения для фазы в (1.33) показыва-
ет, что при любой частоте |
p −π< ϕ< 0 , |
т. е. отклик всегда отстает по |
||||
фазе от воздействия. |
|
|
p |
|
|
|
Если |
ω0 >> p, |
то |
tg ψ ≈ ψ − |
; |
|
|
Qω |
|
|||||
|
|
|
|
|
|
|
|
|
|
tg ψ ≈ ω0 |
0 |
|
ω0 . |
если |
ω0 << p, |
то |
и ψ = −π + |
|||
|
|
|
Qp |
|
|
Qp |
Зависимость ψ от p приведена на рис. 1.12, б. Видно, что вне резонанса колебания гармонического осциллятора проходят либо в фазе, либо в противофазе с внешним воздействием (при достаточно высокой добротности). Строго в резонансе сдвиг фазы ψ = −π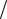 2 .
2 .
Применим полученные результаты в качестве примера для анализа последовательного электрического колебательного контура (см. рис. 1.13, б).
31

Выражение (1.33) в этом случае будет описывать амплитуду вынужденных колебаний заряда. Очевидно, что
dx |
= −pX0 sin( pt +ψ +ψ0 ), |
d 2 x |
= −p2 X0 cos( pt + ψ + ψ0 ) . |
|
dt |
dt2 |
|||
|
|
И тогда выражения для амплитудных значений напряжений на всех
элементах контура будут: на емкости |
|
UC |
|
= |
|
|
1 |
|
X0 |
|
, на индуктивности |
||||||||||||||
|
|
|
|
||||||||||||||||||||||
C |
|||||||||||||||||||||||||
|
UL |
|
= L |
|
p2 X0 |
|
|
|
UR |
|
= R |
|
pX0 |
|
|
|
|
|
|
||||||
|
|
|
|
, на сопротивлении |
|
|
|
|
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Путем нахождения экстремумов можно определить максимальные значения напряжений на элементах контура R, L, C:
|
|
U |
C |
|
|
|
=QE при p2 =ω2 |
− 2δ2 ; |
|||
|
|
|
|
|
|||||||
|
|
|
|
|
max |
0 |
|
||||
|
|
|
|
|
|
||||||
|
UR |
|
|
max = E при p2 =ω2 ; |
|||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
U |
L |
|
|
|
|
|
|
=QE при p2 =ω2 |
+ 2δ2 . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
max |
0 |
|
|||||
|
|
|
|
|
|||||||
Все три максимума совпадают только при Q →∞ ( δ →0). При не-
больших величинах добротности (Q = 2–5) резонансные максимумы отличаются друг от друга по частоте на несколько процентов.
В приведенных рассуждениях параметры колебательного контура считались постоянными, менялась только частота внешнего воздействия
p. В этом случае добротность контура Q = ω2δ0 = ωR0L = const. На практике
часто интересуются резонансными зависимостями, при которых частота внешнего воздействия p = const, а ω0 меняется за счет изменения одного из параметров – L или C. В этом случае добротность контура зависит от частоты, на которую настраивается контур. Резонансные зависимости отличаются от рассмотренных ранее.
Обобщим приведенные выше результаты анализа гармонического осциллятора на случай действия внешней периодической, но не гармонической силы.
Пусть F(t) = F(t +T ) , тогда такую функцию можно разложить в ряд Фурье по гармоническим компонентам с амплитудами An и частотами
pn = 2Tπn , n = 1, 2, 3 …, ∞.
Благодаря принципу суперпозиции отклик линейной системы на периодическую силу можно рассчитать как сумму откликов на действие
32
каждой гармонической компоненты. И решение можно сразу записать в виде
∞ |
An |
|
|
|
x(t) = ∑ |
|
|
cos( pnt +ψn ). |
|
|
− p2 )2 |
|
||
n=1 (ω2 |
+ 4δ2 p2 |
|||
0 |
n |
n |
||
Характер решения зависит от того, попадет ли частота хотя бы одной гармоники в область резонанса системы. Если такое n существует, то гармоника с этим номером оказывает определяющее воздействие на систему. Амплитуда такой гармоники значительно превышает амплитуды остальных гармоник и будет иметь место приближенное равенство:
x(t) |
|
An |
|
cos( pnt +ψn ). |
(ω2 |
− p2 )2 |
|
||
|
+ 4δ2 p2 |
|||
0 |
n |
n |
||
Таким образом, резонанс под действием непериодической внешней силы будет возникать, если собственная частота системы близка к часто-
те одной из фурье-гармоник внешней силы pn = 2Tπn и амплитуда этой гармоники не равна нулю.
1.7.ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Как отмечалось ранее, существует такой важный вид воздействия на колебательные системы, который заключается в том, что внешней силой производится изменение одного из параметров системы. Такой вид воздействия называется параметрическим.
Примерами осциллятора с изменяющимися параметрами могут служить электрический колебательный контур, емкость или индуктивность которого меняется во времени; маятник, точка подвеса которого совершает движение с ускорением в вертикальном направлении по заданному закону; качели, раскачивать которые, находясь на качелях, можно приседая и выпрямляя ноги в определенные моменты времени согласованно с движением самих качелей.
В рассмотренных примерах за счет изменения какого-либо параметра меняется частота колебательной системы. С физической точки зрения наибольший интерес представляют такие системы, которые в некотором смысле близки по своим свойствам к гармоническому осциллятору.
Почему это так, можно понять на примере электрического колебательного контура. Допустим, что в качестве емкости используется плоский кон-
33
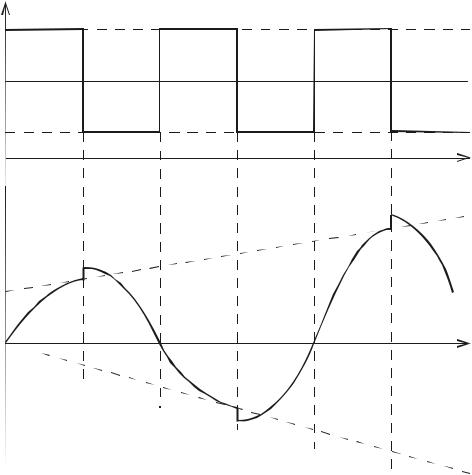
денсатор, в котором можно менять расстояние между пластинами. Предположим также, что заряд на конденсаторе меняется по закону, близкому к гармоническому. В момент, когда заряд на пластинах максимален, пластины резко раздвигают, изменив емкость на величину C. На преодоление сил притяжения будет затрачена энергия, которая преобразуется в энергию электрического поля конденсатора. При этом напряжение на конденсаторе скачком увеличивается. Через четверть периода заряд на пластинах оказывается равным нулю. В этот момент пластины резко сдвигают, так что емкость становится равной значению C0 + C. Когда заряд конденсатора снова оказывается максимальным, но противоположным по знаку заряду в начальный момент, пластины снова раздвигают, еще раз увеличивая напряжение, и т. д. Графики изменения C(t), U(t) показаны на рис. 1.15.
Очевидно, что в таком процессе постоянно будет совершаться работа, приводящая к увеличению энергии колебательного контура, а значит, и к росту амплитуды колебаний. Такое возрастание амплитуды колебаний при периодическом изменении параметров колебательной системы назы-
C0 + C
C0
C0 − C
t
U 
0 
t
Рис. 1.15. Изменение емкости в колебательном контуре и напряжения на ней при возникновении параметрических колебаний
34
вается параметрическим резонансом.
Для количественной оценки рассчитаем приращение энергии конденсатора W, которое получается в момент скачка емкости:
|
|
2 |
|
1 |
|
|
1 |
|
|
2 |
2 C |
|
|
|
|
W ′= q0 |
|
|
− |
|
|
|
q0 |
=W0 2m, |
|||
|
|
|
− C |
C0 |
+ |
|
C02 |
||||||
|
|
2 |
C0 |
|
C |
2 |
|
||||||
где |
W0 – |
энергия, |
запасенная в |
конденсаторе |
до скачка емкости; |
||||||||
m = |
C C0 |
– глубина модуляции параметра (емкости). |
|||||||||||
Общее |
приращение |
энергии |
в |
системе |
за |
период колебаний |
|||||||
W− = 2 W ′, поскольку за период пластины раздвигаются дважды.
Для определения условий параметрического возбуждения колебаний нужно сопоставить энергию, вводимую в контур за счет изменения емкости, с расходуемой на его активном сопротивлении. Энергия потерь в контуре за период
WR = 12 RI 2T. Если q = q0 sin ωt, то i = dqdt = ωq0 cosωt, а
|
|
|
|
|
|
W = 1 Rω2q2T = πRωq2. |
|
|||||
|
|
|
|
|
|
R |
2 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Полное изменение энергии за период |
|
|
|
||||||||
|
|
|
|
|
|
W = W − |
W |
= πωq2 |
R − |
2m |
. |
|
|
|
|
|
|
πωC |
|||||||
|
|
|
|
|
|
R |
− |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Можно ввести |
|
эквивалентное |
отрицательное сопротивление R− = |
||||||||
= |
2m |
. Если |
|
R |
|
> R , то вкладываемая энергия превосходит потери и |
||||||
|
|
|||||||||||
|
||||||||||||
|
πωC0 |
|
− |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
происходит нарастание амплитуды колебаний.
Процесс частичной или полной компенсации потерь в системе за счет ее внутренних свойств называется регенерацией. Для физического и математического описания систем, в которых имеет место регенерация, понятие отрицательного сопротивления используется достаточно широко. Формально C(t) можно заменить на C0 с вводом R− , и общее активное со-
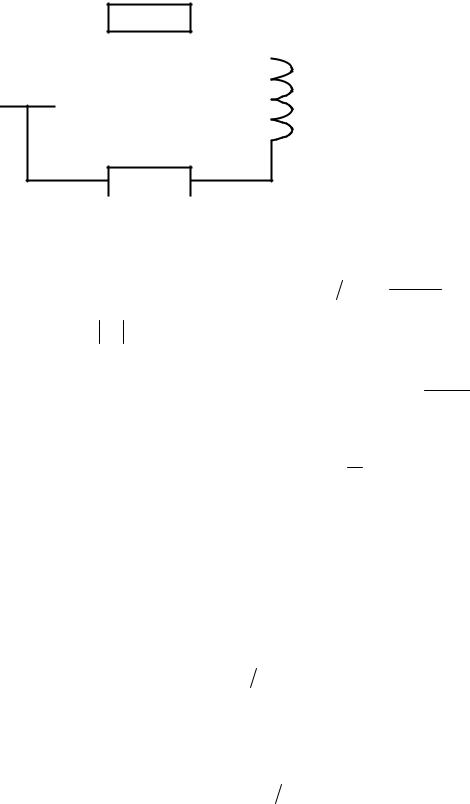
противление будет R′= R − R−(рис. 1.16). Если в подобный контур вводится внешний источник гармонического сигнала E = E0 cos pt, то при резонансе амплитуда тока будет равна I0 = E0  R − R−. Видно, что введение регенерации приводит к возрастанию резонансной амплитуды в кон-
R − R−. Видно, что введение регенерации приводит к возрастанию резонансной амплитуды в кон-
35
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
C0 |
|
L |
|
|
|
||
|
|
|
R− |
|
туре. Это явление лежит в основе работы различных регенеративных усилителей. Мощность, выделяемая на сопротивлении R, увеличивается, поскольку в регенеративном контуре
|
|
1 |
2 |
|
1 |
RU02 |
|
|
P1 |
= |
|
RI0 |
= |
|
|
, если ре- |
|
2 |
2 |
(R − R−)2 |
||||||
|
|
|
|
|
|
|
|
генерации |
нет, |
|
P |
= 1 RU02 |
. Та- |
||
Рис.1.16. Колебательный контур |
|
|||||||||
|
|
|
|
|
0 |
2 R2 |
|
|||
с эквивалентным отрицательным |
|
|
|
|
|
|
|
|||
ким |
|
|
|
|
|
образом, |
||||
сопротивлением |
|
|
|
2 |
||||||
|
|
|
P1 P0 |
|
|
R |
|
|
||
|
|
|
= |
R − R |
|
>1. |
|
|||
|
|
|
|
|
|
− |
|
|
|
|
Если же R− > R , то в контуре имеет место возбуждение колебаний за счет периодического изменения энергоемкого параметра (параметриче-
ское возбуждение колебаний). Учитывая, что R− = πω2mC0 , условие воз-
буждения колебаний можно записать в виде
m > mn = 12 πRC0ω= 12 Qπ = 12 d,
где mn – пороговое значение параметра модуляции.
Таким образом, при конечных потерях параметрическое возбуждение колебаний возможно только при определенной глубине модуляции параметра.
В рассмотренном примере параметр изменялся дважды за период возбуждаемых колебаний. Однако можно производить вложение энергии за счет изменения параметра 1 раз за период, 2 раза за три периода и в общем случае при выполнении условия
p = 2ω n, n = 1, 2, 3, …, |
(1.37) |
где p – частота изменения параметра; ω – частота вынуждаемых колебаний.
В практических схемах параметр изменяется не скачкообразно, а непрерывно, например, по закону, близкому к синусоидальному:
C(t) =C0 (1+ mcos pt). |
(1.38) |
Качественно результаты будут те же, изменится лишь выражение для порога модуляции.
36
Очевидно, что параметрическое возбуждение колебаний возможно лишь при изменении одного из энергоемких параметров C или L. Изменение R может привести лишь к изменению закона диссипации.
Отметим также, что в линейной колебательной системе при выполнении условия параметрического резонанса происходит неограниченное нарастание амплитуды возбужденных колебаний.
Проведенное выше рассмотрение параметрического возбуждения колебаний позволяет отметить его следующие существенные особенности.
Параметрический резонанс имеет место при определенном соотношении между частотой изменения параметра p и частотой возбуждаемых колебаний (см. (1.37)), при этом самым выгодным режимом является случай, когда p 2ω.
Параметрический резонанс возможен лишь при выполнении условий, определяющих изменение параметра модуляции m, m > mn для данного соотношения частот.
Важное значение имеют и фазовые соотношения между изменением емкости (накачкой) и напряжением на ней. Если изменить фазу накачки на противоположную, т. е. увеличивать емкость в моменты максимального заряда, то вложения энергии не будет, наоборот, имеет место отбор энергии. Это приведет к увеличению затухания в контуре.
Для развития параметрического резонанса необходимо, чтобы колебания в системе уже существовали. Если осциллятор покоится в положении равновесия, то изменение параметров не вызывает возникновения колебаний.
Математическое описание параметрического резонанса в линейных системах в общем случае производится с помощью линейного ДУ с переменными коэффициентами
x +ϕ1(t)x +ϕ2 (t)x = 0,
где φ1(t) и φ2(t) – периодические функции времени.
Частным случаем, соответствующим этому уравнению, является задача о параметрических колебаниях в контуре, емкость которого меняется по закону (1.38).
Уравнение колебаний примет вид
q + 2δq +ω02 (1 + mcos pt)q = 0.
Подстановкой q = e−δt x его можно свести к уравнению Матье:
x +(ω02 −δ2 + mω02 cos pt)x = 0.
37
Общее решение данного уравнения:
x =C1eλ1t Φ1(t) + C2eλ2 t Φ2 (t) ,
где C1, C2 – произвольные постоянные; Φ1, Φ2 – периодические функции времени.
Процесс, описываемый этим решением, определяется величинами λ1 и λ2. Если λ1 и λ2 – комплексные и Reλ1 < 0, Reλ2 < 0, то будут иметь место затухающие колебания, при Reλ1 > 0, Reλ2 > 0 – колебания нарастающие. Полный анализ решений математически довольно сложен и сводится обычно к нахождению таких областей значений соотношения частот 2ω0 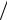 p и глубин модуляции m, для которых возможен параметрический
p и глубин модуляции m, для которых возможен параметрический
резонанс [5, 6].
Результаты этих расчетов в виде графиков показаны на рис. 1.17. Возбуждение параметрических колебаний возможно внутри областей,
ограниченных пунктирными (для систем без затухания) или сплошными (для систем с затуханием) линиями (рис. 1.17, а). Частота колебаний
ω= 2p n ω0 , n = 1, 2, 3, … . Видно, что существует бесконечно много
областей параметрического возбуждения колебаний. Ширина области с одним и тем же номером всегда меньше у диссипативной колебательной системы по сравнению с консервативной. Поскольку с ростом номера n поступления энергии в систему происходят реже, ширина области параметрического возбуждения становится меньше при одном и том же значении параметра модуляции m. Наличие затухания приводит к появлению порога затухания, величина которого для каждой области определяется прямой tg ϕ = 2δ. Очевидно, что для выбранного значения глубины
m |
а |
б |
|
A |
|
|
|
 tg ϕ = 2δ
tg ϕ = 2δ
|
ϕ |
|
3 2ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
1 |
2 |
0 |
|
1 |
|
2 |
|
3 2ω0 |
||||||||||||
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
Рис. 1.17. Области возбуждения параметрических колебаний в линейном контуре
38
