Понижение порядка дифференциального уравнения

До сих пор мы решали только дифференциальные уравнения первого порядка. Существуют дифференциальные уравнения высших порядков, которые сводятся к решению дифференциальных уравнений первого порядка. Простейший пример: . Очевидно, что для получения решениядостаточно дважды проинтегрировать правую часть. Заметим, что при первом интегрировании мы получаем постоянную интегрирования. При втором интегрирование мы снова получаем постоянную интегрирования – уже другую:. Таким образом, решение дифференциального второго порядка содержит уже две произвольные постоянные. Очевидно, что решая подобное простейшее уравнение-го порядка, мы получимпроизвольных постоянных. Следовательно, что для получения частного решения дифференциального уравнения-го порядка следует задаватьдополнительных условий.

1.Уравнение вида . В этом случае следует взять за неизвестную функцию. Найдя, мы определиминтегрированием.

П р и м е р. Решить уравнение . Введем функциюи решим уравнение с разделяющимися переменными. Получив его решение, найдем исходную функцию:.

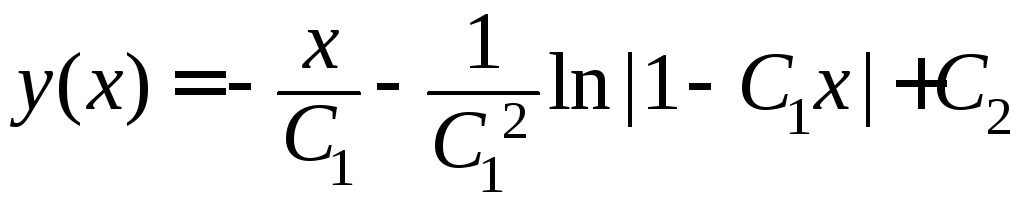Для выделения из множества решений единственного решения можно задать условия:. Например,.

Из последнего условия мы получим , то есть.

Из первого условия получим . Теперь частное решение, удовлетворяющее двум дополнительным условиям, имеет вид

.

2. Уравнение вида . В этом случае целесообразно сделать замену. Заметим, что переменной во введенной функции является не– как в предыдущем случае, а. Теперь. Уравнение становится дифференциальным уравнением первого порядка. Решив его, то есть, найдя, мы получимкак решение уравнения с разделяющимися переменными.

П р и м е р. Решить уравнение . Сделаем заменуи запишем уравнение в виде. Очевидно, что здесь целесообразна еще одна замена:. Уравнение принимает вид линейного уравнения первого порядка:. Решаем сначала соответствующее однородное (), а затем ищем решение неоднородного уравнения в виде. Подставляя в уравнение, получим, и значит,. Следовательно, для определения функциимы имеем уравнения. Это уравнения с разделяющимися уравнениями, и мы должны восстановить первообразные по дифференциалам: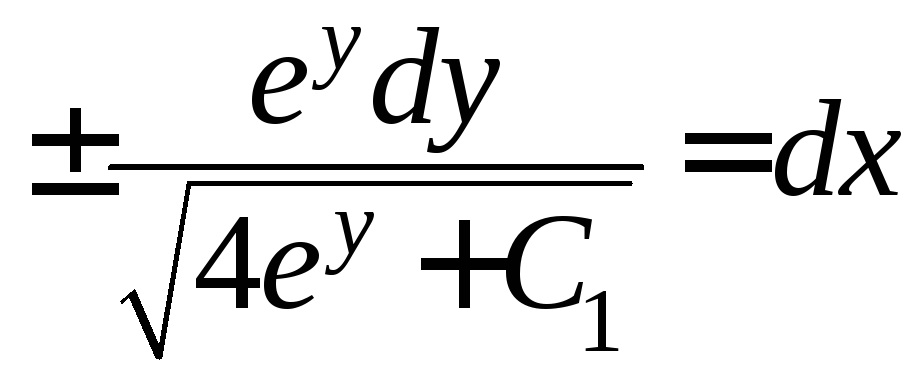. В результате получим решение:.

Для того, чтобы конкретизировать данное решение, то есть, определить значения , недостаточно одного начального условия при решении задачи Коши. В случае дифференциального уравнения второго порядка задача Коши имеет два начальных условия:и.

Для данного примера зададим следующие начальные условия: . Тогда получим. И решение примет видили.

Применение пакета программ maxima для решения задачи Коши в случае дифференциального уравнения второго порядка

Команда ode2 применяется и для решения дифференциальных уравнений второго порядка. В частности, для того, чтобы решить задачу Коши в предпоследнем примере, введем сначала дифференциальное уравнение:

x^2*‘diff(y,x,2)= (‘diff(y,x))^2. Записав его (например, под номером %o1), решим его по команде ode2(%o1,y,x). В данном случае мы задаем два начальных условия, поэтому следующая команда содержит 2 вместо 1. То есть, если решение имеет номер %o2, используем начальные условия по команде ic2(%o2,x=1,y=0,’diff(y,x)=2). Решение задачи Коши будет построено.