Уравнение в полных дифференциалах и приводимое к нему

Уравнение первого порядка , очевидно, может быть записано в виде. Представим теперь, чтои эти функции непрерывны. Это означает, что существует такая функция, что. Действительно, ведь. Итак, уравнение теперь имеет видили. Следовательно, решение исходного уравнения – множество неявно заданных функций.

П р и м е р. Решить уравнение . Мы видим, что условиевыполняется. Перегруппировывая слагаемые в виде, можно заметить, что первая скобка – это. Следовательно, уравнение можно переписать в виде. Следовательно, решением является неявно заданная функция.

Иногда удается найти для произвольного дифференциального уравнения вида такую функцию, что умножив обе части уравнения на эту функцию, мы превращаем его в уравнение в полных дифференциалах, так как. Такой сомножитель называетсяинтегрирующим множителем.

П р и м е р. Решить уравнение . Сгруппируем члены уравнения следующим образом:. Мы видим, что вторая скобка представляет собой. Разделим обе части уравнение на первую скобку: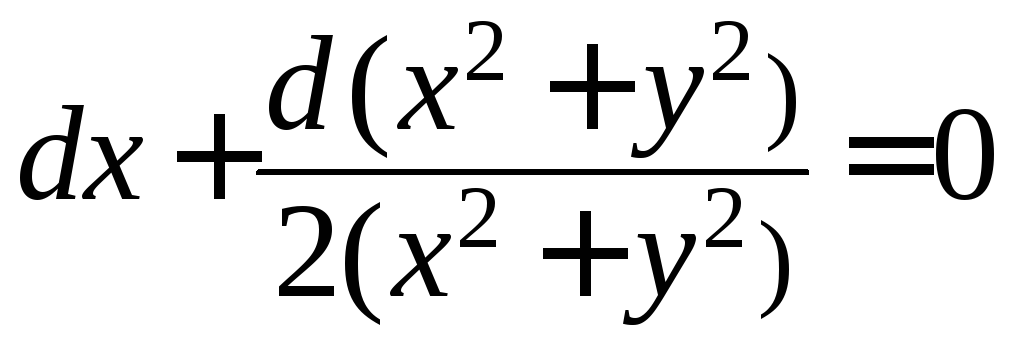или. Отсюда. Здесь интегрирующим множителем явилась функция.

Линейное дифференциальное уравнение первого порядка

Так называется дифференциальное уравнение вида . Здесь сама функция и ее производная связаны линейно. Решать уравнение будем методом вариации произвольной постоянной. Для этого сначала решим соответствующее уравнение с нулевым свободным членом, называемоелинейным однородным уравнением: . Это уравнение является уравнением с разделяющимися переменными и имеет решение. Теперь мы будем искать решение исходного неоднородного уравнения в виде

. Найдем неизвестный множитель , подставивв указанном виде в заданное уравнение. Мы получим.

После взаимного уничтожения одинаковых слагаемых в левой и правой частях придем к соотношению . Отсюда мы найдем, а затем ис точностью до произвольного постоянного слагаемого.

П р и м е р. Найти кривые, у которых площадь трапеции, ограниченной осями координат, касательной и ординатой точки касания, есть величина постоянная, равная .

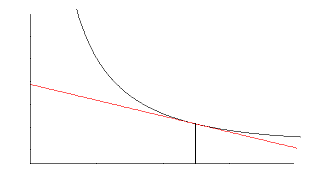
Решение. Высота трапеции равна абсциссе точки касания . Большее основание трапеции отличается от меньшего, равного, на величину. Выражая площадь трапеции, получим соотношение, откуда выведем линейное уравнение. Найдем сначала решение соответствующего однородного уравнения. Это. Теперь подставим выражениев линейное неоднородное уравнение. Мы получим соотношение, откуда. Осталось подставить выражениев представление. В результате получим решение.

Уравнение Бернулли

К решению линейного уравнения сводится решение уравнения Бернулли , где. Действительно, если разделить обе части уравнения на, то становится очевидной необходимость замены. Действительно, уравнение принимает види оказывается линейным уравнением. Решив его и найдя, мы возвращаемся к функциив соответствии с приведенной формулой.

П р и м е р. Решить уравнение . Введем новую функцию. Тогда исходное уравнение сводится к линейному уравнению. Решая соответствующее однородное уравнение, получим, следовательно, решение неоднородного линейного уравнения следует искать в виде. Подставив в уравнение, получимили. В итоге, восстановиви перейдя к, получим.