
Свойства дискретного преобразования Лапласа.
1.Аддитивность:
![]()
2. Однородность:
![]()
3.Теорема
смещения:
![]()
4.Теорема
запаздывания:
![]()
5.Теорема
опережения: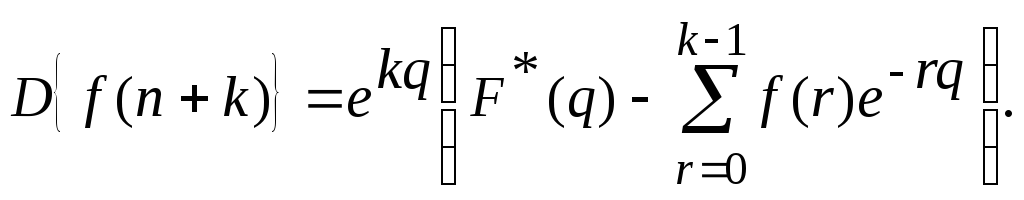
6.Теорема
о свертке:
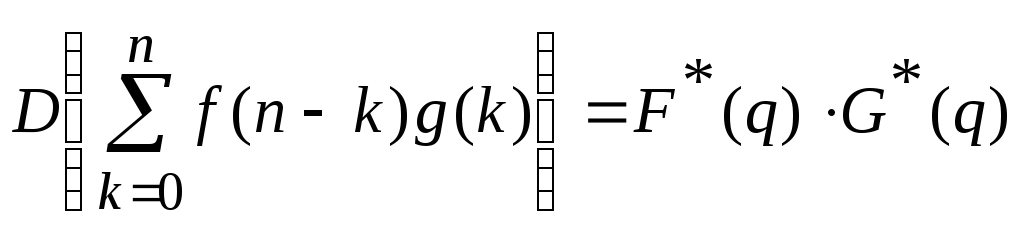 ,
где
,
где
![]() .
.
![]() называется сверткой
решетчатых функций
называется сверткой
решетчатых функций
![]() и
и
![]() .
.
7.Теорема о дифференцировании изображения:
![]() В частности
В частности
![]()
8.Теорема
об интегрировании изображения: если
![]() ,
,
![]() то
то
![]()
В задачах 15.142-15.146 используя теорему об интегрировании изображения, найти изображения следующих функций:
15.142
![]() 15.143
15.143
![]()
15.144
![]() 15.145
15.145
![]() 15.146
15.146
![]()
В задачах 15.147-15.148 используя теорему запаздывания, найти изображения следующих функций:
15.147
![]() 15.148
15.148
![]()
В задачах 15.149-15.150 используя теорему опережения, найти изображения следующих функций:
15.149
![]() 15.150
15.150
![]()
В задачах 15.151-15.158 используя таблицу изображений дискретного преобразования Лапласа, найти оригиналы следующих изображений:
15.151![]() 15.152
15.152![]()
15.153![]() 15.154
15.154![]() 15.155
15.155![]() 15.156
15.156
![]() 15.157
15.157
![]() 15.158
15.158
![]()
В задачах 15.159-15.160 используя теорему о свёртке найти оригиналы для следующих изображений:
15.159
![]() 15.160
15.160
![]()
§4. Z – преобразование.
![]() -преобразованием
решетчатой функции
-преобразованием
решетчатой функции
![]() называется функция
называется функция
![]() комплексного переменного
комплексного переменного
![]() ,
определяемая равенством:
,
определяемая равенством:
![]() .
При этом
функция
.
При этом
функция
![]() называется оригиналом,
а функция
называется оригиналом,
а функция
![]() - его изображением.
Соответствие между оригиналом и его
изображением символически записывается
в виде
- его изображением.
Соответствие между оригиналом и его
изображением символически записывается
в виде
![]() или
или
![]() .
.
Таблица изображений Z - преобразования.
|
|
|
|
|
1. |
1 |
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|
|
11. |
|
|
|
12. |
|
|
|
13. |
|
|
|
14. |
|
|
Свойства z - преобразования.
1.Аддитивность:
![]() .
.
2.Однородность:
![]()
3.Теорема
смещения:
![]()
4.Теорема
запаздывания:
![]()
5.Теорема опережения:
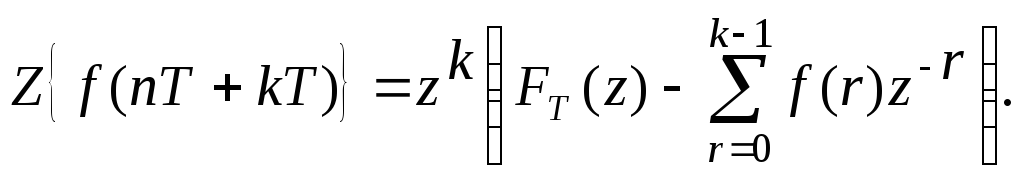
6.Теорема
о свертке: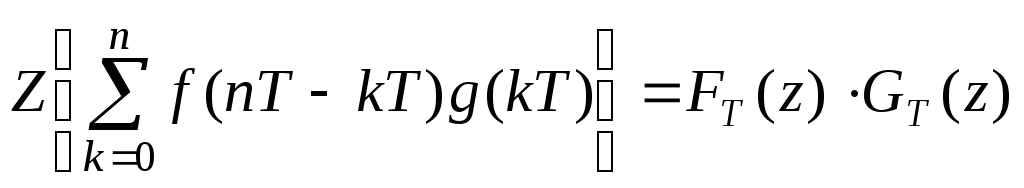 ,
,
где
![]()
7.Теорема о дифференцировании изображения:
![]()
В задачах 15.161-15.170 используя таблицу изображений Z-преобразования, найти изображения следующих функций:
15.161
![]() 15.162
15.162![]() 15.163
15.163
![]() 15.164
15.164
![]()
15.165
![]() 15.166
15.166
![]() 15.167
15.167
![]()
15.168
![]() 15.169
15.169
![]() 15.170
15.170
![]()
В задачах
15.171-15.180 найти
Z-изображение
непрерывной функции, заданной её
изображением Лапласа, в дискретных
точках с периодом дискретности
![]() :
:
15.171
![]() 15.172
15.172
![]() 15.173
15.173
![]() 15.174
15.174
![]() 15.175
15.175
![]() 15.176
15.176
![]()
15.177
![]() 15.178
15.178
![]() 15.179
15.179
![]() 15.180
15.180
![]()
Ответы к главе 1.
1.1 18
1.2
![]() 1.3
1 1.4
1.3
1 1.4
![]() 1.5
0 1.6 0
1.7 1
1.8
1 1.9
1.5
0 1.6 0
1.7 1
1.8
1 1.9
![]()
1.10
![]() 1.13
0 1.14
0 1.15
0 1.16
0 1.18
1.13
0 1.14
0 1.15
0 1.16
0 1.18
![]() 1.19
1.19
![]() 1.20
4 1.21
0
1.20
4 1.21
0
1.22
![]() 1.23
1.23
![]() 1.24
0
1.24
0
1.25 48 1.26 223 1.27 900 1.28 394 1.29 665
1.30
![]() 1.31
1.31 1.32а)
1.32а)![]() б)
б)![]()
1.33а)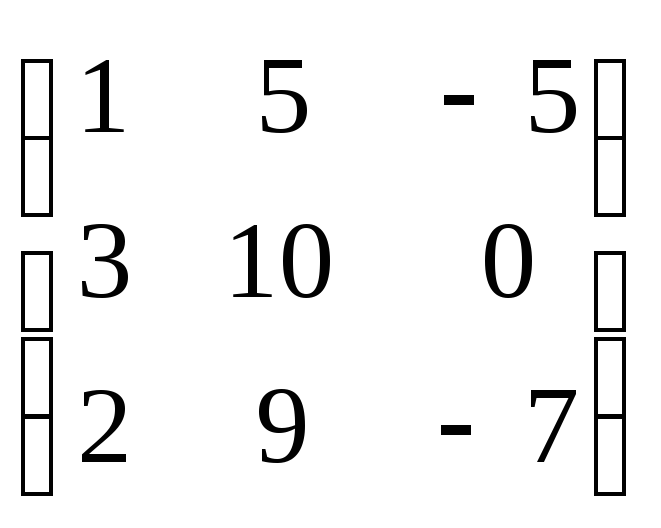 б)
б)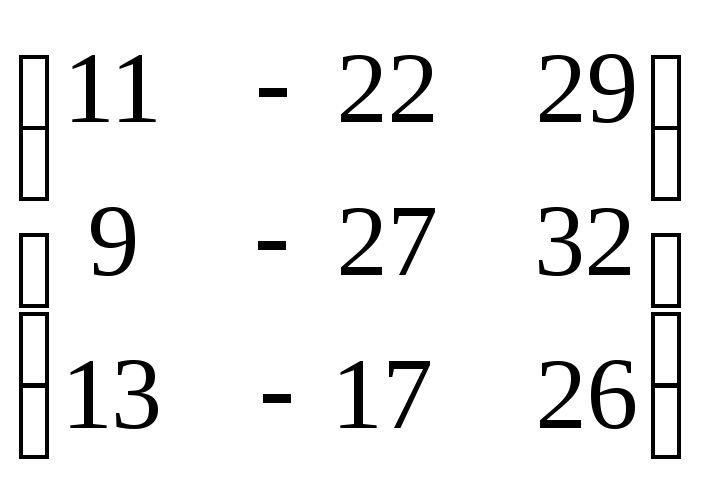 1.34 а)
1.34 а)![]() б)
б)
![]()
в)
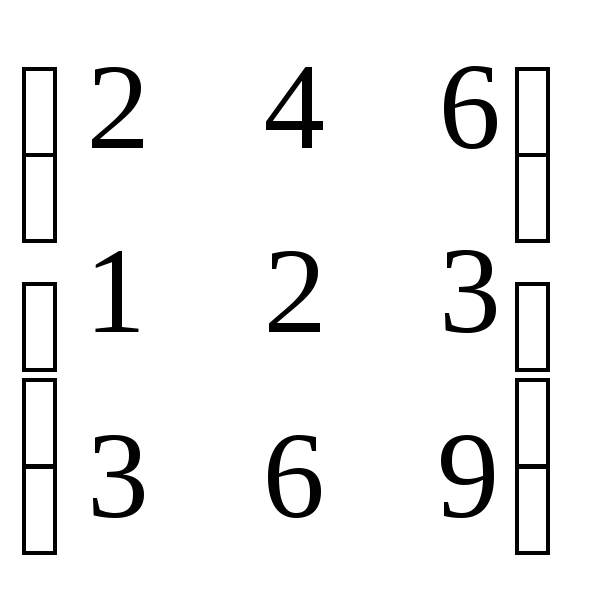 г) (13)
1.35 а)
г) (13)
1.35 а)![]() б)
б)![]()
1.36 а)
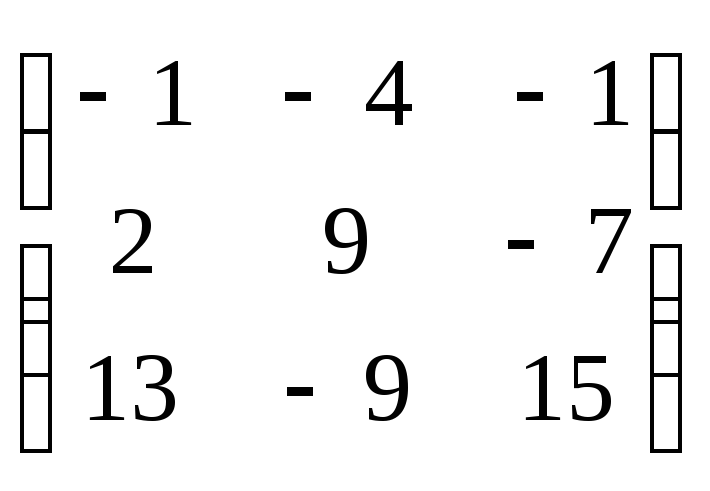 б)
б)
1.37а)
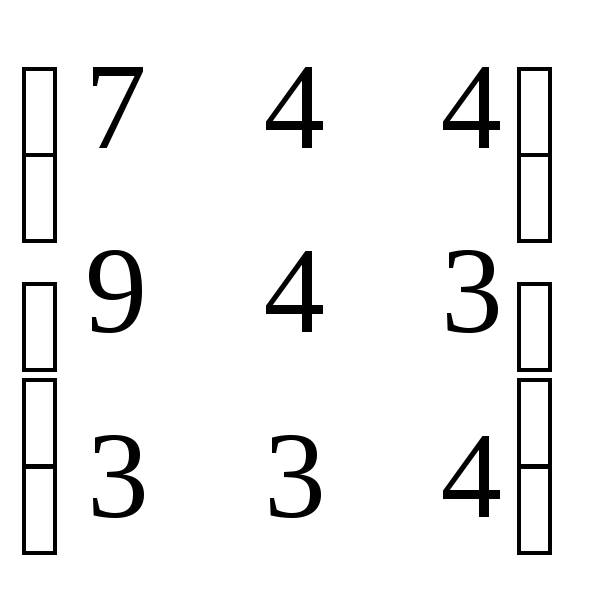 б)
б)![]() 1.38
1.38
![]() 1.39
1.39
![]()
1.40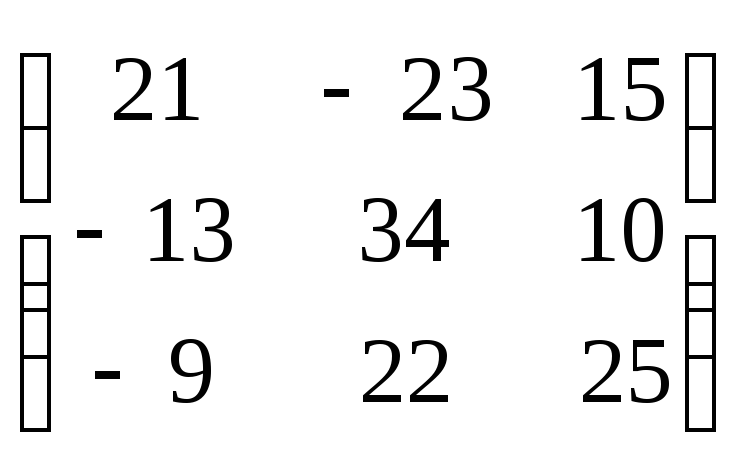 1.41
1.41![]() 1.42
1.42 1.43
1.43![]()
1.44 1.45
1.45![]() 1.46
1.46![]()
