§ 2. Приложения операционного исчисления.

Для нахождения решения линейного дифференциального уравнения с постоянными коэффициентами , удовлетворяющего начальным условиям , , , , к обеим частям уравнения следует применить преобразование Лапласа и перейти к операторному уравнению , где - изображение искомого решения , - изображение функции , - некоторый многочлен, коэффициенты которого зависят от начальных данных ,,, (, если ). Решив операторное уравнение относительно : и найдя оригинал для , получим искомое решение . Если начальные данные ,,, считать произвольными постоянными , то найденное решение будет являться общим решением данного дифференциального уравнения.

Системы линейных дифференциальных уравнений с постоянными коэффициентами решаются аналогично. Отличие состоит лишь в том, что вместо одного операторного уравнения получится система операторных уравнений, линейных относительно изображений искомых функций.

В задачах 15.81-15.86 найти общие решения следующих дифференциальных уравнений:

15.81 15.82

15.83 15.84

15.85 15.86

В задачах 15.87-15.100 найти частные решения дифференциальных уравнений при указанных начальных условиях:

15.87 , . 15.88 , .

15.89 .

15.90 .

15.91 .

15.92 .

15.93 .

15.94 .

15.95 .

15.96 .

15.97 , , где

15.98 , , где

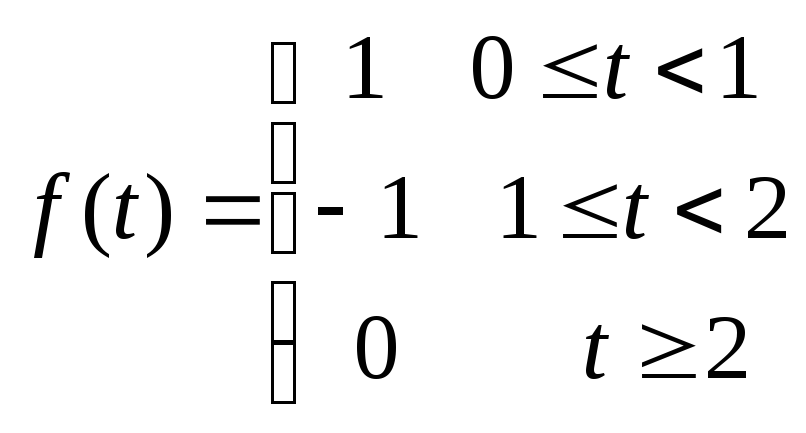
15.99 , , где

15.100 ,, где

В задачах 15.101-15.112 найти частные решения систем дифференциальных уравнений для указанных начальных условий:

15.101

15.102

15.103

15.104

15.105

15.106

15.107 , .

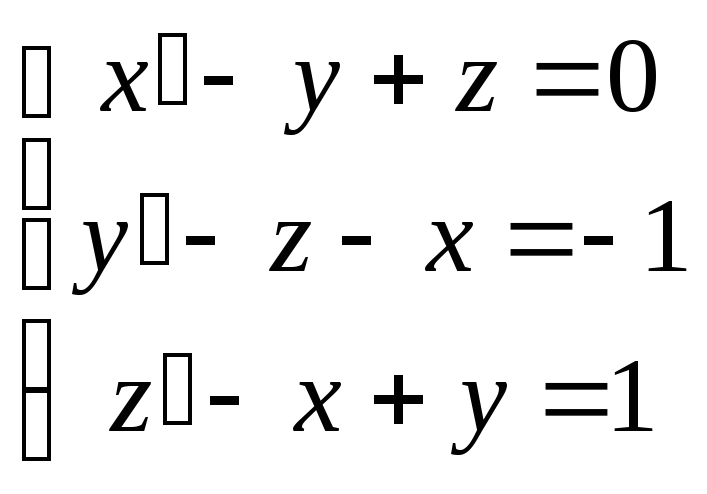
15.108 , .

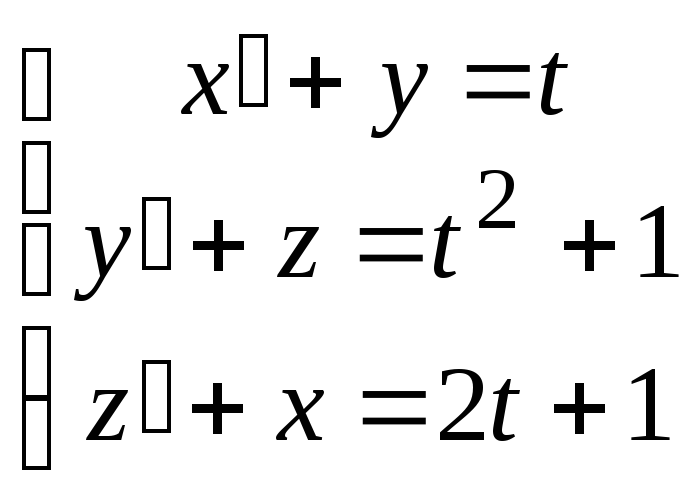
15.109 , .

15.110

15.111 ,

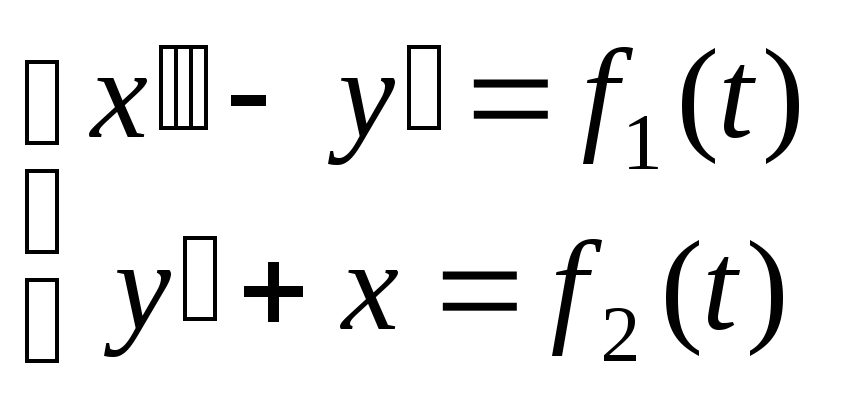где и

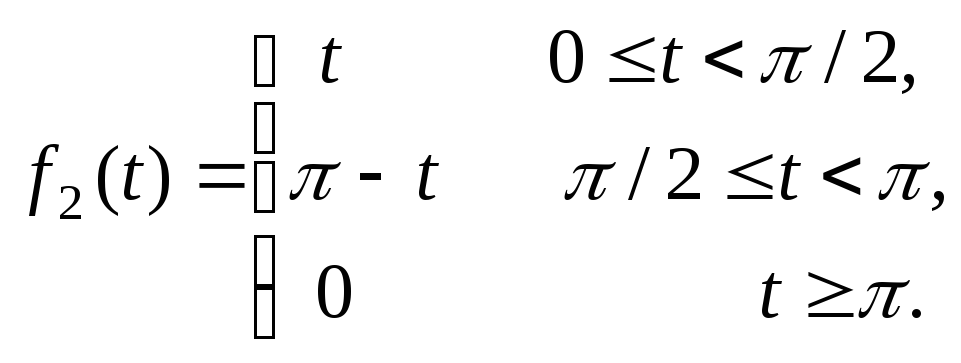
15.112

где

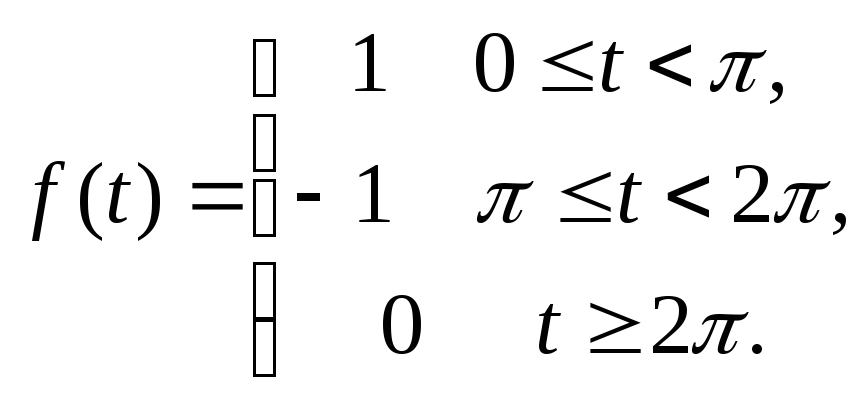
Для нахождения решений линейных интегральных и интегро-дифференциальных уравнений, используя теорему о свёртке, находят сначала изображения искомых решений этих уравнений, а затем и само решение.

В задачах 15.113-15.120 найти решения следующих интегральных уравнений:

15.113 15.114

15.115 15.116

15.117 15.118

15.119 15.120

В задачах 15.121-15.125 найти решения интегро-дифференциальных уравнений для указанных начальных условий:

15.121 , .

15.122 , .

15.123 , .

15.124 ,

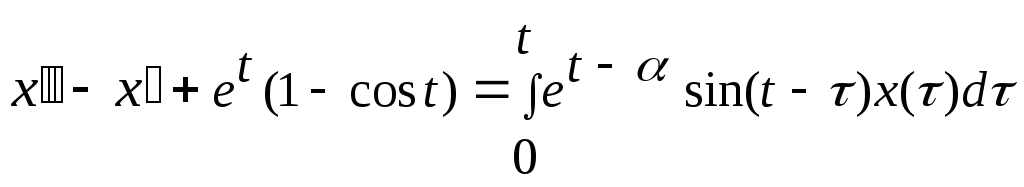15.125 , .

§ 3. Дискретное преобразование Лапласа.

Функцию , определённую только в некоторых точках числовой прямой называют решетчатой. Будем в дальнейшем рассматривать решетчатые функции, определённые в равноотстоящих точках , где - целое число, - постоянная, называемая периодом дискретности. Решетчатые функции обозначают , а если , то .

Решетчатая функция такая, что: 1) при ; 2) существуют положительные числа и такие, что для всех справедливо неравенство , называется дискретным оригиналом.

Дискретным преобразованием Лапласа функции называется функция комплексного переменного , , определяемая равенством: . При этом функция называется оригиналом, а функция - его изображением. Соответствие между оригиналом и его изображением символически записывается в виде или .

Часто дискретное преобразование Лапласа рассматривают для случая , при этом .

В задачах 15.126-15.133 используя таблицу изображений дискретного преобразования Лапласа, найти изображения следующих функций:

15.126 15.127 15.128 15.129

15.130 15.131

15.132 15.133

В задачах 15.134-15.135 используя теорему смещения найти изображения следующих функций:

15.134 15.135

В задачах 15.136-15.141 используя теорему о дифференцировании изображения, найти изображения функций:

15.136 15.137 15.138

15.139 15.140 15.141

Таблица изображений дискретного преобразования Лапласа.

1.	1
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.