Векторная алгебра

Векторным произведением двух векторов называется третий вектор, длина которого равна произведению модулей перемножаемых векторов на синус угла между ними, направлен этот вектор перпендикулярно плоскости, в которой расположены перемножаемые векторы, образуя с ними правую тройку.

Обозначения векторного произведения или .

Свойства векторного произведения

1. . Доказательство этого свойства следует из того, что если поворот от к с некоторой точки виден против часовой стрелки, поворот от к с этой же точки, очевидно, видится по часовой стрелке, то есть направление векторного произведения по сравнению с меняется на противоположное, что и доказывает свойство.

2. , где число.

3. .

4. , если и коллинеарны. Доказательство следует из того, что между коллинеарными векторами угол 0 или , но .

Векторное произведение векторов в ортонормированном базисе

Если , , векторное произведение векторов вычисляется с помощью формулы

.

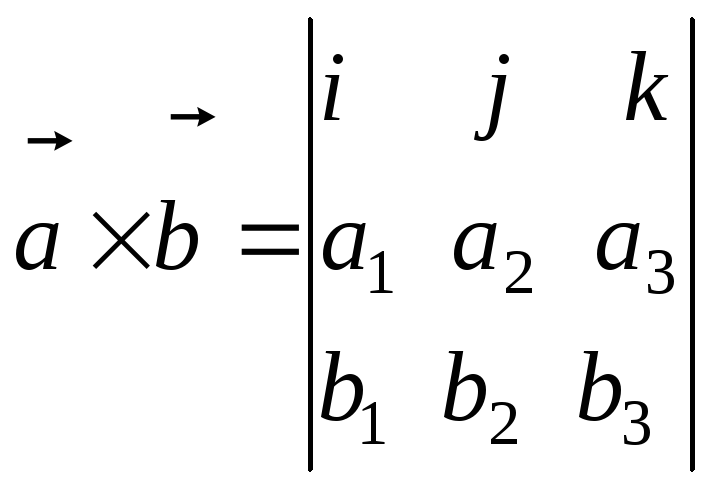Доказательство.

Рассмотрим векторные произведения базисных векторов.

как произведения коллинеарных векторов, , в самом деле, , то есть равен длине вектора , и тройка векторов - правая. Из первого свойства векторного произведения следует . Аналогично . Действительно длина векторного произведения равна единице, как и длина вектора , с конца вектора кратчайший поворот от вектора к вектору видится против часовой стрелки, что следует из рисунка 7. Из первого свойства имеем . Так же доказывается, что .

Вычислим

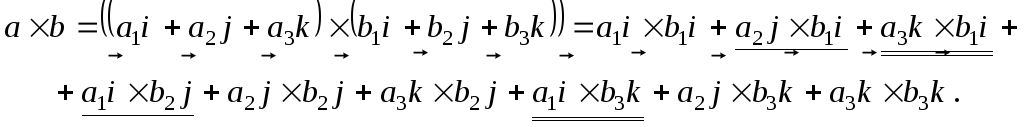
Этот результат следует из 3 – го свойства скалярного произведения.

Очевидно первое, пятое и девятое слагаемые в правой части формулы равны нулю как произведения коллинеарных векторов.

Далее

,

,

.

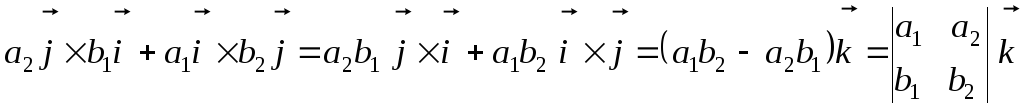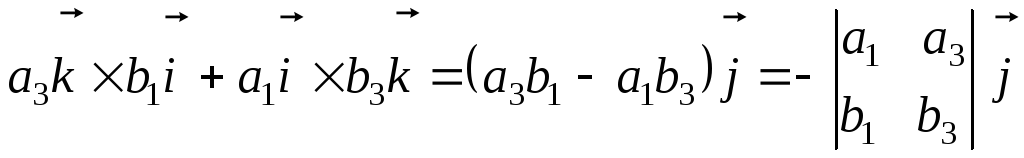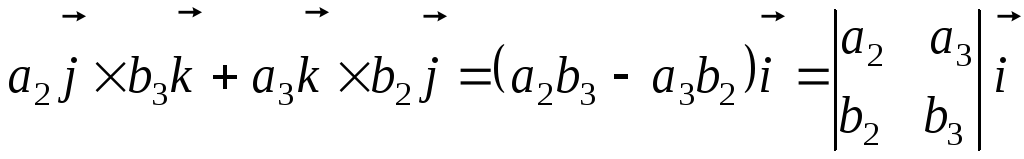Итак,

,

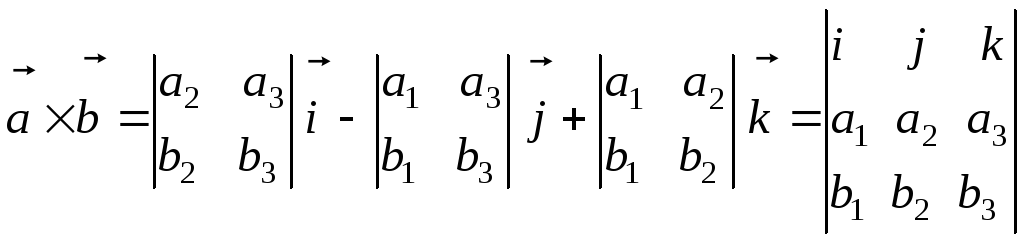что и требовалось доказать.

Замечание 1. Определитель третьего порядка в этой формуле называют иногда символическим, поскольку не все свойства обычных определителей для него справедливы. Это связано с тем, что одна из строк состоит из векторов, элементы двух других - скаляры. Его использование оправдано тем, что после записания векторного произведения его легко представить в обычном виде, разложив определитель по элементам, скажем, первой строки.

Замечание 2. Условием коллинеарности векторов является равенство нулю их векторного произведения. Следовательно, символический определитель должен быть равен нулю, для этого достаточно, чтобы любые две его строки, или два столбца были пропорциональны. Столбцы пропорциональными быть не могут, так как базисные векторы не коллинеарны, а значит не пропорциональны, строка из векторов не может быть пропорциональна строке из скаляров по той же причине. Остается пропорциональность двух последних строк определителя. Итак, условием коллинеарности векторов , является

.

Пример.

Определить площадь треугольника, заданного вершинами , .

Поскольку площадь параллелограмма, построенного на векторах , равна , то есть длине векторного произведения этих векторов, площадь заданного треугольника равна половине площади параллелограмма, то .

Вычислим

.

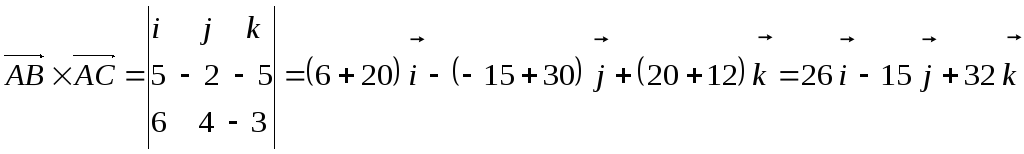В итоге .

Смешанное произведение трех векторов

Смешанным произведением трех векторов называется число, равное векторному произведению , умноженному скалярно на вектор , то есть .

Модуль смешанного произведения равен объему параллелепипеда построенного на этих векторах. Если векторы компланарны, то смешанное произведение , что следует из определений векторного, скалярного и смешанного произведений.

Для векторов , , ,

смешанное произведение определяется формулой

.

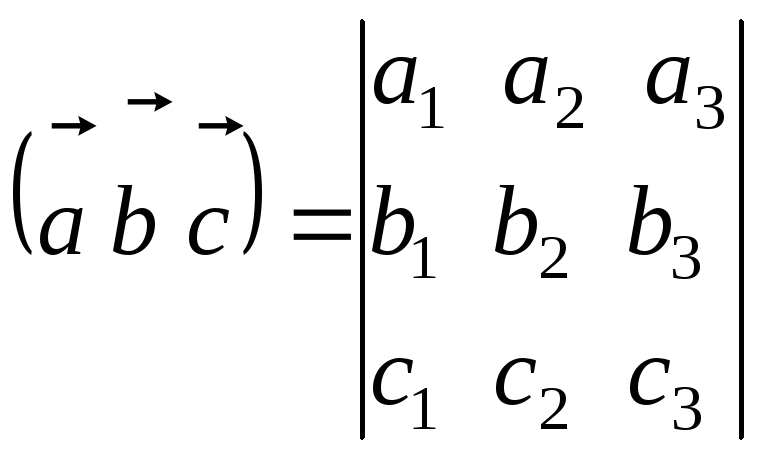Доказательство. Так как ,

.

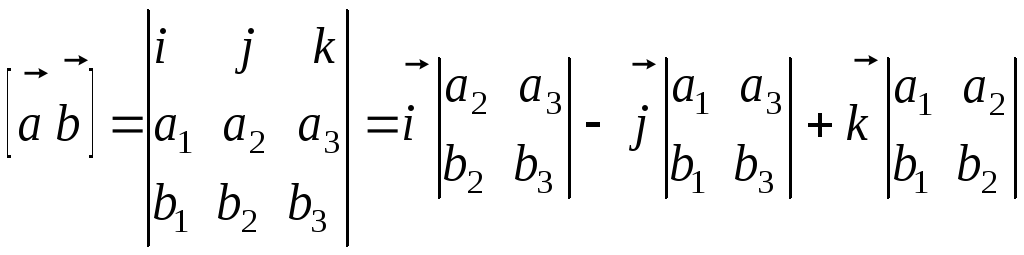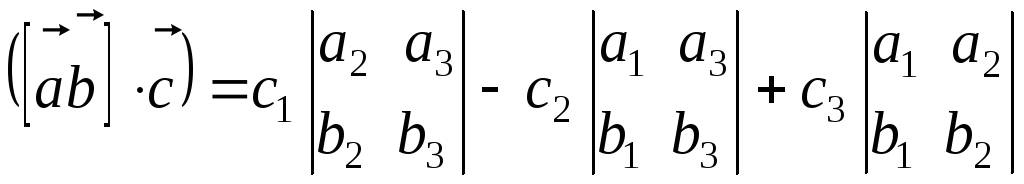Правая часть последней формулы является разложением приведенного выше определителя по элементам третьей строки, что доказывает формулу.

Пример.

Вычислить объем параллелепипеда, заданного векторами , , .

Вычислим ,

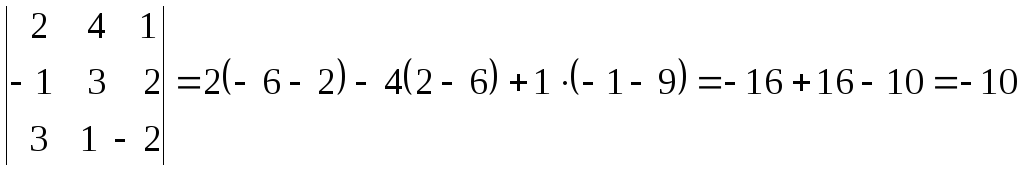Объем этого параллелепипеда равен 10.

Примеры для самоподготовки.

6.1. Вычислить вектор , если , .

.

6.2. Определить скалярное произведение векторов , если , угол между ними ? .

6.3 Определить скалярное произведение векторов , . .

6.4. Определить длину векторного произведения векторов и

. .

6.5. Определить длину векторного произведения , если , угол между ними . .

6.6 Установить, при каком значении векторы , ортогональны? .

6.7. Проверить коллинеарность векторов , .

6.8. Проверить при каком векторы , , компланарны? .