Лекция 3 Принципы решения прямых и обратных задач гравиразведки

1. Аналитические способы решения прямых задач гравиразведки

2. Прямая и обратная задачи над шаром

3. Прямая и обратная задачи над горизонтальным бесконечно длинным круговым цилиндром

4. Прямая и обратная задача над вертикальным уступом (сбросом)

5. Графическое определение аномалии силы тяжести двухмерных тел с помощью палетки Гамбурцева

6. Плотность горных пород

Аналитические способы решения прямых задач гравиразведки

Аномалия силы тяжести, вызванная притяжением тел известной формы, размера и плотности, может быть вычислена на основании закона всемирного притяжения (закон Ньютона).

Пусть в координатной системе xyz ось z направлена вниз к центру Земли. Ставится задача определить в точке наблюдения А(x,y,z) аномальную силу тяжести (Δg), т.е. вертикальную составляющую силы притяжения Землей единицы массы (m_A = 1 ) элементарной массой dm, находящейся в точке M (x',y',z').

По закону Ньютона притяжение единичной массы равно:

(1)

где: f – гравитационная постоянная, r – расстояние между точками А и М.

Аномалия Δg является проекцией вектора F на ось z:

(2)

потому, что из треугольника АВМ cosα = (z’ – z)/r.

Это же выражение можно получить с помощью потенциала W=fdm/r. Т.к. Δg = - ∂W/∂z, а r = [(x’-x)²+(y’-y)²+(z’-z)²]^1/2. Следовательно,

Δg = - ∂(fdmr ^-1)/∂z = fdmr ^-2_*(∂r/∂z) = - fdmr ^-2_*(1/2r)_*(∂[(z’-z)²]/∂z) =

- fdmr ^-2_*(1/2r)_*2(z’-z)*[∂(-z)/∂z] = fdm_*(z’-z) / r³.

Обозначив плотность притягивающей массы через σ, а ее объем черех dV, можно записать:

(3)

Такова будет аномалия силы тяжести, обусловленная массой, расположенной в пустоте. В природных условиях аномальные включения расположены во вмещающей среде с некоторой плотностью σ₀, поэтому под массой dm надо понимать избыточную массу dm = (σ – σ₀)dV. Отсюда:

(4)

где (σ – σ₀) = Δσ – избыточная плотность. При σ > σ₀ Δg имеет положительный знак, т.е. наблюдается увеличение притяжения и положительные аномалии Δg. При σ < σ₀ Δg имеет отрицатель­ный знак, т.е. наблюдается уменьшение притяжения и отрицательные анома­лии Δg. При σ = σ₀ аномалия Δg отсутствует.

В принципе аномалия, созданная любым телом, может быть определена интегралом по объему тела: (5)

т.е. суммой притяжений всех элементарных объемов, из которых состоит тело.

Прямая и обратная задачи над шаром.

1. Прямая задача. Пусть однородный шар радиуса a и плотности σ расположен на глубине h в среде с плотностью σ₀ (для простоты центр шара находится на оси z, а наблюдения проводятся по оси x в точке P).

Ф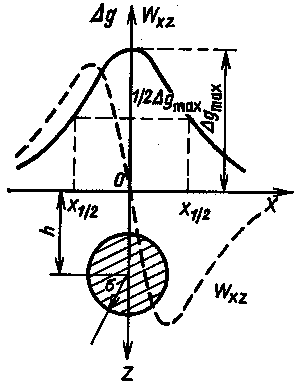ормула для вычисления g может быть получена из (4) путем замены эле­мента dm массой шара в силу того, что притяжение однородным шаром проис­ходит так, как если бы вся масса была сосредоточена в центре шара. Учтя, что x'=y'=0, z'=h, y=z=0, полу­чим для шара:

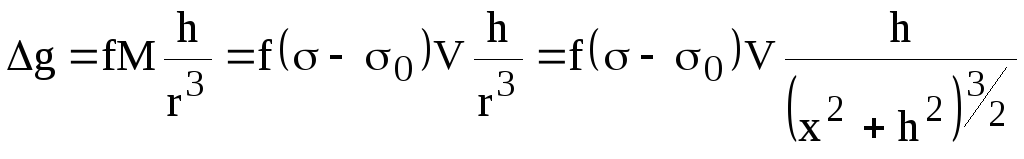(6)

График Δg будет иметь максимум над шаром (x=0) и асимптотически стремиться к нулю при удалении от шара. В плане изолинии Δg будут иметь вид концентрических окружностей.

Вторая производная (градиент аномалии по профилю наблюдений) равна:

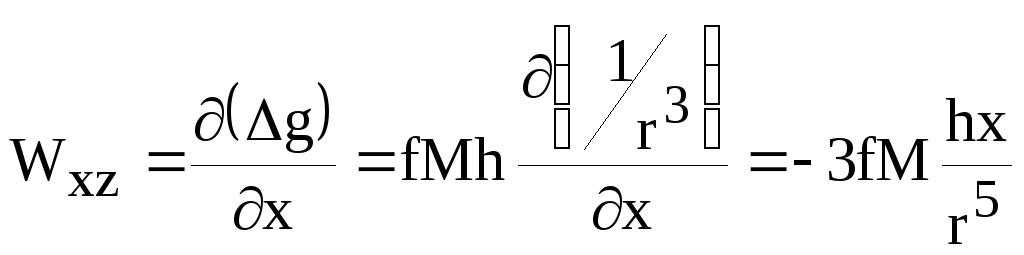(7)

Вид кривой W_xz может быть легко получен путем графического построения из кривой Δg. График W_xz имеет перед шаром максимум, за шаром - минимум, над центром шара - ноль.

2. Обратная задача. Из (6) максимум Δg над центром шара (x=0) равен

(8)

Для точки, удаленной от максимума на расстояние x_1/2, имеющей Δg_1/2 = 0.5_* Δg_max, можно записать следующее уравнение:

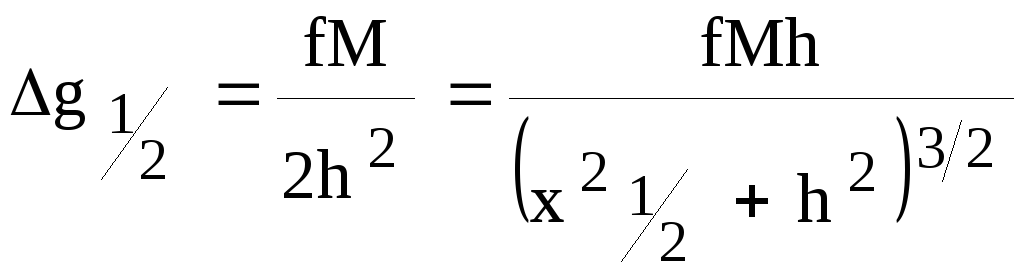или (9)

Решив последнее уравнение, получим формулу для определения глубины залегания центра шара h=1,3x_1/2. Зная h, легко найти избыточную массу (M): M = Δg _maxh²/f. Так как M = V(σ – σ₀) = (4/3)_*πa³_*( σ – σ₀) то, зная избыточную плотность σ – σ₀), можно рассчитать объем (V) и радиус шара (a). Так, радиус равен:

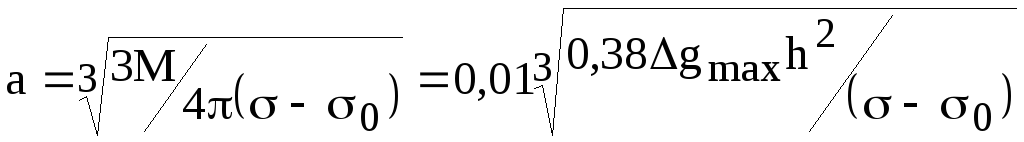(10)

где Δg _max- в миллигалах, h - в метрах, σ – σ₀) - в т / м³ (г/см³).

Прямая и обратная задачи над горизонтальным бесконечно длинным круговым цилиндром.

1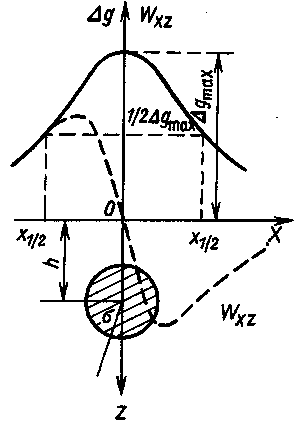.Прямая задача. Рассмотрим бесконечно длинный круговой горизонта­ль­ный цилиндр радиуса R, расположенный вдоль оси y. Ось наблюдений ( x) направим вкрест простирания цилиндра.

Притяжение однородным цилиндром происходит так же, как если бы вся его масса была сосредоточена вдоль вещественной линии, расположенной вдоль оси цилиндра, с массой единицы длины, равной λ = dm/dy = πR²(σ – σ₀). Используя (5), можно получить формулы для Δg и W_xz:

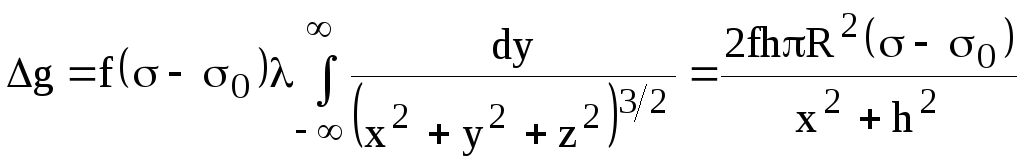(11)

(12)

Графики Δg и W_xz над цилиндром и шаром внешне похожи. В плане изоли­нии Δg над цилиндром будут вытянутыми параллельными линиями.

2. Обратная задача. Из (11) можно при х=0 получить Δg _max = 2fλ/h. Отсюда

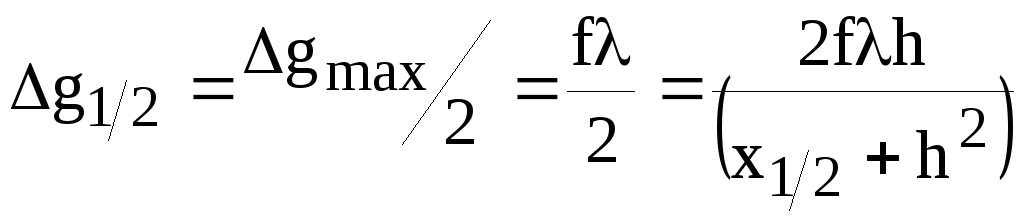(13)

и h² = x²_1/2, h = x_1/2, т.е. глубина залегания цилиндра равна расстоянию от точки максимума Δg _max до точки, где Δg = Δg _max/2.

Определив h и зная избыточную плотность, можно рассчитать

(14)

и радиус цилиндра:

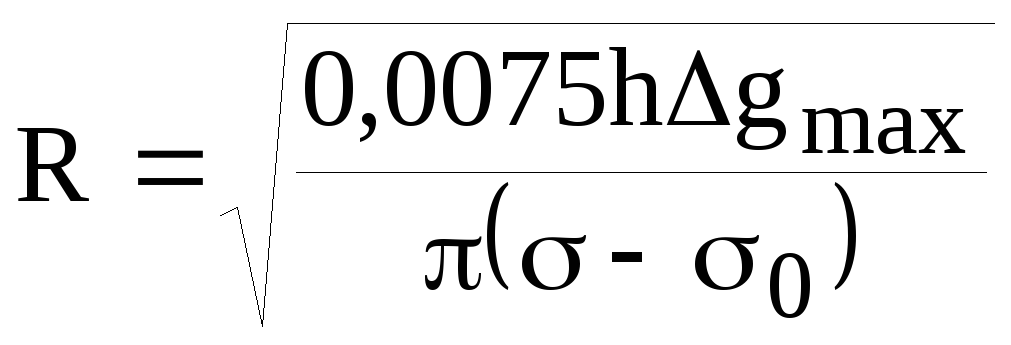(15)

Зная R, можно получить глубины залегания верхней h_B = h - R и нижней h_н = h+R кромок цилиндра. Нетрудно вычислить выражение и для W_xz.

Прямая и обратная задача над вертикальным уступом (сбросом).

1. Прямая задача. Пусть вертикальный уступ (сброс) простирается бесконечно вдоль оси y.

Н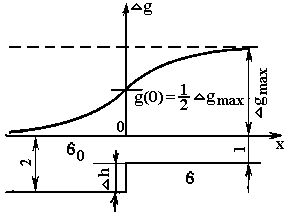аблюдения производятся вдоль оси x, ( y=z=0), расположенной вкрест простирания сброса. Если глубина до кровли z1 и z2 , а амплитуда уступа h, то, согласно (5), значения Δg в каждой точке по оси х будут описываться следующим выражением:

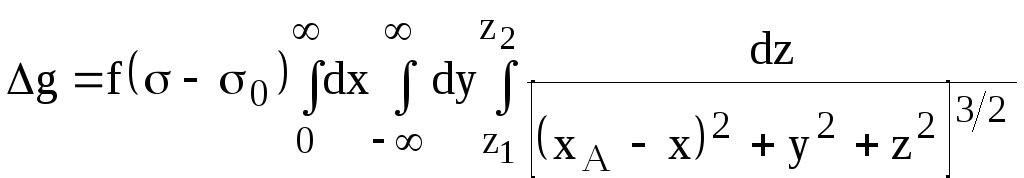(16)

где координаты с индексом относятся к точкам наблюдения, а координаты без индекса – к уступу.

В общем случае выражение интеграла имеет громоздкий вид. В частности, полная максимальная аномалия над уступом (разность силы тяжести между поднятым и опущенным крылом) определится следующей формулой:

(х = ∞) (17а)

Δg = 0 (х = -∞) (17б)

(х = 0) (17в)

2. Обратная задача. Из (17а) можно определить

В теории гравиразведки доказано, что примерная глубина расположе­ния середины высоты уступа H = (z₂ + z₁)/2 равна x_1/2, т.е. абсциссе точки, в которой Δg_1/2 = Δg₀/2 = Δg_max/4, где Δg₀ - аномалия над уступом, а Δg max - полная аномалия. Практически для определения H на кривой Δg находится местоположение сброса (Δg₀) и в масштабе профиля рассчитывается x_1/2 - расстояние от сброса до точки, в которой Δg = Δg₀/2. Зная H и h, легко определить глубины до приподнятого (z₁ = H – h/₂) и опущенного (z₂ = H + h/₂) крыла.