Лекция 3

Связь криволинейного интеграла второго рода по замкнутой кривой в пространстве с поверхностным интегралом. Формула Стокса.

Пусть C – гладкая замкнутая пространственная кривая, S – такая двусторонняя поверхность, что кривая C является границей этой поверхности. Тогда справедлива формула Стокса

, (ФС)

где выбор стороны поверхности, а значит, выбор знаков направляющих косинусов нормали к поверхности определяется заданием обхода по кривой C следующим образом: если глядеть с конца вектора нормали к поверхности C, должно быть видно, что обход кривой C совершается против часовой стрелки.

Следует пояснить, что собой представляет правая часть формулы Стокса. Под интегралом находится определитель, в верхней строке которого расположены направляющие косинусы вектора нормали к поверхности S, в средней строке расположены символические операторы нахождения частных производных, и в нижней строке расположены функции, представленные в криволинейном интеграле. Раскладывая определитель по верхней строке, мы получим поверхностный интеграл второго рода. Формальное «умножение» символического оператора на функцию означает, что от этой функции следует взять частную производную по соответствующей переменной.

Приведем другое представление правой части формулы Стокса в виде поверхностного интеграла второго рода по координатам:

.

Нетрудно заметить, что в том случае, когда кривая C расположена в плоскости XOY, и в качестве S мы выберем плоскую область, ограниченную кривой C, формула Стокса превращается в уже известную формулу Грина.

Для доказательства параметризуем поверхность S:

, . Будем считать функции дважды непрерывно дифференцируемыми в области значений параметров . Таким образом, благодаря параметризации мы перешли от поверхности S к области , находящейся в параметрической плоскости. Граница C поверхности S соответствует границе области , которую мы назовем . Посчитаем первое слагаемое в криволинейном интеграле с применением введенной параметризации и формулы Грина для интеграла по замкнутой кривой в параметрической плоскости.

Аналогично доказывается, что и .

Сложив все левые и все правые части полученных соотношений, мы получим формулу Стокса.

Благодаря формуле Грина мы получали условие независимости криволинейного интеграла на плоскости от пути интегрирования. Подобным образом, применяя формулу Стокса, можно получить условия независимости криволинейного интеграла в трехмерном пространстве от пути интегрирования. Эти условия имеют вид: .

Связь интеграла по замкнутой поверхности с тройным интегралом по телу, ограниченному этой поверхностью. Формула Гаусса-Остроградского.

Пусть S – двусторонняя замкнутая поверхность, ограничивающая тело V. Предположим, что функции имеют непрерывные частные производные в V и непрерывны на S. Докажем справедливость формулы Гаусса-Остроградского:

, (ФГО)

где поверхностный интеграл взят по внешней стороне поверхности S.

Доказывать формулу Гаусса-Остроградского будем отдельно для каждого слагаемого в подынтегральном выражении.

Докажем, что .

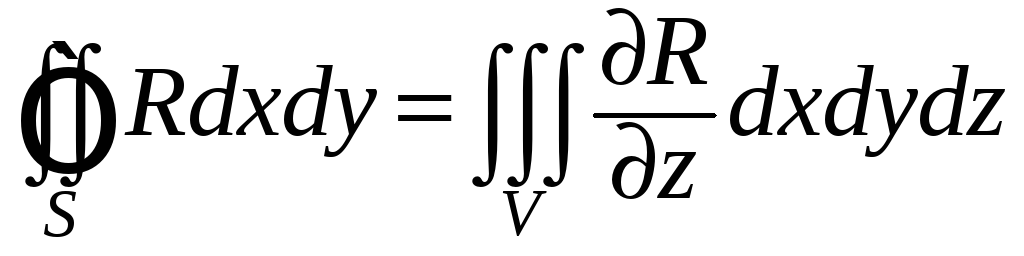1. Сначала представим, что поверхность S либо пересекается любой прямой, параллельной оси OZ не более, чем в двух точках, либо отрезок этой прямой принадлежит S.

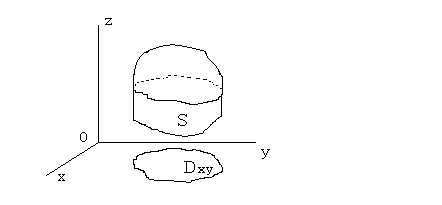
В этом случае поверхность S проецируется на область на плоскости XOY и можно параметризовать S следующим образом: , где . При этом та часть поверхности S, которая содержит отрезки прямых, параллельных оси OZ (обозначим ее ), проецируется на граничные точки . Интеграл по этой части поверхности равен нулю. Учитывая, что поверхностный интеграл взят по внешней стороне поверхности, получим , что дает

2. Для того, чтобы доказать формулу в общем случае, разобьем тело V поверхностями, параллельными оси OZ, на конечное число тел , с граничными поверхностями , удовлетворяющими требованиям предыдущего пункта. Для каждого из полученных тел и соответствующих граничных поверхностей формула Гаусса-Остроградского справедлива. Поскольку интегралы по поверхностям, параллельным оси OZ и входящим в качестве слагаемых в интегралы по поверхностям , равны нулям, получим ,

что и требовалось доказать.

Соотношения и доказываются аналогично. Таким образом, справедливость формулы Гаусса-Остроградского доказана.

НЕСОБСТВЕННЫЙ ДВОЙНОЙ ИНТЕГРАЛ ПО НЕОГРАНИЧЕННОЙ ОБЛАСТИ

Пусть – неограниченная область в плоскости XOY, ее граница проходит через бесконечно удаленную точку (например, полуплоскость или внутренняя часть области, ограниченной двумя лучами с общей вершиной. Пусть функция определена и непрерывна в любой внутренней точке области . Что мы будем понимать под ? Естественно, что введенное выше определение двойного интеграла здесь невозможно, так как невозможно разбить неограниченную область на конечное число ограниченных квадрируемых подобластей, да еще и менять разбиения так, чтобы диаметры подобластей стремились к нулю.

Назовем исчерпанием области последовательность подобластей , , таких, что , каждая область ограничена и квадрируема, и для любой точки найдется номер такой, что . Таким образом, с увеличением номера подобласти , расширяясь, все более приближаются к области . В качестве примера можно рассмотреть в качестве области верхнюю полуплоскость, а в качестве последовательности подобластей – последовательность лежащих в верхней полуплоскости полукругов, опирающихся на отрезки как на диаметры.

Построив исчерпание, рассмотрим последовательность . Если существует , причем при любом другом исчерпании области предел будет таким же, то назовем несобственным двойным интегралом по неограниченной области.

П р и м е р. Исследовать сходимость , где – вся плоскость XOY. Будем исчерпывать плоскость кругами , где n –натуральное число. Для вычисления двойного интеграла по каждому из кругов удобно перейти к полярным координатам по формулам Тогда

Очевидно, что при предел существует, при предел бесконечен. Можно показать, что при предел не зависит от способа исчерпания. Поэтому рассмотренный несобственный интеграл сходится при и расходится при .

Для введенных кратных несобственных интегралов от положительных функций справедливы теоремы сравнения: а) если сходится интеграл от большей функции, то сходится интеграл от меньшей функции, б) если существует конечный предел , то из сходимости следует сходимость .

П р и м е р. Доказать, что интеграл сходится.

Найдем с применением правила Лопиталя

.

В соответствии со второй теоремой сравнения из сходимости следует сходимость .

Применим полученные сведения для вычисления важного интеграла . Для этого вычислим интеграл двумя способами: а) с помощью исчерпания плоскости кругами с увеличивающимися радиусами и б) с помощью исчерпания плоскости квадратами с увеличивающимися длинами сторон.

а) .

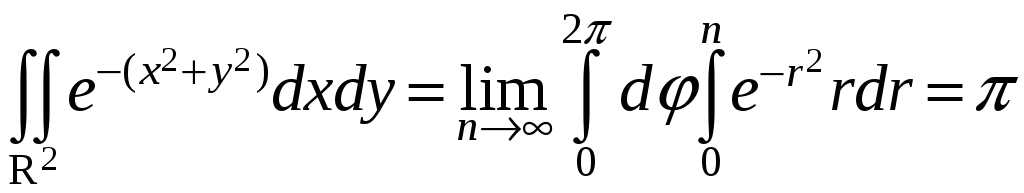б) .

Из равенства левых частей полученных соотношений а) и б) имеем значение интеграла Эйлера-Пуассона:

.
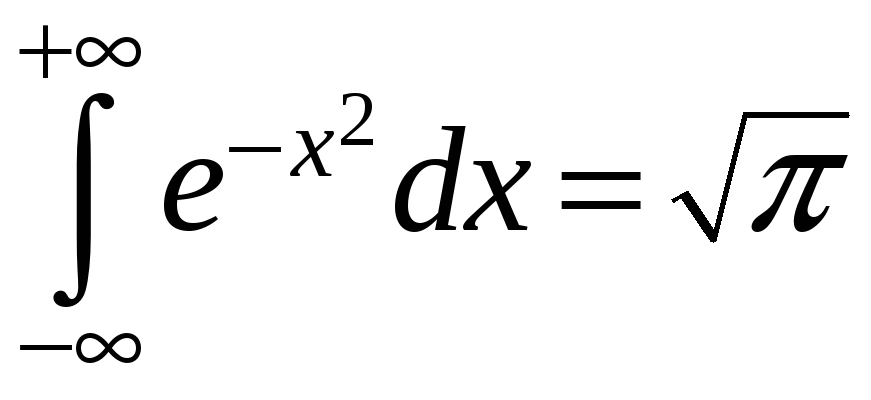