Лекция 8

Прямая и обратная задачи над вертикально намагниченным шаром.

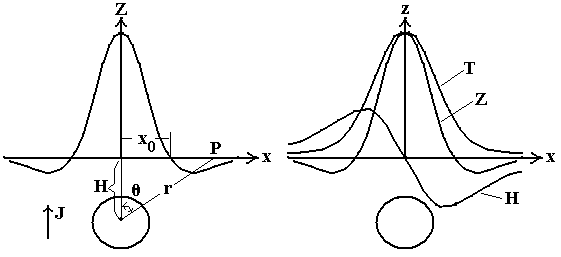
1. Прямая задача. Пусть вертикально намагниченный шар с центром на глубине залегает под началом координат (рис. 2). Необходимо определить напряженность поля вдоль профиля х. Потенциал шара можно представить как потенциал диполя, помещенного в его центре. Поэтому, потенциал шара с магнитным моментом M = Jv (или магнитной массой m = M), равен:

(1)

Отсюда, взяв производные, найдем элементы магнитного поля шара:

(2)

(3)

(4)

Анализ этих формул и построенных по ним графиков показывает, что над центром шара (х = 0) будут Z_max = T_max = 2Jv/μH³, а Н_а = 0. При х → ∞ аномалии исчезают. При х = ±1,41Н Z_a = 0, при x < 1,41H Z_a >0, а при x > 1,41H Z_a <0.

Таким образом, в плане над шаром изолинии Z_a и T_a будут иметь вид концентрических окружностей. При этом изолинии Z_a будут двух знаков, а T_a - одного.

2. Обратная задача. Решение уравнений (2 - 4) дает возможность по характерным точкам на графиках определить глубину залегания центра шара Н.

Характерными точками для шара являются:

1. Абцисса (значение х) для минимального значения Z_a (х_Zmin);

2. Значение х для Z_a = 0 (x_Z0);

3. Значение х для Z_a = 0.5Z_max (x_Z1/2);

4. Значение х для T_a = 0.5T_max (x_T1/2);

H = 0.7| x_Z0 | = 0.5| х_Zmin | = 1.8 | x_Z1/2 | = 1.5 | x_T1/2 |.

Знак абсолютной величины берется из-за того, что все графики над сферой симметричны относительно их экстремумов.

Зная Н можно вычислить магнитный момент шара: М = Jv = Z_maxμH^3/2 = T_maxμH^3/2 , а отсюда и радиус сферы.

Прямая и обратная задачи над намагниченным вертикальным бесконечно длинным столбом (стержнем).

Прямая задача. Пусть на глубине h залегает вершина бесконечно длинного столба (вертикального цилиндра или стержня) сечением s.

Его можно представить как тело одного полюса (m) с намагниченностью (J), направленной вдоль оси z, и "магнитной массой" m = Js. Так как нижний полюс столба расположен очень далеко, то его влиянием можно пренебречь и считать, что вся "магнитная масса" сосредоточена на вершине столба.

Необходимо найти напряженность поля вдоль профиля x над телом. Потенциал от верхнего полюса столба в точке P будет равен потенциалу точечной массы:

(5)

Составляющие поля выражаются производными потенциала по соответ­ству­ющим осям координат:

(6)

(7)

(8)

Используя полученные формулы, можно построить графики напряженности поля. Легко видеть, что над столбом будут максимумы T_a и Z_a, а значения их будут одного знака, положительные при вертикальной J. Горизонтальная составляющая (H) слева будет иметь максимум, а справа - минимум. Вдалеке от столба аномалии исчезают. В плане над таким столбом изолинии T_a и Z_a будут иметь вид концентрических окружностей одного знака.

Обратная задача. Решение уравнений (6 - 8) дает возможность по характерным точкам на графиках определить глубину залегания верхней кромки вертикального бесконечно длинного столба (h). Так центр столба находится в точке, где x = 0, Z_max = T_max = Js/μmh².

Для характерной точки получаем: h = 1,3| x_Z1/2 | = 1.3 | x_T1/2 |. Зная h можно оценить величину магнитной массы: m = Z_maxμh² = T_maxμh² = Js.

Так как J = æH, где æ - магнитная восприимчивость столба, то можно определить площадь поперечного сечения столба s.

Прямая и обратная задачи над вертикально намагниченным тонким пластом бесконечного простирания и глубины.

Пусть на глубине h параллельно оси y расположен бесконечно длинный вертикальный пласт (с толщиной l, меньшей глубины залегания), намагни­ченный вертикально.

Определим для простоты лишь Z_a вдоль оси x. Поскольку нижняя часть пласта расположена глубоко, то влияние магнитного полюса глубоких частей пласта будет мало, и можно считать, что магнитные массы сосредоточены вдоль поверхности в виде линейных полюсов. Магнитная масса единицы длины пласта равна dm/dy = Jl.

Разобьем пласт на множество тонких "столбов". Тогда притяжение пласта будет складываться из притяжения всех элементарных столбов, а вертикальная составляющая его магнитного притяжения будет равна интегралу в пределах от -∞ до +∞ (по оси y) выражения для притяжения элементарного столба. Потенциал элементарного тонкого столба равен

(9)

, а вертикальная составляющая dZ_a

(10)

откуда (11)

График Z_a будет иметь максимум над центром пласта и асимптотически стремиться к нулю при удалении от пласта. В плане над пластом будут вытянутые аномалии Z_a одного знака. Анализируя формулы (9 - 11), можно найти связи между глубиной залегания пласта (h) и x_1/2, т.е. абсциссой графика: h = x_1/2.

Магнитная масса единицы длины равна m = Jl = Z_maxμh/2, J = æH, отсюда можно рассчитать ширину пласта.

Прямая и обратная задачи для вертикально намагниченного горизонтального цилиндра бесконечного простирания.

Пусть на глубине H параллельно оси y расположен бесконечно длинный цилиндр с магнитным моментом единицы длины, равным M = Js, где J - интенсивность намагничивания, постоянная для всего цилиндра и направленная вертикально, s - поперечное сечение цилиндра.

Требуется определить напряженность поля вдоль оси . Поле такого цилиндра можно считать эквивалентным полю бес­конечного числа вертикальных магнит­ных диполей, центры которых располо­же­ны по оси цилиндра. Потенциал в точке P от элементарного диполя определяется согласно уравнению:

(12)

где . Потенциал всего цилиндра равен потенциалу от системы диполей, расположенных вдоль оси бесконечного цилиндра, или интегралу по объему цилиндра от выражения для потенциала элементарного диполя.

(13)

Легко видеть, что при х = 0 будет максимум Z_a, а при х = Н Z_a = 0. При  х  > 0 значения Z_a будут отрицательны, а при  х  < H – положительны. В плане над горизонтальным цилиндром будут вытянутые аномалии двух знаков.

При решении обратной задачи глубину залегания цилиндра можно определить по формулам: H = | x₀ | = 0.7| х_min |, где x₀ и х_min абциссы точек, в которых Z_a = 0 и Z_a = Z_max. Зная Н можно нацти погонную магнитную массу цилиндра M = Z_maxH²/2, откуда рассчитывается площадь сечения цилиндра.