Теоретические основы автоматизированного управления.-2

181

Для лучшей идентификации различных экземпляров документов рекомендуется оформлять их на бумаге различного цвета, например, белый — экземпляр поставщика, розовый — экземпляр отдела снабжения и т.д.

Проверка качества, количества и размещения товара. Важное значе-

ние в реализации плана закупок имеют приемка продукции, документальное оформление поставок, проверка качества и количества товаров. В первую очередь, необходимо удостовериться, что получен товар:

•нужного качества;

•в нужном количестве;

•от своего поставщика;

•в обусловленное время;

•за оговоренную цену.

Оформление поставок сопровождается следующими документами:

•копией бланка заказа;

•уведомлением об отгрузке;

•сопроводительным письмом;

•документом доставщика, в котором указываются название и адрес отправителя, описание продукции, количество мест, масса (вес) продукции, особенности транспортировки, название доставщика;

•подтверждением получения поставки;

•записью в книге регистрации товаров.

Качество поставляемых товаров должно удовлетворять предъявляемым требованиям. Отсутствие контроля качества закупок может привести:

•к дополнительным расходам, связанным с возвратом бракованных и недоброкачественных товаров;

•к остановке производства в случае, когда, например, вся партия продукции оказалась недоброкачественной и подлежит возврату;

•к судебным искам;

•к потере доверия потребителей своей продукции из-за поставок недоброкачественных материалов (деталей, изделий).

При проверке качества используются как сплошные, так и выборочные методы контроля. Использование выборочных методов контроля связано с определением «необходимого и достаточного размера выборки».

В целях экономии времени, усилий и соответственно денег следует поза-

ботиться о том, чтобы складские помещения, места разгрузки, приемки товара

были расположены как можно ближе друг к другу и недалеко от производственных помещений. Во избежание скопления транспорта на территории предприятия или у ворот склада, для экономии затрат труда на погрузочноразгрузочных работах составьте график поставок, согласованный со всеми поставщиками. Предусмотрите при этом, чтобы основное сырье поставлялось в строго определенные дни, а другие виды материалов — по мере необходимости. Такие меры позволят, кроме того, не отрывать рабочих основного производства для разгрузки неожиданно прибывшего транспорта.

182

5.4.5. Организация функционирования систем снабжения

Организация поставок материалов потребителю также может быть организована в виде прямых поставок через торговых агентов фирмы или поставок материалов через посредническую фирму.

Очевидно, что первый способ наиболее выгоден для предприятия. Вместе с тем в условиях плохо изученного рынка сырья, высокой диверсификации производства, освоения принципиально новой продукции предприятию бывает выгодно действовать через фирму-посредника, профессионально работающую на рынке. При этом услуги могут быть оказаны на уровне:

•профессионального подбора поставщика;

•исполнения организационной и финансовой частей сделок;

•комплексной поставки материалов потребителю.

Традиционная схема поставок основана на принципах хранения запасов в системе взаимодействующих складов поставщиков, потребителей, посредников, продавцов. Главный недостаток данного вида организации снабжения — большие накладные расходы (издержки), основными составляющими которых являются:

•затраты на обслуживающий персонал;

•затраты на транспортные средства;

•убытки от хранения запасов.

К этому же виду расходов можно отнести и капитальные вложения фирмы на строительство складских помещений, приобретение складского и транспортного оборудования.

Другой важной проблемой организации логистического звена «снабже-

ние» является резкое сокращение времени от возникновения рыночной по-

требности в материалах до их реальной поставки на производство.

Данная проблема требует разработки принципиально новых подходов к организации материально-технического обеспечения производства, основными из которых являются зародившиеся в недрах развития японской промышленности системы «Kanban» и «Точно в срок». Основная идея системы «Kanban» состоит в минимизации издержек на производственные запасы конечной продукции и комплектующих изделий, что достигается:

•производством и поставкой продукции в сроки, оговоренные с потребителем;

•изготовлением комплектующих не впрок, а непосредственно для подачи на сборочные операции;

•поставкой исходного сырья именно в тот срок, когда оно необходимо для изготовления изделий.

При системе «Kanban» план производства комплектующих изделий на данной технологической операции (участке) определяется, в основном, потребностями в этих комплектующих на последующей операции (участке), при этом

183

начало всему определяет конечный выпуск, под который подстраиваются все предшествующие этапы производства. Очевидно, что такая технология может быть использована при относительно стабильной производственной программе, а также незначительных отклонениях показателей загрузки оборудования от имеющихся мощностей. Вместе с тем номенклатура и объемы выпуска в рамках общей производственной программы могут изменяться.

Для внедрения этой системы необходимо наличие множества взаимозаменяемого оборудования, позволяющего выпускать разнообразные комплектующие, что, естественно, накладывает менее жесткие требования к наличию страховых запасов. Так, на многих японских фирмах, использующих эту технологию, запасы пополняются трижды в день. Устранение буферных складских запасов и усиление попарных связей между производственными участкамисмежниками увеличивает стабильность производственного процесса.

Вместе с тем отсутствие запасов требует:

•высокой надежности работы оборудования;

•высокого качества комплектующих изделий;

•наличия гибкого программируемого оборудования, способного быстро реагировать на изменение спроса.

Система не работоспособна при значительных колебаниях объема производственной программы предприятия.

Отличительными особенностями системы «Точно в срок» являются:

•поставка сырья и комплектующих изделий небольшими партиями, непосредственно на технологические операции, минуя складские помещения;

•отгрузка конечной продукции потребителям непосредственно с последней (сборочной) операции.

Для практической реализации этих принципов предприятие ориентируется на сокращение запасов и расстояний, что достигается за счет сокращения числа изделий в партии запуска и уменьшения страховых запасов. Производство мелкими партиями с большой частотой более соответствует высоким темпам потребления продукции, при этом сокращаются запасы, уменьшаются текущие издержки, быстрее выявляются причины и факторы выпуска продукции низкого качества. Аналогичные результаты достигаются и при сокращении страховых запасов.

Контрольные вопросы

1. Дайте определение логистической системы, поясните ее основное отличие от традиционных систем диспетчерского управления.

184

2.Представьте модели описания материального, информационного и финансового потоков в виде совокупности соответствующих логистических функций.

3.Дайте понятие логистической операции, покажите ее основное отличие от логистической функции.

4.Что такое логистические звенья и цепи? Поясните на примере задачу выбора оптимальной логистической цепи.

5.Перечислите базисные, ключевые и поддерживающие логистические функции, поясните логические связи между ними.

6.Дайте определение и основные характеристики микрологистической системы.

7.Объясните принципиальные схемы толкающей и тянущей систем управления материальными потоками.

8.Дайте определение и основные характеристики макрологистической системы.

9.Перечислите и охарактеризуйте основные функции и задачи закупочной логистики.

10.Опишите технологию выбора поставщика.

11.Перечислите основные методы определения потребности в материальных ресурсах.

12.Приведите технологию планирования и организации закупок.

13.Дайте сравнительные характеристики логистических систем «Kanban» и «Точно в срок».

185

6.МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОЦЕНКИ И АНАЛИЗА ПРОБЛЕМНЫХ СИТУАЦИЙ

6.1. Общая постановка задачи

В предыдущих разделах учебника проблемная ситуация рассматривалась как несоответствие между желаемым и фактическим состоянием системы. Относительно систем производственного назначения это может быть несоответствие между величинами планового и фактического объема продаж, финансовых ресурсов, уровнями рентабельности и т.д. При этом перед исследователем стоит следующая задача — измерить и сравнить желаемое и фактическое состоя-

ние системы по схемам:

<план — факт — норматив> →< Pt , Ft , Nt >;

<план — прогноз — норматив> →< Pt +k ,Qt +k , Nt +k >,

т.е. измерить и оценить величину проблемной ситуации в текущем и прогнозном интервалах времени. Количественная оценка рассогласования может быть представлена в виде соотношения разностей следующих величин:

При этом задача состоит в определении как индивидуальных характеристик проблемной ситуации относительно каждого показателя, описывающего проблему, так и некоторой интегральной характеристики проблемы в целом.

Основным понятием при комплексном оценивании проблемной ситуации является так называемое «таксономическое расстояние» [32]. Это расстояние между точками многомерного пространства ρ(xi , x j ) (двумя объектами сравне-

ния), исчисляемое чаще всего по правилам аналитической геометрии. Размерность пространства определяется числом показателей, по которым сравниваются объекты анализа. Исчисленные расстояния позволяют определить положение каждого объекта относительно остальных объектов и, следовательно, определить место этого объекта во всей совокупности, что делает возможным их упорядочение и классификацию.

В качестве наиболее употребляемой методики определения расстояния между двумя объектами используется обычное либо взвешенное Евклидово расстояние:

где αs — неотрицательный коэффициент, определяющий вес (значимость)

s-го показателя и принимающий значение от нуля до единицы;

xis , x js — значения s-го показателя для i-го и j-го объектов сравнения.

В случае, если объекты описываются дихотомическими признаками, используется уравнение Хеминга:

186

Как следует из выражения (6.3), расстояние между двумя объектами, описываемыми в двоичном пространстве, равно количеству несовпадений значений соответствующих признаков в рассматриваемой паре (xi, xj). В данном случае речь будет идти о вычислении расстояния между фактическими (прогнозными) и нормативными (плановыми) значениями показателей, описывающих проблемную ситуацию в рассматриваемой производственной системе:

где xit — фактическое значение i-го показателя, характеризующего проблемную

ситуацию в интервале t;

xit — его плановое (нормативное) значение.

C учетом вышеизложенного измерение и анализ проблемной ситуации состоит в периодическом сравнении желаемого и фактического состояния системы в настоящем, нормативного и прогнозируемого — в будущем и в сопос-

тавлении отклонений с некоторой пороговой величиной: Zt ≤ ∆Zt . Очевидно,

что если в интервале t эти условия не выполняются, то проблемная ситуация либо наступила, либо наступит в будущем, и требуется вмешательство лиц, принимающих решение. Практическая реализация задачи предсказания проблемной ситуации требует наличия множества математических моделей исследуемых систем, позволяющих реализовать функцию прогнозирования.

При построении таких моделей инертность развития производственных систем следует понимать двояко: как сохранение в основных чертах взаимосвязей прогнозируемых параметров с другими параметрами и как сохранение общей тенденции изменения параметров во времени.

Наличие инертности первого вида позволяет представлять поведение изучаемого объекта в виде аналитического выражения, которое связывает изменение некоторого показателя эффективности системы с изменением ряда

Зависимости такого типа получили название уравнений регрессии, либо моделей производственных функций. Инертность второго вида позволяет подобрать аналитическую зависимость изменения наблюдаемого явления во времени, т.е. определяется выражение типа

можно говорить о некоторой обобщенной модели, когда к факторамаргументам добавляется величина зависимой переменной в прошедшем периоде времени, т.е. в прогнозе используется выражение типа

187

Во всех случаях реализация функции прогнозирования осуществляется путем подстановки в аналитические выражения с численно оцененными параметрами значений независимых переменных. При этом различают точечный и интервальный прогноз. В последнем случае значение прогнозируемого показателя задается в области доверительного интервала.

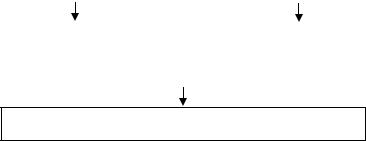
Исходя из вышеизложенного, укрупненная схема определения и оценивания проблемной ситуации может быть представлена следующей схемой (рис. 6.1):

Определение и оценивание проблемы

Рис. 6.1. Укрупненная схема определения проблемной ситуации

Нормативный (целевой) прогноз основан на директивном задании факто- ров-аргументов в используемой модели прогноза. В свою очередь, при инерционном прогнозировании допускается, что изменение значений факторов-аргу- ментов будет происходить в связи со сложившимися в прошлом закономерностями, и для определения этих тенденций также требуется прогнозирование.

6.2. Построение многофакторных регрессионных моделей

6.2.1. Этапы построения регрессионных моделей

При построении регрессионных зависимостей [8] в настоящее время различают структурный и функциональный подходы. Структурный подход основывается на структурном анализе производственной системы, путем декомпозиции ее до некоторых «элементарных» составляющих, характеризующихся вполне конкретными технологическими параметрами, и описании этих элементов с помощью аналитических выражений, отражающих физические процессы и явления. Надо сказать, что этот способ создания моделей позволяет определять зависимости, наиболее адекватные реальным процессам. Вместе с тем он достаточно трудоемок и требует разработки некоторых неформальных методов декомпозиции и идентификации.

Более распространен в настоящее время функциональный подход, основывающийся на представлении производственной системы в виде модели «черного ящика». В этом случае делается предположение о сохранении

188

в математической модели объекта тенденций, которые наблюдались в прошлом, и для ее нахождения может быть использован известный метод наименьших квадратов.

Если производственная система является сложным многоцелевым объектом, то следует использовать разумную комбинацию структурного и функционального подходов. В этом случае на первом этапе производственную систему разбивают на «элементарные» и одно-продуктовые объекты, а затем для каждого объекта находят свои математические выражения. Обобщенная схема определения регрессионных моделей с использованием функционального подхода представлена на рис. 6.2. Кратко остановимся на описании каждого из этапов.

Выбор и обоснование факторов-аргументов

Выбор и обоснование формы уравнения регрессии

Определение параметров уравнения регрессии

Статистическое оценивание параметров уравнения регрессии

Оценка точности и надежности модели

Рис. 6.2. Основные этапы построения регрессионной модели

6.2.2. Выбор и обоснование факторов-аргументов

Познавательная ценность уравнения регрессии повышается, если в него включается наибольшее количество факторов, влияющих на рассматриваемый результативный признак. Естественно, возникают вопросы: сколько и каких факторов следует включать в уравнение регрессии, когда включение дополнительных факторов себя оправдывает и в каком случае это нецелесообразно.

Поставленный вопрос должен решаться с одновременным применением как экономико-качественных, так и математико-статистических критериев.

При построении многофакторного уравнения регрессии в первую очередь должен быть проведен анализ качественной стороны изучаемых взаимосвязей, поэтому до построения общей регрессионной или корреляционной модели необходимо иметь определенную научную теорию, в соответствии с которой будут интерпретироваться полученные результаты, т.е. рассматривать в составе модели факторы, имеющие причинно-следственные связи с результатом.

189

После выдвижения определенной гипотезы о качественной стороне взаимосвязей при помощи методов корреляционного анализа можно, во-первых, проверить по определенному фактическому материалу правильность выдвинутой теории для ее подтверждения или отклонения, во-вторых, изучить количественно комплексную взаимосвязь факторов и явлений.

Практически, на основе качественного анализа составляется перечень достаточно большого количества факторов, которые могут быть причинами изучаемого результативного признака. Отбор факторов целесообразно проводить в две стадии. На первой стадии (стадия качественного анализа) отбираются факторы, качественно связанные с исследуемой проблемой, численные значения (данные) которых можно собрать или определить. Затем, на второй стадии в процессе количественного анализа отбираются факторы, влияние которых на результативный показатель существенно. Чтобы облегчить отбор существенных факторов на второй стадии анализа, рекомендуется уже на первой стадии отобрать только те из них, которые при логическом анализе окажутся наиболее важными. От менее значимых факторов следует отказаться в самом начале исследования.

Так, например, на первом этапе в модель можно включать только те факторы, коэффициент корреляции которых с результирующим показателем не менее 0,3. Перечень отобранных на первой стадии факторов не должен быть слишком обширным. Кроме того, отобранные факторы не должны иметь тесных корреляционных связей между собой. Качественные факторы выражать через количественные и включать их в модель не рекомендуется. Если же один или несколько качественных признаков в пределах предпринятого исследования так важны, что отказаться от них невозможно, следует всю совокупность наблюдений классифицировать в соответствии с выделяемым значением атрибутивного признака и количественный анализ провести в каждой выделенной группе в отдельности.

6.2.3. Выбор и обоснование формы уравнения регрессии

Выбор формы, или класса уравнения, по которому будут проведены расчеты, равносилен выдвижению в общем виде некоторой гипотезы о форме связей между выбранными факторами и результирующим признаком.

Выбор той или иной формы связей определяется следующими соображениями:

•избранный тип уравнения регрессии должен отражать качественный характер экономических закономерностей, присущих изучаемым явлениям;

•для оценивания параметров методом наименьших квадратов необходимо использовать уравнения, которые по отношению к определяемым константам регрессии являются линейными или могут быть к таким приведены путем несложных преобразований;