Прикладные математические методы в радиотехнике.-1

31

Заметим, что полученное начальное условие, совпало с ранее найденным значением переходной характеристики, при t 0 .

Приступаем к интегрированию дифференциального уравнения с целью определения отклика дифференцирующей RC - цепи на единичный скачок на входе.

2.2. Метод Лагранжа или метод вариации произвольных постоянных. Согласно методу Лагранжа, решение неоднородного дифференциального уравнения, записывается аналогично решению однородного уравнения, только константа при фундаментальном решении заменяется неизвестной функцией времени

v(t) C(t) e t .

Подстановка предполагаемого решения в исходное уравнение дает

C'(t) e t C(t) e t C(t) e t (0) ,

откуда

C'(t) e t (0)

или

C'(t) (0) e t .

Для определения варьируемой постоянной C(t) проинтегрируем последнее выражение

C(t) (0) e tdt 1 C ,

где C - новая постоянная интегрирования. Здесь при интегрировании учтено селектирующее свойство - функции

f (t) (0) dt f (0) .

Постоянную интегрирования определим из начальных условий. Для этого подставим выражение C(t) в общее решение

v(t) (1 C) e t e t C e t .

Из начального условия v(0) 1 , при t 0 , следует, что

1 1 C ,

откуда получаем

C 0 .

Таким образом, частное решение дифференциального уравнения, соответствующее переходной характеристике дифференцирующей RC - цепи, получаем в виде

v(t) e t h(t) .

Заметим, что полученное выражение совпадает с решением, полученным операторным методом.

2.3. Метод Коши – интегрирования дифференциальных уравнений. Метод Коши позволяет, используя начальные условия, сразу записать частное решение дифференциального уравнения. Согласно методу Коши, решение отдельного либо системы дифференциальных уравнений первого порядка

32

y'(t) A y(t) F(t) ,

где y(t), y'(t), F(t) - в общем случае векторы функций; A - матрица коэффициентов, может быть представлено в виде

t

y(t) e A t y(0) e A (t ) F ( ) d ,

0

где - параметр времени; eA t - в случае системы уравнений, экспонента от матрицы коэффициентов.

Применительно к нашему дифференциальному уравнению, решение запишется в виде

t

v(t) e t v(0) e (t ) (0) d .

0

Принимая во внимание, что v(0) 1 , и, интегрируя второе слагаемое,

получаем решение, соответствующее переходной характеристике дифференцирующей RC - цепи, в виде

Учитывая, что первое слагаемое определено при t 0 , а второе слагаемое при t 0 , после их объединения, окончательно получаем

v(t) e t h(t) .

Как видим, полученное решение совпадает с предыдущими решениями и представляет переходную характеристику дифференцирующей RC - цепи, где в качестве реакции на единичный скачок на входе, рассматривается напряжение на выходе.

3. Импульсная характеристика. Перейдем к определению импульсной характеристики. В качестве входного воздействия, в данном случае используется единичный импульс

E( p) 1 (0) e(t) .

3.1. Операторный метод. При воздействии на вход единичного импульса изображение выходного напряжения запишется в виде

V ( p) p . p

Отметим, что в данном случае дробно-рациональное выражение для изображения выходного напряжения имеет одинаковые степени числителя и знаменателя. Для перехода в область оригиналов необходимо, чтобы степень знаменателя была выше степени числителя, в связи с чем, разобьем дробно-рациональное выражение на элементарные дроби, поделив числитель на знаменатель

33

Используя таблицы обратного преобразования Лапласа, устанавливаем соответствие между изображениями и оригиналами

На основании установленных соответствий, находим оригинал выходного напряжения, соответствующий импульсной характеристике дифференцирующей RC - цепи

значение импульсной характеристики, при t , равно нулю g( ) 0 .

Как видим, в соответствии с теоремами операционного исчисления о начальном и конечном значении функции, выполняются соотношения вида

Отметим, что импульсная характеристика может быть получена из переходной характеристики на основании теоремы операционного исчисления о дифференцировании оригинала

v'(t) p V ( p) v( 0) .

Данное интегральное соотношение может быть переписано в виде p V ( p) v'(t) v( 0) (0) .

Так как реакция на выходе в области изображений теперь соответствует p V ( p) , то последнее соотношение можем переписать в

виде

g(t) h'(t) (0) h(0) .

Используя полученное выражение, и, учитывая, что h(0) 1, вновь

получаем выражение для импульсной характеристики, дифференцируя переходную характеристику

g(t) h'(t) (0) h(0) (e t )' (0) 1 (0) e t .

Поскольку начальное значение ненулевое, импульсная характеристика содержит - функцию.

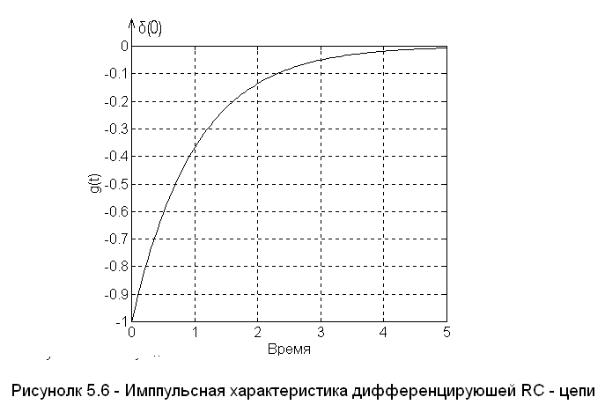
Вид импульсной характеристики дифференцирующей RC - цепи, при1, приведен на рисунке 5.6.

34

Формирование и интегрирование дифференциального уравнения.

Дифференциальное уравнение цепи относительно выходного напряжения, как и в предыдущем случае, формируем на основе операторного выражения для выходного напряжения, путем замены оператора Лапласа p оператором дифференцирования d / dt .

Используя операторное выражение для изображения выходного напряжения и, учитывая, что в данном случае E( p) 1, получаем

Перегруппировывая полученное выражение, приходим к записи дифференциального уравнения дифференцирующей RC - цепи

v'(t) v(t) '(0) .

Полученное уравнение является неоднородным обыкновенным дифференциальным уравнением первого порядка, содержащим в правой части - функцию. В нормальной форме Коши, уравнение, разрешенное относительно старшей производной, имеет вид

v'(t) v(t) '(0) .

При интегрировании полученного неоднородного обыкновенного дифференциального уравнения, с целью получения частного решения, нам понадобятся начальные условия.

Определение начальных условий. Для определения начальных условий воспользуемся модифицированной теоремой операционного исчисления о начальном значении функции

35

Отметим, что в полученном дробно-рациональном отношении степень числителя выше степени знаменателя и простое взятие предела дает сразу , скрывая конечные составляющие начального значения.

В данной ситуации целесообразно воспользоваться модификацией теоремы операционного исчисления о начальном значении функции.

Модификация теоремы о начальном значении заключается в том,

что вначале путем последовательного деления числителя на знаменатель выделяем целую и дробную части. Составляющие целой части дадут - функцию и ее производные, а остаток от деления в пределе, при p

даст конечную часть начального условия.

Следуя указанной модификации теоремы о начальном значении, получаем

Заметим, что полученное начальное условие, совпало с ранее найденным значением импульсной характеристики, при t 0 .

Приступаем к интегрированию дифференциального уравнения с целью определения отклика дифференцирующей RC - цепи на единичный импульс на входе.

3.2. Метод Лагранжа или метод вариации произвольных постоянных. Согласно методу Лагранжа, решение неоднородного дифференциального уравнения, записывается по аналогии с решением однородного уравнения, только константа при фундаментальном решении заменяется неизвестной функцией времени

v(t) C(t) e t .

Подстановка предполагаемого решения в исходное уравнение дает

C'(t) e t C(t) e t C(t) e t '(0) ,

или

C'(t) '(0) e t .

Для определения варьируемой постоянной C(t) проинтегрируем полученное выражение

C(t) '(0) e tdt C ,

где C - новая постоянная интегрирования. Здесь при интегрировании учтено селектирующее свойство производной от - функции

f (t) '(0) dt f '(0) .

Постоянную интегрирования определим из начальных условий. Для этого подставим выражение C(t) в общее решение

v(t) ( C) e t e t C e t .

36

Из начального условия v(0) (0) , при t 0 , следует, что

(0) C ,

откуда получаем

C(0) .

Врезультате, частное решение дифференциального уравнения, соответствующее импульсной характеристике интегрирующей RC - цепи, получаем в виде

v(t) ( (0) ) e t (0) e t g(t) .

Заметим, что полученное выражение совпадает с решением, полученным операторным методом.

3.3. Метод Коши – интегрирования дифференциальных уравнений. Метод Коши позволяет, используя начальные условия, непосредственно записать частное решение дифференциального уравнения. Согласно методу Коши, решение отдельного либо системы дифференциальных уравнений первого порядка

y'(t) A y(t) F(t) ,

где y(t), y'(t), F(t) - в общем случае векторы функций; A - матрица коэффициентов, может быть представлено в виде

t

y(t) e A t y(0) e A (t ) F ( ) d ,

0

где - параметр времени; eA t - в случае системы уравнений, экспонента от матрицы коэффициентов.

Применительно к нашему дифференциальному уравнению, решение запишется в виде

слагаемые при t 0 , после их объединения, окончательно получаем v(t) (0) e t g(t) .

Как видим, полученное решение совпадает с предыдущими решениями и представляет импульсную характеристику дифференцирующей RC - цепи, где в качестве реакции на единичный импульс на входе, рассматривается напряжение на выходе.

37

Таким образом, все три метода, предлагаемой методики исследования временных характеристик (операторный, Лагранжа и Коши), дают совпадающие результаты при их корректном применении.

Применение конкретного метода, определяется, как правило, субъективными и объективными факторами. Так операторный метод подкупает своей простотой, но проблематичен при автоматизации численно-аналитических исследований. Метод Коши, напротив, наиболее формализован и прост для реализации в современных системах аналитического исследования. Метод Лагранжа занимает в этом отношении промежуточное положение. Овладение каждым из проиллюстрированных методов позволит приобрести навык математических исследований, который пригодится при освоении специальных дисциплин и последующей инженерной и исследовательской деятельности.

Рассмотренные нами примеры определения временных характеристик простых RC - цепей, призваны проиллюстрировать основные понятия и определения, предлагаемую методику исследования, а также подчеркнуть актуальность математического обоснования элементов методики исследования.

6 ЗАКЛЮЧЕНИЕ

Таким образом, в методическом пособии сформулировано задание на контрольную работу, даны краткие методические указания, представлено краткое содержание теоретической части и приведены примеры исследования характеристик простейших аналоговых цепей.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1.Иванов В.А., Чемоданов Б.К., Медведев В.С. Математические основы теории автоматического регулирования. / Под ред. Б.К. Чемоданова. -

М.: Высшая школа, 1971.- 808 с., 1974.- 754 с.

2.Иванов В.А., Чемоданов Б.К., Медведев В.С., Ющенко А.С. Математические основы теории автоматического регулирования. / Под ред. Б.К. Чемоданова, Изд. 2-е, доп., в 2-х томах – Т. 1. - М.: Высшая школа, 1977.- 366 с.; Т. 2. - М.: Высшая школа, 1977.- 455 с.

3.Овчиннников П.Ф., Лисицын Б.М., Михайленко В.М. Высшая математика: Учебное пособие. – К.: Выща школа, 1989.- 679 с.

4.Пономарев К.К. Специальный курс высшей математики (дифференциальные уравнения, краевые задачи, интегральные уравнения). – М.: Высшая школа, 1974.- 367 с.

5.Пантелеев А.В., Якимова А.С., Босов А.В. Обыкновенные дифференциальные уравнения в примерах и задачах: Учебное пособие.

– М.: Высшая школа, 2001.- 376 с.

38

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ ПО ДИСЦИПЛИНЕ ПММР

Предлагаемые вопросы призваны выработать представление об изучаемой дисциплине «Прикладные математические методы в радиотехнике» (ПММР), ориентировать студента на определенный уровень знаний полученных из предыдущих дисциплин (Высшая математика, Линейная алгебра, Теория цепей, Теория сигналов, Микроэлектроника), а также подготовить для творческого восприятия последующих дисциплин радиотехнического профиля.

1.Цель и содержание курса ПММР.

2.Задачи курса ПММР.

3.Понятия устройства, схемы, цепи, модели.

4.Компонентные и топологические уравнения.

5.Топологические матрицы.

6.Топологические законы цепей.

7.Компонентные уравнения цепей.

8.Особенности компонентных уравнений инерционных элементов.

9.Понятие графа, дерева графа, узла, сечения, контура.

10.Модели элементной базы.

11.Идеальный операционный усилитель и его модель.

12.Независимые источники, назначение и свойства.

13.Управляемые источники и их использование.

14.Модели сигнала в частотной и временной области.

15.Тестовые сигналы, используемые в радиотехнике.

16.Математическая модель цепи в частотной области.

17.Узловая система уравнений, свойства, методы формирования.

18.Линейность узловой системы уравнений.

19.Порядок узловой системы уравнений.

20.Содержание метода узловых потенциалов.

21.Понятие исходного состояния покоя.

22.Определение передаточной характеристики (функции).

23.Определение частотной характеристики (функции).

24.Связь передаточной и частотной характеристик.

25.Понятия ЧХ, АЧХ и ФЧХ.

26.Простейшие RC- и RL-цепи и их передаточные характеристики (функции).

27.Понятие постоянной времени.

28.Понятие фильтра - ФНЧ, ФВЧ, полосовой фильтр, заграждающий фильтр.

29.Понятие полосы пропускания, заграждения.

30.Понятие граничной частоты АЧХ цепи.

39

31.Связь постоянной времени с граничной частотой простых RC- и RLцепей.

32.Определение характеристического уравнения по передаточной функции.

33.Методы определения передаточных и частотных характеристик по схеме.

34.Понятие четырехполюсника, системы параметров, канонические схемы соединения.

35.Понятие многополюсника, системы параметров, переход от многополюсника к четырехполюснику.

36.Классические системы параметров и их связь.

37.Понятие линейной алгебраической системы уравнений.

38.Методы решения линейных алгебраических систем уравнений.

39.Понятие определителя, минора и алгебраического дополнения.

40.Однородные и неоднородные системы линейных алгебраических уравнений.

41.Признаки существования решения неоднородной линейной системы.

42.Особенности решения однородных линейных алгебраических систем уравнений.

43.Проблема собственных значений и векторов.

44.Понятия собственных значений и векторов.

45.Понятия характеристической матрицы и характеристического уравнения.

46.Методы определения собственных значений.

47.Связь собственных значений характеристической матрицы и корней характеристического уравнения.

48.Понятие модальной матрицы и методы ее представления.

49.Проблема кратности собственных значений и векторов.

50.Понятие аналитической функции от матрицы и способы ее представления.

51.Суть интегрального преобразования Лапласа.

52.Прямое и обратное преобразования Лапласа - основные понятия.

53.Основные теоремы преобразования Лапласа.

54.Основы операционного исчисления.

55.Условия существования преобразования Лапласа.

56.Понятие обобщенных функций.

57.Расширение операторного метода на обобщенные функции.

58.Функция Хевисайда и дельта-функция.

59.Способы выполнения обратного преобразования Лапласа.

60.Теорема о дифференцировании оригинала.

61.Теоремы о начальном и конечном значениях.

40

62.Понятие переходной функции цепи.

63.Понятие импульсной функции цепи.

64.Связь переходной и импульсной функций.

65.Связь передаточной и импульсной функций.

66.Простейшие RC- и RL-цепи и их переходные характеристики (функции).

67.Понятие времени нарастания переходной характеристики.

68.Связь времени нарастания и постоянной времени простых RC- и RLцепей.

69.Математическая модель цепи во временной области.

70.Способы аналитического определения временных характеристик цепи (системы).

71.Переход от передаточных функций к дифференциальным уравнениям.

72.Определение характеристического уравнения по дифференциальному уравнению.

73.Понятие дифференциального уравнения, типы дифференциальных. уравнений.

74.Обыкновенные дифференциальные уравнения.

75.Суть решения дифференциального уравнения.

76.Отличие обыкновенных дифференциальных уравнений от уравнений в частных производных.

77.Системы дифференциальных уравнений.

78.Порядок дифференциального уравнения.

79.Однородное и неоднородное дифференциальные уравнения.

80.Дифференциальные уравнения с постоянными и переменными коэффициентами.

81.Дифференциальные уравнения с периодическими коэффициентами.

82.Линейные и нелинейные дифференциальные уравнения.

83.Понятие общего решения дифференциальных уравнений.

84.Понятие частного решения дифференциальных уравнений.

85.Понятия независимых, начальных и граничных условий.

86.Содержание задачи Коши.

87.Содержание граничной или краевой задачи.

88.Понятие фундаментальной системы решений.

89.Условие независимости фундаментальной системы решений.

90.Общее решение однородных дифференциальных уравнений.

91.Общее решение неоднородных дифференциальных уравнений.

92.Переход от дифференциального уравнения высокого порядка к системе дифференциальных уравнений первого порядка.

93.Методы аналитического интегрирования дифференциальных уравнений.

94.Операторный метод решения дифференциальных уравнений.