
Информатика.-7
.pdf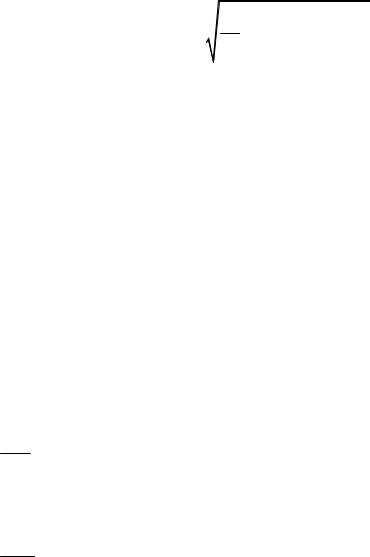
ностью. Поэтому не имеет смысла добиваться выполнения условия Лагранжа, чтобы интерполирующая функция обязательно проходила бы через узловые точки. Достаточно того, чтобы ошибки интерполяции (отклонения или остатки) были бы минимальны.
Предположим, что интерполирующая функция имеет вид
(x) c1 1(x) c2 2 (x) ... cm m (x),
где 1(x), 2 (x),..., m (x) – базисные функции, выбираемые исхо-
дя из предметной области исследования.
Погрешность интерполяции в точке x i равна | (xi ) yi |. Среднеквадратичная ошибка интерполяции в точках x1,
x2 ,..., xN
|
1 |
N |
|
(xi ) yi 2 . |
N i 1
Обозначим Q значение суммы:
N
Q (xi ) yi 2.
i 1
Задача интерполяции по методу наименьших квадратов сводится к нахождению значений коэффициентов c1, c2 , ..., cm , при
которых величина Q будет иметь минимальное значение.
Для нахождения значений c1, c2 , ..., cm требуется вычислить частные производные величины Q по этим коэффициентов, приравнять их к нулю и решить систему линейных уравнений:
Qc1
Q
c2
Qcm
n
0, 2 c1 1(xi ) c2 2 (xi ) ... cm m (xi ) yi 1(xi ) 0,
i 1
n
0, 2 c1 1(xi ) c2 2 (xi ) ... cm m (xi ) yi 2 (xi ) 0,
i 1
n
0 2 c1 1(xi ) c2 2 (xi ) ... cm m (xi ) yi m (xi ) 0.
i 1
– 101 –
Сократим на 2 левую часть уравнений, раскроем скобки и перенесем слагаемые, не зависящие от c1,c2 ,...,cm , в правую часть
уравнений. В результате получим систему линейных уравнений
|
n |
n |
c1 1(xi ) 1(xi ) ... cm m (xi ) 1(xi ) yi 1(xi ), |
||
i 1 |
i 1 |
|
|
n |
n |
|
|
(xi ) 2 (xi ) ... cm m (xi ) 2 (xi ) yi 2 (xi ) , |
c1 1 |
||
i 1 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
(xi ) m (xi ) ... cm m (xi ) m (xi ) yi m (xi ). |
c1 1 |
||
i 1 |
i 1 |
|
В матричной форме такая система имеет вид
( 1 1)
( 1 2 )
( 1 m )
( |
) |
( |
m |
) c |
|
|
( y) |
|
|||||||||||
1 2 |
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
||||
( 2 2 ) |
( 2 m ) c2 |
|
|
( 2 y) |
, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
( |
|
m |
) |
|
( |
m |
|
m |
) c |
|
( |
m |
y) |
|
|||||
2 |
|
|
|
|
|
|
m |
|
|
|
|
|
|||||||
n |
n |
где ( j k ) j (xi ) k (xi ) , ( j y) j (xi ) yi . |
|
i 1 |
i 1 |
Введем обозначения:
|
( ) |
( |
|
) |
( |
|
) |
|
||||||||
|
1 |
1 |
|
1 |
2 |
|
|
|
|
1 |
m |
|
|
|
||
|
( 1 2 ) |
( 2 2 ) |
( 2 m ) |
, |
||||||||||||
Γ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
( |
m |
) |
( |
|
m |
) |
|
( |
m |
|
m |
) |
|
|||
|
1 |
|
2 |
|
|
|
|
|
|
|
||||||
тогда получим матричное уравнение
Γ C Y ,
c |
|
|
( |
y) |
|
||
1 |
|
|
|
1 |
|
|
|
c2 |
|
|
( 2 y) |
, |
|||
C |
|
, Y |
|
|
|||
|
|
|
|
||||
c |
|
( |
m |
y) |
|
||
m |
|
|
|
|
|
||
где Γ – квадратная матрица, имеющая размер m m, называемая матрицей Грама.
Свойства матрицы Грама:
1)матрица Грама является квадратной;
2)она является симметричной.
–102 –
Вектор-столбец неизвестных коэффициентов c1,c2 ,...,cm определяется по формуле
C Γ 1 Y ,
где Γ 1 – квадратная матрица, обратная матрице Грама. Рассмотрим конкретный пример. Даны результаты измере-
ний: {0; 0}, {1; 0,5}, {2; 2}, {3;1,5}. Требуется по методу наи-
меньших квадратов провести прямую, проходящую через начало координат. Уравнение прямой, проходящей через начало коорди-
нат, имеет |
вид |
y kx . Тогда |
имеем: m 1, |
c1 k , |
1(x) x . |
|||
В данном случае |
|
|
|
|
|
|
||
|
|
n |
|
|
n |
|
|
|
|
|
( 1 1) 1(xi ) 1(xi ) xi2 , |
|
|
||||
|
|
i 1 |
|
|
i 1 |
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
( 1 y) 1(xi ) yi (xi yi ) . |
|
|
||||
|
|
i 1 |
|
|
i 1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
xi yi |
|
|
Значение c |
определяется по формуле c |
i 1 |
. Для при- |
|||||
n |
||||||||
|
1 |
|
|
|
1 |
|
||
|
|
|
|
|
|
xi2 |
|
|
веденных результатов измерений |
i 1 |
|
||||||
|
|
|||||||
4 |
|
|
|
|
4 |
|
|
|
xi2 |
0 1 4 9 14 ; |
xi yi 0 0,5 4 4,5 9 ; |
||||||
i 1 |
|
|
|
9 |
i 1 |
|
|
|
|
|
c |
0,625 . |
|
|
|||
|
|
|
|
|
||||
|
|
1 |
14 |
|
|
|
||
|
|
|
|
|
|
|||
Получаем уравнение прямой y 0,625x , проходящей через
начало координат. Задача решена.
Рассмотрим случай, когда результаты измерений {0; 0}, {1; 0,5}, {2; 2}, {3;1,5} требуется аппроксимировать произвольной прямой. В этом случае уравнение прямой имеет вид y kx b.
Тогда имеем: m 2, c1 k , 1(x) x , c2 b , 2 (x) 1.
– 103 –

|
n |
n |
|
В данном случае |
( 1 1) xi2 , |
( 1 2 ) xi , |
( 2 2 ) n , |
|
i 1 |
i 1 |
|
n |
n |
|
|
( 1 y) xi yi , ( 2 y) yi . Матрица Грама имеет вид
i 1
n xi2i 1
Γ ni 1 xi
|
|
i 1 |
|
|
|
|
n |
|
|
|
|
|
|
xi |
14 |
6 |
c |
|
|
|
i 1 |
|
, |
||||
|
|
|
, C 1 |
|
||
|
|
6 |
4 |
c |
|
|
n |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем решение методом Крамера:
n xi
i 1 Y
146 64 14 4 6 6 56 36 20;
|
|
9 |
6 |
|
9 4 4 6 36 24 12; |
|||||
|
|
|||||||||
1 |
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
14 |
9 |
|
14 4 6 9 56 54 2. |
||||
|
|
|||||||||
|
|
|
6 |
4 |
|
|
||||
yi 9 .4
Получаем значения: c1 12 : 20 0,6 ; c2 2 : 20 0,1.
Уравнение прямой имеет вид y 0,6x 0,1. Задача решена.
Рассмотрим более сложный случай, когда результаты измерений {0; 0}, {1; 0,5}, {2; 2}, {3;1,5} требуется аппроксимировать
параболой. В общем случае уравнение параболы принимает вид
y a |
a x a |
x2 . Тогда имеем: |
m 3, c |
a , |
(x) 1, c |
a , |
|||||
|
|
0 |
1 |
2 |
|
|
1 |
0 |
1 |
2 |
1 |
|
2 |
(x) x , c a , (x) x2 . |
|
|
|
|
|
||||
|
|
3 |
|
2 |
3 |
|
n |
|
n |
||
|
|
|
|
|
|
|
|
|
|||
|
|
В данном случае ( 1 1) n , |
( 2 2 ) xi2 |
, |
( 3 3 ) xi4 , |
||||||
|
|
|
|
|
|
|
|
i 1 |
|
i 1 |
|
|
|
|
n |
|
|
n |
|
n |
|
|
n |
( 1 2 ) xi , |
|
|
( 1 3 ) xi2 , |
( 2 3 ) xi3 |
, |
( 1 y) yi , |
|||||
|
|
|
i 1 |
|
|
i 1 |
|
i 1 |
|
i 1 |
|
|
|
|
n |
|
|
n |
|
|
|
|
|
( 2 y) xi yi , ( 3 y) xi2 yi . |
|
|
|
|
|
||||||
|
|
|
i 1 |
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
– 104 – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
Для данных |
точек |
имеем: |
n 4, |
xi 6 , |
xi2 |
14 , |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
i 1 |
|
4 |
4 |
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
xi3 36, |
xi4 98, yi 4 , xi yi |
9, xi2 yi |
22 . |
|
||||||||||||||||||||||||
i 1 |
i 1 |
|
i 1 |
|
i 1 |
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|||||||
Матрица Грама принимает вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
4 6 |
14 |
|
|
c |
|
|
|
|
4 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
C |
1 |
|
, Y |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Γ 6 14 |
36 , |
c2 |
|
|
9 . |
|
|
||||||||||||||||
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
14 |
98 |
|
|
c3 |
|
|
|
|
22 |
|
|
|
||||||||||
Найдем решение методом Крамера: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
4 |
6 |
14 |
|
|
80; |
|
|
|
|
4 |
|
|
6 |
14 |
|
12 ; |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
6 |
14 |
36 |
|
|
1 |
|
|
9 |
|
|
14 |
36 |
|
|
|||||||||||
|
|
|
|
14 |
36 |
98 |
|
|
|
|
|
|
|
22 |
|
36 |
98 |
|
|
|
|
|
|
|
||||
|
|
|
4 |
4 |
14 |
|
|
|
|
|
|
|
|
|
4 |
|
6 |
|
4 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
6 |
9 |
36 |
|
108; |
3 |
|
6 |
|
14 |
|
9 |
|
|
20 . |
|
||||||||||
|
|
|
14 |
22 |
98 |
|
|
|
|
|
14 |
36 |
|
22 |
|
|
|
|
|
|||||||||
Получаем: |
|
c1 12 :80 0,15 , |
|
|
|
c2 108 : 80 1,35, |
||||||||||||||||||||||
c3 20 :80 0,25.
Уравнение параболы имеет вид y 0,15 1,35x 0,25x2 .
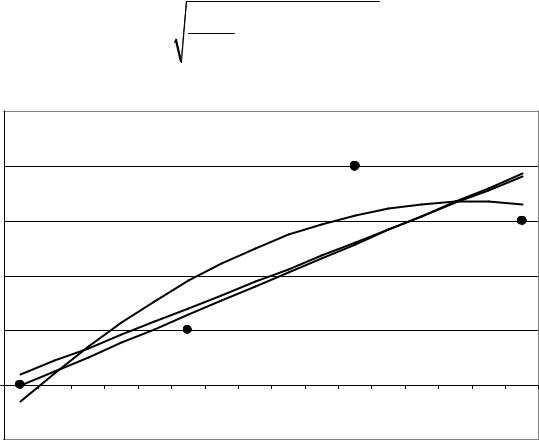
На рис. 5.4 показаны графики трех |
функций: y 0,625x , |
|
y 0,6x 0,1, |
y 0,15 1,35x 0,25x2 , |
полученных методом |
наименьших квадратов.
Значение величины Q , определяющей погрешность интерполяции, составило:
0,71 – при аппроксимации прямой, проходящей через начало координат;
0,7 – при аппроксимации произвольной прямой;
0,45 – при аппроксимации параболой.
Увеличение степени полинома приводит, с одной стороны, к уменьшению суммарной ошибки Q , с другой стороны – к уве-
личению времени вычисления неизвестных коэффициентов
– 105 –
c1,c2 ,...,cm . Для оценки приемлемого значения числа степени |
|||||||||||||||
многочлена используют величину |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
n |
|
|
|
2 . |
|
|
|
|
|
|
|
m |
|
Pm (xi ) yi |
|
|
|
|
||||||
|
|
|
|
|
n m i 1 |
|
|
|
|
|
|
|
|
||
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
3 |
-0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.4. Графики функций, полученных методом наименьших |
|
||||||||||||||
|
квадратов, для узловых точек {0;0}, {1;0,5}, {2;2}, {3;1,5} |
|
|||||||||||||
За оптимальное значение степени многочлена следует принять то значение m , начиная с которого величина m стабилизи-
руется или начинает возрастать.
5.7. Интерполяция тригонометрическим полиномом
Если требуется провести интерполяцию данных, имеющих периодический характер, то в качестве базисных функций1(x), 2 (x), ..., m (x) следует выбирать периодические функции.
Одним из таких способов является интерполяция тригонометрическим полиномом.
– 106 –
Тригонометрический полином порядка M имеет вид
M |
(x) a0 |
|
M |
|
j |
|
j |
|
|
|
a |
cos jx b |
|||||
T |
|
|
|
sin jx . |
||||
|
2 |
|
j 1 |
|
|
|
|
|
Коэффициенты тригонометрического полинома a j , bj выби-
N
раются из условия минимизации величины Q [TM (xi ) yi ]2 ,
i 1
то есть находятся по методу наименьших квадратов. Для нахождения коэффициентов a j , bj используют соотношения [3]:
|
|
2 |
|
n |
|
|
a j |
|
yi cos jxi , где |
j 0,1,2,..., M , |
|||
|
|
|
||||
|
N i 1 |
|
||||
|
|
|
2 |
n |
|
|
bj |
|
yi sin jxi , где |
j 1,2,..., M . |
|||
|
|
|||||
|
|
|
N i 1 |
|
||
Пример. Дана функция y 5x на интервале [ ; ]. Требу-
ется аппроксимировать ее тригонометрическими полиномами порядка 1, 2, 3. Узловые точки расположены равномерно на данном интервале.
Поскольку функция y 5x – нечетная, то коэффициенты при членах с косинусами равны нулю: a0 a1 a2 a3 0 , поэтому
тригонометрический полином включает только члены с синусами. Расчет коэффициентов bj по приведенной выше формуле дал
следующие значения: b1 9,01891, b2 4,18569 , b3 2,41661.
Уравнения тригонометрических полиномов имеют вид
T1(x) 9,01891sin x ,
T2 (x) 9,01891sin x 4,18569sin 2x ,
T3 (x) 9,01891sin x 4,18569sin 2x 2,41661sin3x .
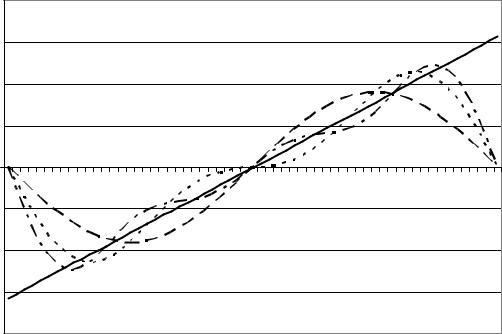
Графики функции y 5x и тригонометрических полиномов
приведены на рис. 5.5.
Видно, что с увеличением степени тригонометрического полинома его график имеет лучшее приближение к прямой y 5x
(см. рис. 5.5).
– 107 –
20 |
|
|
|
|
|
|
15 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-3,14 |
-2,09 |
-1,05 |
0,00 |
1,05 |
2,09 |
3,14 |
-5 |
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
-15 |
|
|
|
|
|
|
-20 |
|
|
|
|
|
|
|
Рис. 5.5. Функция y 5x и тригонометрические |
|
||||
|
|
приближения T1(x) , T2 (x) , T3 (x) |
|
|
||
Значительные отклонения наблюдаются на концах интервала интерполяции, причем чем выше степень полинома, тем ближе к концам интервала начинаются эти отклонения.
5.8. Интерполяция кривой Безье
Кривые Безье появились сравнительно недавно. В 1960 годах Пьер Безье и Поль де Кастельжо, работая в автомобильных компаниях Рено и Ситроен, предложили использовать кривые при проектировании кузовов автомобилей.
Предположим, что имеется n 1 опорных точек. Кривая Безье в параметрическом виде задается выражением [7]:
n |
|
B(t) Pi bi,n (t) , |
0 t 1, |
i 0 |
|
где Pi – функция компонентов векторов опорных точек; bi,n – ба-
зисные функции кривой Безье, называемые также полиномами Бернштейна.
– 108 –

Базисные функции bi,n определяются выражениями
bi,n (t) n ti (1 t)n i ,i
n где i
линома; i Если
( n 3), то
n! – число сочетаний из n по i ; n – степень по- i!(n i)!
– порядковый номер опорной вершины.
кривую Безье строят по четырем опорным точкам в параметрическом виде
B(t) P |
(1 t)3 3P t(1 t)2 |
3P t2 (1 t) P t3 |
, |
t [0;1]. |
||||||||
0 |
|
|
1 |
|
|
|
|
2 |
|
3 |
|
|
В матричной форме кубическую кривую Безье можно запи- |
||||||||||||
сать в виде [7] |
|
|
|
|
|
|
|
P0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
t |
2 |
t |
|
P1 |
|
|
|
|
|
B(t) t |
|
|
1 |
M |
, |
|
|
|||
|
|
|
|
|
|
|
|
|
P2 |
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
3 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
6 |
3 |
|
|
|
|
|
|
|
|
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
||
где M |
|
|
. |
|
|
|
|
|
|
|
|
|
3 |
3 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
||
Несмотря на сложный аналитический вид, итерационная процедура отыскания точек, принадлежащих кривой Безье, очень
простая. |
|
|
|
|
|
Зададим значение параметра t 0,25. На рис. 5.6 |
показан |
||||
процесс нахождения соответствующей точки. |
|
|
|||
Соединим точки P0 и P1 отрезком. Найдем координаты точки |
|||||
P , принадлежащей этому отрезку, из условия | P0P01 | t |
0,25 . |
||||
01 |
|
|
|
| P0P1 | |
|
|
|
|
|
|
|
Повторив подобные действия для пар точек P1 и P2 , P2 и P3 , |
|||||
найдем точки P , P : |
| P1P12 | t 0,25 , |
| P2P23 | t 0,25 . |
|||
12 23 |
| P P | |
| P P | |
|
||
|
1 |
2 |
2 |
3 |
|
|
|
– 109 – |
|
|
|

Теперь повторим все действия сначала, используя в качестве опорных точек P01, P12 , P23 . В результате получим координаты
точек P |
, P : |
| P01P012 | |
|
t 0,25, |
| P12P123 | |
t 0,25. |
|||
| P P | |
| P P | |
||||||||
012 |
123 |
|
|
||||||
|
|
01 |
12 |
|
|
12 |
23 |
|
|
|
P1 |
|
P12 |
|
|
|
P2 |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
P123 |
|
|
P23 |
|
|
|
|
|
|
|
|
|
||
P0123
P01 P012
P0 
 P3
P3
Рис. 5.6. Нахождение точки кривой Безье при t 0,25
Повторив итерационную процедуру в последний раз для опорных точек P012 , P123 , получим координаты точки P0123 , кото-
рая принадлежит кривой Безье: | P012P0123 | t 0,25.
| P012P123 |
Выбрав другое значение параметра t , можно, действуя по описанному выше алгоритму, получить координаты другой точки, принадлежащей кривой Безье. На рис. 5.7 показан процесс определения координат точки при t 0,5.
Множество точек, из которых состоит кривая Безье, можно получить, меняя параметр t в интервале от 0 до 1. На рис. 5.8 показана кривая Безье для четырех точек.
Кривая Безье обладает следующими свойствами:
–она непрерывна;
–располагается внутри фигуры, образованной отрезками, соединяющими опорные точки;
–изменение координат хотя бы одной опорной точки ведет к изменению формы всей кривой;
–110 –
