
Информатика.-7
.pdf
250 |
|
|
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
-50 |
|
|
|
|
|
|
|
|
|
|
|
|
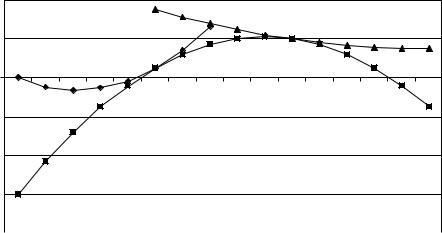
Рис. 5.1. График интерполяционного полинома Ньютона P5 (x) |
||||||||||||
К достоинствам данного метода можно отнести:
меньшую погрешность интерполяции при близко расположенных узлах;
возможность использования вложенных умножений при вычислении значений полинома;
более простой способ получения коэффициентов полинома, чем при интерполяции алгебраическим полиномом.
Недостатком метода можно считать проведение предварительных расчетов коэффициентов полинома. При использовании интерполяционного полинома Лагранжа таких вычислений проводить не нужно.
5.4. Интерполяция параболическим сплайном
Сплайном называется функция, определенная на отрезке [a; b], совпадающая на частичных отрезках [xi ; xi 1] с некоторы-
ми алгебраическими многочленами степени не выше m и имеющая непрерывную (m–1)-ю производную.
Параболическим сплайном называют совокупность многочленов второй степени вида
i (x) ai bi (x xi ) ci (x xi )2 ,
– 91 –
где ai , bi , ci – |
коэффициенты параболических полиномов, |
i 0,1, ..., N 1; |
xi – абсциссы узловых точек, i 0,1,..., N 1; N – |
число узловых точек. |
|
Коэффициенты ai , bi , ci находятся при решении системы линейных уравнений исходя из трех условий:
равенство значений сплайна и аппроксимируемой функции
вузлах (условие Лагранжа): i (xi ) yi , i (xi 1) yi 1;
непрерывность первой производной в узловых точках:
i (xi 1) i 1(xi 1);
равенства некоторому значению D первой производной в начале или на конце интервала: 0 (x0 ) D или N 1(xN ) D.
Первая производная параболического многочлена равна соответственно i (x) bi 2ci (x xi ) .
Таким образом, если имеется N узловых точек, то для интерполяции сплайном будут использованы (N – 1) параболических многочленов. Поскольку каждый многочлен содержит три коэффициента, то общее число неизвестных 3(N 1) . Выполнение
условия Лагранжа дает 2(N 1) уравнений. Поскольку число
внутренних узлов (N – 2), то выполнение для них равенства первой производной дает (N – 2) уравнений. Еще одно уравнение дает выполнение равенства значению D первой производной первого многочлена в начале отрезка интерполяции или последнего многочлена в конце отрезка интерполяции. Общее число уравнений
2(N 1) N 2 1 2N 2 N 1 3N 3 3(N 1),
что соответствует числу неизвестных коэффициентов. Решая данную систему уравнений, можно определить их значения.
Рассмотрим пример нахождения сплайна, если даны следующие значения узловых точек: {0; 0}, {1; 0,5},{2; 2},{3;1,5},
а производная в конце интервала равна нулю.
Поскольку имеются четыре узловые точки, то сплайн состоит из трех параболических многочленов. Общее число неизвестных коэффициентов 9. Выполнение условий Лагранжа определит 6 уравнений системы, два уравнения будут получены при выполнении непрерывности первой производной, одно уравнение по-
– 92 –
лучится за счет равенства нулю первой производной в начале области определения.
В результате получается система, состоящая из 9 уравнений, решая которую, получим значения коэффициентов сплайна:
0 (x0 ) y0 , |
a |
0, |
|
|
|
|
|
|||||
|
0 |
|
|
|
|
|
|
|||||
|
|
(x ) y , |
a0 |
b0 (1 0) c0 (1 0)2 |
|
0,5, |
||||||
|
0 |
|
||||||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
(x ) y |
, |
a1 |
0,5, |
|
|
|
|
|
||||
1 |
1 |
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1(x2 ) y2 , |
|
b1(2 1) c1(2 1) |
2, |
|||||||||
a1 |
|
|||||||||||
|
|
(x2 ) y2 , |
|
|
2, |
|
|
|
|
|
||
2 |
a2 |
|
|
|
|
|
||||||
|
|
(x3 ) y3 , |
|
|
b (3 2) |
c (3 |
2)2 |
1,5, |
||||
2 |
a |
|||||||||||
0 (x1) 1(x1), |
|
2 |
2 |
2 |
|
|
|
|
||||
b |
2c (1 0) b , |
|
|
|
|
|||||||
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
1(x2 ) 2 (x2 ), |
b |
2c (2 1) |
b , |
|
|
|
|
|||||
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
(x3 ) 0 |
|
b |
2c (3 2) 0. |
|
|
|
|
|||
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Значения трех коэффициентов определены: a0 0 , a1 0,5, a2 2 . Подставим их значения в систему и исключим три уравнения:
b |
c |
0,5, |
|
b |
c |
0,5, |
0 |
0 |
c1 2, |
|
0 |
0 |
|
0,5 b1 |
|
b1 |
c1 |
1,5, |
||
|
|
|
|
|
c2 |
0,5, |
2 b2 c2 1,5, |
|
b2 |
||||
|
2c0 b1 , |
|
2c0 b1 , |
|||
b0 |
|
b0 |
||||
|
2c1 b2 , |
|
|
2c1 b2 , |
||
b1 |
|
b1 |
||||
|
2c2 0 |
|
|
2c2 0. |
||
b2 |
|
b2 |
||||
Если из шестого уравнения вычесть третье уравнение, то можно найти значения коэффициентов: c2 0,5, b2 1. Вычи-
тая из пятого уравнение второе уравнение, находим значения
коэффициентов: c1 b1 1,5 2,5, |
b1 1,5 2c1 4 . |
Вычитая |
из четвертого уравнения первое, |
находим c0 b1 |
0,5 3,5, |
b0 0,5 c0 3. |
|
|
– 93 – |
|
|
В результате получаются уравнения параболических много- |
||||||||||||||||||
членов сплайна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(x) 3,5x2 3x |
, при x [x ; x ]; |
|
|
|
|
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
(x) 2,5(x 1)2 |
4(x 1) 0,5 2,5x2 9x 6 при x [x ; x ]; |
|||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
2 |
(x) 0,5(x 2)2 1(x 2) 2 0,5x2 3x 6 при x [x ; x ]. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
На рис. 5.2 показаны графики многочленов параболического |
||||||||||||||||||
сплайна. Видно, как многочлен (x) 3,5x2 |
3x |
в точке |
x 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
плавно перетекает в (x) 2,5x2 9x 6 , а тот в свою очередь |
||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
в точке x 2 |
в многочлен 2 (x) 0,5x2 |
3x 6 . |
|
|
|
|
||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
3 |
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.2. Графики многочленов |
|
|
|
|
|
||||||||
|
|
параболического сплайна 0 (x) , |
1 (x) , 2 (x) |
|
|
|||||||||||||
Представим в общем случае итерационную процедуру нахождения коэффициентов параболических многочленов.
1. Находятся значения hK по формуле hK xK 1 xK при
K 0,1, ..., N 1.
2. Находятся значения zK |
по формуле zK |
|
yK 1 yK |
при |
|
||||
|
|
|
hK |
|
K0,1, ..., N 1.
3.Находятся значения коэффициентов aK , bK , cK параболи-
ческих полиномов при K 0,1, ..., N 1 по следующим формулам:
– 94 –
если |
|
задано значение первой производной D в начале |
|||||||||
интервала |
|
|
интерполяции: |
aK yK , |
bK 2zK bK 1 |
(значение |
|||||
b D ), c |
K |
|
|
bK 1 bK |
; |
|
|
|
|
||
|
|
|
|
|
|
||||||
0 |
|
|
|
|
2hK |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
если |
|
задано значение первой производной D в конце |
|||||||||
интервала |
|
|
интерполяции: |
aK yK , |
bK 2zK bK 1 |
(значение |
|||||
b D ), |
c |
K |
|
bK 1 bK |
. |
|
|
|
|||
|
|
|
|
||||||||
N |
|
|
|
2hK |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Результаты нахождения коэффициентов параболических многочленов сплайна для рассмотренного выше примера (значения узловых точек: {0; 0}, {1; 0,5}, {2; 2}, {3;1,5}) даны в табли-
це 5.3.
Таблица 5.3. Значения коэффициентов многочленов параболического сплайна
|
i |
|
xi |
yi |
hi |
|
zi |
|
ai |
bi |
|
ci |
|
|
0 |
|
0 |
0 |
1 |
|
0,5 |
|
0 |
–3 |
|
3,5 |
|
|
1 |
|
1 |
0,5 |
1 |
|
1,5 |
|
0,5 |
4 |
|
–2,5 |
|
|
2 |
|
2 |
2 |
1 |
|
–0,5 |
|
2 |
–1 |
|
0,5 |
|
|
3 |
|
3 |
1,5 |
|
|
|
|
|
0 |
|
|
|
|
Для получения приближенного значения в точке |
x xi тре- |
|||||||||||
буется |
сначала |
определить, |
к какому |
интервалу принадлежит |
|||||||||
x [xi ; xi 1], затем вычислить значение соответствующего многочлена i (x) .
5.5. Интерполяция кубическим сплайном
Кубическим сплайном называют совокупность многочленов третьей степени вида
i (x) ai bi (x xi ) ci (x xi )2 di (x xi )3,
где ai , bi , ci , di |
– коэффициенты кубических полиномов, |
i 0,1,..., N 1; xi |
– абсциссы узловых точек, i 0,1,..., N 1; N – |
число узловых точек.
– 95 –
Коэффициенты ai , bi , ci , di находятся при решении системы линейных уравнений, удовлетворяющих трем условиям:
равенство значений сплайна и аппроксимируемой функции
вузлах (условие Лагранжа): i (xi ) yi , i (xi 1) yi 1;
непрерывность первой и второй производной в узловых
точках: i (xi 1) i 1(xi 1), i (xi 1) i 1(xi 1);
равенство нулю вторых производных на концах интервала
0 (x0 ) 0 , N 1(xN 1) 0 .
Первая и вторая производные кубического многочлена
i (x) bi 2ci (x xi ) 3di (x xi )2 ,i (x) 2ci 6di (x xi ).
Таким образом, если имеется N узловых точек, то для интерполяции сплайном будут использованы (N – 1) кубических многочленов. Поскольку каждый многочлен содержит четыре коэффициента, то общее число неизвестных 4(N 1) . Выполнение
условия Лагранжа дает 2(N 1) уравнений. Поскольку число
внутренних узлов (N – 2), то выполнение для них равенства первой производной дает (N – 2) уравнений, столько же уравнений дает выполнение равенства второй производной. Еще два уравнения дает выполнение равенства нулю вторых производных на концах отрезка. Общее число уравнений
2(N 1) N 2 N 2 2 2N 2 2N 2 4N 4 4(N 1) ,
что соответствует числу неизвестных коэффициентов.
Решая данную систему уравнений, можно определить их значения.
Рассмотрим пример нахождения сплайна, если даны сле-
дующие значения узловых точек: {0; 0}, {1; 0,5},{2; 2},{3;1,5}.
Поскольку имеются четыре узловые точки, то сплайн состоит из трех кубических многочленов. Общее число неизвестных коэффициентов 12. Выполнение условий Лагранжа определит 6 уравнений системы, два уравнения будут получены при выполнении непрерывности первой производной, еще два уравнения получатся при выполнении непрерывности второй производной,
– 96 –
оставшиеся два уравнения получатся за счет равенства нулю второй производной на краях области определения.
В результате получается система, состоящая из 12 уравнений, решая которую, получим значения коэффициентов сплайна:
0 (x0 ) y0 , |
a |
0, |
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
(x1) y1 , |
a0 |
b0 (1 0) c0 (1 0) |
2 |
d0 (1 0) |
3 |
0,5, |
||||||||||
0 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x1) y1 , |
|
a1 0,5, |
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
(x |
) y |
|
, |
|
b1(2 1) c1(2 1)2 d1(2 1)3 2, |
|||||||||||||
|
2 |
a1 |
||||||||||||||||||
|
1 |
|
2 |
|
|
|
2, |
|
|
|
|
|
|
|
|
|
|
|
||
2 (x2 ) y2 , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
(x |
) y |
, |
a |
b (3 2) |
c (3 2)2 |
d |
|
(3 2)3 1,5, |
||||||||
|
2 |
2 |
||||||||||||||||||
|
|
3 |
|
3 |
|
2 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
(x1) 1(x1), |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
2c0 (1 0) 3d0 (1 0) |
2 |
b1 , |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
b0 |
|
|
|
|||||||||
1(x2 ) 2 (x2 ), |
|
2c (2 1) |
3d (2 1) |
2 |
b |
, |
|
|
||||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
1 |
|
(1 |
1 |
|
|
|
|
2 |
|
|
||
0 (x1) 1(x1), |
2c 6d |
|
0) 2c , |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
(x2 ), |
|
0 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
(x2 ) 2 |
2c1 6d1(2 1) 2c2 , |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
(x |
) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
|
|
|
2c0 6d0 (0 0) 0, |
|
|
|
|
|
|
|
|
||||||
2 (x3 ) 0 |
|
2c 6d |
2 |
(3 |
2) 0. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Значения четырех |
|
коэффициентов определены: a0 0 , |
||||||||||
a1 0,5, |
a2 2 , |
c0 0. Подставим их значения в систему и ис- |
||||||||||
ключим четыре уравнения: |
|
|
|
|
|
|
|
|
||||
|
|
b0 d0 |
0,5, |
|
|
|||||||
|
|
0,5 |
b |
c |
d |
2, |
||||||
|
|
|
|
|
|
1 |
|
1 |
|
1 |
||
|
|
2 b |
c |
d |
2 |
1,5, |
||||||
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
b0 |
|
3d0 b1 , |
|
|
||||||
|
|
|
2c1 3d1 b2 , |
|||||||||
|
|
b1 |
||||||||||
|
|
6d |
0 |
|
2c , |
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
6d1 2c2 , |
|
||||||
|
|
2c1 |
|
|||||||||
|
|
2c |
|
|
6d |
2 |
0. |
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
– 97 – |
|
|
|||
Из последних трех уравнений следует, что |
|
|
||||||||||||||||
|
|
|
|
|
|
|
6d0 6d1 6d2 или d2 |
d0 d1. |
|
|||||||||
Подставим это соотношение в последнее уравнение: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
c2 3d2 3(d0 d1). |
|
|
|
||||
В результате получим систему, состоящую из 8 уравнений: |
||||||||||||||||||
b |
|
0,5 |
d |
|
, |
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
b1 |
c1 d1 1,5, |
|
|
|
|
|
|
|
||||||||||
|
|
|
c2 d2 |
0,5, |
|
|
|
|
|
|
||||||||
b2 |
|
|
|
|
|
|
|
|||||||||||
c |
3d |
0 |
, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
3d2 , |
|
|
|
|
|
|
|
|
|
|
|
||||
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
b0 3d0 |
0,5 d0 3d0 |
0,5 2d0 , |
|
|
|
|||||||||||
b1 |
|
|
|
|||||||||||||||
|
|
|
b1 2c1 |
3d1 0,5 2d0 |
6d0 3d1 |
0,5 8d0 3d1 , |
||||||||||||
b2 |
|
|||||||||||||||||
6d |
0 |
6d 6d |
2 |
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
Подставим соотношения, полученные для b1 , b2 , c1 , c2 , во |
||||||||||||||||||
второе и третье уравнение, получим |
|
|
|
|
|
|||||||||||||
0,5 2d0 3d0 |
d1 1,5, |
|
5d0 d1 1, |
|||||||||||||||
|
|
|
|
|
|
|
3d1 |
3d2 d2 0,5, |
|
|
|
|
2d2 1, |
|||||
0,5 8d0 |
8d0 3d1 |
|||||||||||||||||
|
|
d |
|
d |
|
|
|
|
|
|
|
d |
|
d . |
||||
d |
2 |
0 |
|
|
|
|
|
d |
2 |
0 |
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|||||
Из первого уравнения следует: d1 1 5d0 , из третьего урав- |
||||||||||||||||||
нения видно, что d2 d0 d1 d0 1 5d0 |
4d0 |
1. |
||||||||||||||||
Подставим эти выражения во второе уравнение и найдем значение d0 :
8d0 3(1 5d0 ) 2(4d0 1) 1 15d0 6 d0 0,4.
Тогда d1 1 5 0,4 1; d2 4 0,4 1 0,6 ;
c1 3 0,4 1,2; c2 3 0,6 1,8; b0 0,5 0,4 0,1; b1 0,5 2 0,4 1,3; b2 0,5 8 0,4 3 ( 1) 0,7.
В результате получаются уравнения кубических многочленов сплайна:
– 98 –
(x) 0, 4x3 |
0,1x , |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) (x 1)3 1,2(x 1)2 |
1,3(x 1) 0,5, |
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 (x) 0,6(x 2)3 1,8(x 2)2 |
0,7(x 2) 2 . |
|
|
||||||||||||||
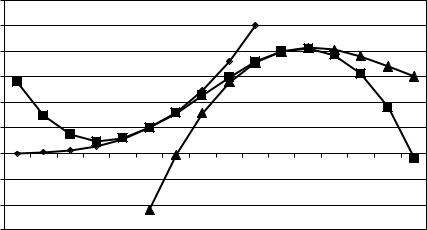
На рис. 5.3 показаны графики многочленов кубического |
|||||||||||||||||
сплайна. Видно, как многочлен (x) 0,4x3 |
0,1x |
в точке x 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
плавно перетекает в |
(x) (x 1)3 |
1,2(x 1)2 |
1,3(x 1) 0,5, |
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x 2 |
в |
|
многочлен |
|
а тот |
в |
свою |
|
очередь |
в |
|
точке |
|
|
||||||||
2 (x) 0,6(x 2)3 1,8(x 2)2 0,7(x 2) 2 . |
|
|
|
|
|||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,5 |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.3. Графики многочленов |
|
|
|
||||||||||
|
|
|
кубического сплайна 0 (x) , |
1 (x) , |
2 (x) |
|
|
||||||||||
В общем случае итерационная процедура нахождения коэффициентов кубических многочленов следующая.
1. Находятся значения hK по формуле hK xK 1 xK при
K 0,1, ..., N 1.
2. Находятся значения gK |
по формуле gK |
|
yK 1 yK |
при |
|
||||
|
|
|
hK |
|
K0, 1, ..., N 1.
3.Находятся значения uK по формуле uK 6(gK gK 1) при
K1, ..., N 1.
4.Находятся значения mK при решении системы линейных
уравнений
– 99 –
2(h h )m h m u , |
|
||||||
|
0 |
1 |
1 |
1 |
2 |
1 |
|
hK 1mK 1 |
2(hK 1 |
hK )mK hK mK 1 uK , |
K 2,3,..., N 2, |
||||
|
|
|
2(hN 2 hN 1)mN 1 uN 1. |
|
|||
hN 2mN 2 |
|
||||||
5.Принимается m0 mN 0.
6.Находятся значения коэффициентов aK , bK , cK , dK кубических полиномов при K 0, 1, ..., N 1 по следующим формулам:
aK yK , |
cK mK , dK |
mK 1 mK |
, |
||||
|
|
||||||
|
|
|
2 |
|
6hK |
||
b |
g |
K |
|
hK (2mK mK 1) |
. |
||
|
|||||||
K |
|
|
6 |
|
|
||
|
|
|
|
|
|
||
Результаты нахождения коэффициентов кубических многочленов сплайна для рассмотренного выше примера (значения узловых точек: {0; 0}, {1; 0,5}, {2; 2}, {3;1,5}) даны в таблице 5.4.
Таблица 5.4. Значения коэффициентов многочленов кубического сплайна
i |
xi |
yi |
hi |
gi |
ui |
mi |
ai |
bi |
ci |
di |
0 |
0 |
0 |
1 |
0,5 |
|
0 |
0 |
0,1 |
0 |
0,4 |
1 |
1 |
0,5 |
1 |
1,5 |
6 |
0,5 |
0,5 |
1,3 |
1,2 |
–1 |
2 |
2 |
2 |
1 |
–0,5 |
–12 |
2 |
2 |
0,7 |
–1,8 |
0,6 |
3 |
3 |
1,5 |
|
|
|
|
|
|
|
|
Для получения приближенного значения в точке x xi , так-
же как и в случае с параболическим сплайном, требуется сначала определить, к какому интервалу принадлежит x, после чего вычислить значение соответствующего кубического многочлена
i (x) .
5.6. Метод наименьших квадратов
При проведении исследований часто получают совокупность узловых точек {x1; y1}, {x2; y2},…, {xN ; yN }, про которые априор-
но известно, что они определены с экспериментальной погреш-
– 100 –
