
Дополнительные главы математики.-2
.pdf
ЛЕКЦИЯ 5. 09.04.2019 § 4. Свёртка оригиналов, интегральные уравнения.
Определение. Свёрткой двух оригиналов называется функция
f
tg
0
f ( )g(t )d
.
Пример. Найти свёртку t t .
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
2 |
t |
|
|
3 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
g (t )d |
|
= (t |
|
|
|
|
|
|
|
|
||||||||||||||
Решение. f |
|
2 |
)d = t |
|
|
|
|
= |
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
3 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
t 2 |
|
t3 |
|
1 |
|
1 |
3 |
|
1 |
t3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
t |
|
|
= |
|
|
t |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
3 |
|
2 |
|
|
3 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ. |
t t |
1 |
t |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема об основном свойстве свёртки. |
L( f |
g) F ( p)G( p) . |
|||||||||||||||||||||||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
L( f g) |
( f |
g)e |
pt |
dt |
= |
|
|
f ( )g(t )d |
|
e |
pt |
dt |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
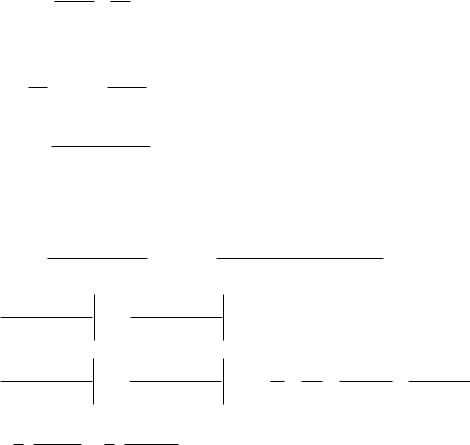
Исследуем получившийся двойной интеграл. Начертим область
интегрирования.
51

При каждом t |
изменение |
|
происходит от 0 до t . Если изменить |
порядок интегрирования, то при каждом |
движение точки внутри |
|
выделенной области будет происходить от |
до (горизонтальная |
|
линия). |
|
|
t |
|
|
|
|
pt |
|
||
|
|
|
f ( )g(t )d |
|
|
dt |
||
|
e |
|
||||||
0 |
|
0 |
|
|
|
|
|
|
|
|
pt |
|
|
|
|||
|
|
|
f ( )g(t )e |
|
|
|
||
|
|
|
dt d |
|||||
0 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
0 |
|
|
= |
|
|
|
|
0 |
t |
|
|
|
|
f ( )g(t )e |
||
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
g(t )e |
|
|
||
f ( ) |
|
||
|
|
|
|
pt
pt
d dt
dt d
=
(сменив порядок, вынеесли из внутреннего интеграла множитель, не зависящий от t ). Во внутреннем интеграле, можно применить
свойство (теорема запаздывания) |
L( f (t a)) e |
pa |
F( p) . |
|
|
f ( ) G( p)e |
|
d |
|
|
p |
= G( p) |
||
|
||||
0 |
|
|
|
0 |
Что и требовалось доказать.
Обратимся снова к примеру,
f ( )e |
p |
d |
= G( p)F |
|
который был выше:
( p)
t
=
t
F (
1 |
t |
|
6 |
||
|
p)G( p)
3 |
. |
|
.
Попробуем сопоставить преобразования правой и левой части.
L(t t) |
= |
L(t) L(t) |
= |
|
1 |
|
||||||||||||
p |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
3 |
|
|
1 |
L t |
3 |
= |
1 |
|
|
|
3! |
|||||
L |
|
t |
|
= |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4 |
||||||||
6 |
|
|
|
|
6 |
|
|
|
6 |
|
|
p |
||||||
Результаты совпадают.
1 |
|
p |
2 |
|
|
=
=
1
p4
1 |
|
p |
4 |
|
|
.
52

Следствие. Свёртка симметрична:
f g g f
.
Это следует из того, что для произведения коммутативность
выполняется: |
G( p)F ( p) = F ( p)G |
Следствие. Формула Дюамеля.
( p)
L(
.
f g) ( pF ( p)
f
(0))G(
p)
.
Следует из предыдущей теоремы и свойства дифференцирования оригинала.
Пример. Найти t sin t .
Решение. Рассмотрим 2 способа и убедимся, что будет одно и то же:
1)прямое нахождение свёртки по определению (через интеграл),
2)через обратное преобразование.
Способ 1). Так как свёртка симметрична, то мы можем в любом из
двух элементов записать
t
, в каком удобнее.
t sin t
|
t |
= |
|
|
|
|
0 |
(t )sin( )d
=
t t sin( )d
0
t sin( )d
0
, во втором
интегрирование «по частям»:
u
,
u
1
,
v sin
, v cos ,
t |
t |
|
|
|
|
|
|
t |
|
t sin( )d sin( )d = |
t |
|
|
t |
|
|
|||
|
|
cosd |
|||||||
tcos 0 |
cos |
0 |
|||||||
0 |
0 |
|
|
|
|
|
|
0 |
|
tcos t |
cos t |
sin t |
= t(cost |
1) cos t |
sin t |
||||
0 |
0 |
|
0 |
|
|
|
|
0 |
0 |
t(1 cost) t cost (sin t) |
= t sin t . |
|
|
|
|
|
|||
|
|
|
|
53 |
|
|
|
|
|
=
=

Ответ.
t sin t
t sin t
.
Способ 2). Найдём преобразование Лапласа от свёртки как произведение преобразований от каждой части. А затем обратное преобразование.
L(t sin t) = L(t) L(sin t) =
1 |
|
||
p |
2 |
||
|
|||
|
|
||
|
1 |
|
p |
2 |
1 |
|
||
.
Обратное преобразование с помощью вычетов:
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pt |
pt |
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
||||||
Re s |
|
|
|
|
|
|
= |
e |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
e |
|
|
|
|
|
= |
||||
p2 ( p2 |
1) |
|
1 |
|
|
p2 ( p i) |
|
p2 ( p i) |
|
||||||||||||||||||||||||||
|
|
|
|
p2 |
|
|
|
|
p i |
|
p i |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
te |
pt |
( p |
2 |
1) |
2 pe |
pt |
e |
it |
|
|
|
|
e |
it |
|
|
|
t |
|
|
e |
it |
|
e |
it |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= t |
sin |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
( p |
2 |
1) |
2 |
|
( 1)2i |
( 1)( 2i) |
1 |
|
2i |
2i |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
p 0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ. |
t sin t t sin t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Найти свёртку e cost . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Решение. Сделаем это через обратное преобразование Лапласа. |
|
||||||||||||||||||||||||||||||||||
L(et cost) |
= L(et ) L(cos t) |
= |
|
1 |
|
|
|
|
p |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
p2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Обратное преобразование с помощью вычетов.
t
.
Re s |
pe |
pt |
|
|
|
|
|
||
( p 1)( p |
2 |
1) |
||
|
|
|||
= |
pe pt |
|
|
|
pe pt |
|
|
pe pt |
|
p2 1 |
p 1 |
( p 1)( p i) |
p i |
( p 1)( p i) |
p i |
||||
|
|
|
|
|
|
|
|||
54

=
e |
t |
|
ie |
it |
|
ie |
it |
|
|
|
|
|
|
||||
|
|
i)(2i) |
( 1 |
i)( 2i) |
||||
2 |
( 1 |
|
||||||
в последней дроби сократим два
минуса, а затем в двух последних сократим на знаменателю.
i
и приведём к общему
|
e |
t |
|
|
( 1 i)e |
it |
|
|
|
|
|
|
( 1 i)e |
it |
|
|
|
e |
t |
|
( 1 i)e |
it |
|
( 1 i)e |
it |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
||||||||||||||||||||||||
|
|
|
( 1 i)( 1 i)2 |
|
( 1 i)( 1 i)2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
4 |
|
||||||||||||||||||||||||||
|
et |
|
eit |
|
|
e it |
|
|
ieit |
ie it |
|
|
|
et |
|
1 eit |
e it |
|
|
eit |
|
|
e it |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
2 2 |
|
|
2 |
|
|
|
|
4i |
|
|
4i |
|
|||||||||
|
e |
t |
|
1 |
|
|
|
|
1 e |
it |
|
e |
it |
|
e |
t |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
e |
t |
sin t cost . |
|||||||||||
|
|
|
cost |
|
|
|
|
= |
|
|
cost |
sin t |
= |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
2 |
2 |
|
|
|
2i |
|
|
|
2 |
2 |
2 |
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ответ. e |
t |
cost |
|
|
1 |
e |
t |
sin t cost . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=
Преобразование Лапласа и интегральные уравнения.
Если в уравнении участвует интеграл с переменным верхним пределом, то в некоторых случаях можно представить его как свёртку каких-то функций. Тогда можно от интегрального уравнения перейти к алгебраическому, применив преобразование Лапласа к правой и левой части.
Пример. Решить интегральное уравнение
t(t) sin t (t ) ( )d
0
.
Решение. Обозначим преобразование функции через (
В интеграле - свёртка и линейной функции 1-й степени.
Тогда после преобразования Лапласа получим:
p)
.
55
( p) |
1 |
|
||
2 |
1 |
|||
p |
|
|||
|
|
|||
1 |
|
p |
2 |
|
|
( p)
.
Это уже алгебраическое уравнение, а не интегральное.
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
p |
2 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
2 |
|
( p) |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
p |
|
|
|
|
|
|
|
|
p |
1 |
|
|
|
|
p |
|
|
|
|
p |
1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
( p |
1)( p |
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Теперь ищем обратное преобразование Лапласа. По знаменателю |
|||||||||||||||||||||||||||||||||||||||||||||
видно, что функция имеет 4 полюса порядка 1. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
e |
pt |
|
|
|
|
|
|
|||
Re s |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
= Re s |
|
|
|
|
p |
|
|
|
|
= |
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
( p |
1)( p |
1) |
|
|
|
|
|
|
|
|
( p 1)( p 1)( p i)( p i) |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
p |
2 |
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
( p 1)( p |
2 |
1) |
|
|
|
|
( p 1)( p |
2 |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
p |
1 |
|
|
|
|
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
p |
2 |
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
e |
pt |
|
|
|
|
|
t |
|
|
e |
t |
|
e |
it |
|
e |
it |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
= |
e |
|
|
|
|
|
|
|
|
|||||||||||||
( p i)( p |
2 |
1) |
|
|
|
|
( p i)( p |
2 |
1) |
4 |
|
4 |
(2i)( 2) |
( 2i)( 2) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
p |
i |
|
|
|
|
|
p i |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
t |
|
e |
t |
|
|
1 |
|
|
e |
it |
e |
it |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= sht sin t . |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2i |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ. |
|
1 |
|
sin t sht . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
Пример 2. Решить интегральное уравнение |
(t) t et ( )d . |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Решение. В интеграле - свёртка
и экспоненты. Тогда
56
|
|
|
t |
|
|
|
|
|
|
(t) t |
|
e |
t |
( )d |
|
||||
|
|||||||||
|
|
||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
( p) |
|
2 |
|||||
|
|
p 1 |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
||
( p) |
1 |
|
|||
p |
2 |
||||
|
|
|
|||
|
|
|
|
||
p 2 |
( p) |
||||
p 1 |
|||||
|
|
|
|
||
1 p
1 |
|
p |
2 |
|
|
( p 1
(
)
p
|
|
|
|
) |
p 1 |
|
|
( p 2) p |
2 |
||
|
|||
|
|
.
Ищем обратное преобразование.
|
|
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
(t) Re s |
( p 1)e |
pt |
|
|
||||||||||||||||||
( p) |
|
|
|
|
|
|
|
|
|
|
= |
|
|||||||||||||||||||||||||
( p 2) p |
2 |
|
( p 2) p |
2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
( p 1)e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p 2 |
|
|
|
|
|
|
p 0 |
|
|
|
|
|
|
|
|
p 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pt |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1( p 2) 1( p 1) |
|
|
|
p 1 |
|
|
|
|
( p |
1)e |
|
||||||||||||||||||||||||||
e pt |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
tept |
|
|
|
|
|
2 |
|
|
||||||
|
|
( p |
2) |
|
|
|
|
|
|
|
|
|
p 2 |
|
|
|
|
|
|
p |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 0 |
|
|
|
|
|
p 2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
1 |
|
|
|
|
|
e |
2t |
|
|
|
|
t |
|
|
1 |
|
|
e |
2t |
|
|
|
|
|
|
|
|
|
|
|
||||
|
t |
|
|
|
|
|
= |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
4 |
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
t |
|
|
|
1 |
|
|
e |
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ. |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
=
57
ЛЕКЦИЯ 6. 23.04.2019
ГЛАВА 4
Дифференциальные уравнения в частных производных
(УМФ - уравнения математической физики)
Во 2 семестре мы изучали дифференциальные уравнения,
содержащие функцию одной переменной. Однако при изучении физических процессов часто появляются дифференциальные уравнения с функциями от нескольких переменных, а значит, с
частными производными. Переменные, соответствующие положению
в пространстве |
x, y, z , и время |
t . Даже если рассматривается |
одномерное пространство, всё равно уже будет 2 переменных x,t .
Выведем 2 основных типа уравнений: волновое и теплопроводности (диффузии).
Пусть функция u(x, t) задаёт отклонение некоторой натянутой струны от положения равновесия в точке с абсциссой x в момент времени t .
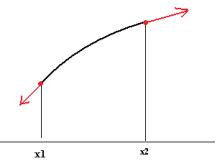
Рассмотрим небольшой участок струны, и все силы, действующие на него. Во-первых, вспомним, что ускорение пропорционально
58

суммарной силе, действующей на участок. Рассмотрим проекцию ускорения и сил на вертикальную ось. Ускорение в точке
определяется 2-й производной,
|
2 |
u |
|
||
t |
2 |
|
|
||
. Тогда суммарное ускорение,
действующее на участок от
x1
до
x2
, равно
x |
|
2 |
|
2 |
u |
||
|
|
||
t |
2 |
||
x |
|
||
|
|
|
|
1 |
|
|
|
dx
.
Также в каждой точке действует некоторая внешняя сила
|
x |
|
|
2 |
|
Её действие на участок определяется интегралом |
|
f (x, |
|
||
|
x |
|
|
1 |
|
f (x, t)dx
t)
.
.
Кроме
того, действует сила натяжения. Её проекция на вертикальную ось определяется проекцией суммы двух сил (показанных красными стрелками на чертеже). Если данный участок не прямолинейный, то
угол наклона |
в |
точках |
x1 |
и |
x2 |
немного |
разный. Проекция |
пропорциональна |
синусу угла наклона. Вспомним также, что для |
||||||
бесконечно |
малой величины |
x , |
верны |
эквивалентности: |
|||
sin x tgx x . В точке x2 , тангенс угла наклона ux (t, x2 ) , в точке
x1
,
u
соответственно, x (t, x1 ) . Сумма сил натяжения, действующих
на участок, равна
u |
(t, x |
|
) |
u |
(t, x |
) |
|
2 |
|
||||
x |
|
|
x |
1 |
|
|
|
|
|
|
|
(разность, потому что в левой
точке сила направлена в противоположную сторону). Эта разность может рассматриваться как результат применения формулы Ньютона-
Лейбница при интегрировании по переменной x . А именно,
59

u |
|
|
|
u |
|
u |
|
x |
2 |
|
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
u |
|
|
|
|
|
|
|
|
|
||||||
(t, x2 ) |
(t, x1 ) = |
(t, x) |
|
|
|
|
= |
|
|
dx . |
Запишем взаимосвязь |
||||||||||||||
x |
x |
x |
|
|
|
|
x |
2 |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
|
|
|
|
|
|
|
x |
|
2 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
2 |
u |
|
|
|
|
|
|
2 |
u |
|
2 |
|
||||
ускорения и суммарной силы: |
|
|
|
|
= |
a |
2 |
|
|
+ |
|
f (x,t)dx , |
|||||||||||||
|
|
|
2 |
dx |
|
|
2 dx |
||||||||||||||||||
|
t |
|
x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
x |
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
где |
a |
2 |
некоторый коэффициент, |
|
зависящий от плотности струны. |
||||||||||||||||||||
|
|
||||||||||||||||||||||||
Почему он положительный? При изгибе вверх, 2-я производная отрицательна (вспомним взаимосвязь выпуклости графика вверх и 2
производной), и при этом сила тоже действует вниз. При изгибе вниз,
наоборот, 2-я производная положительна, но и сила направлена вверх.
Таким образом, |
коэффициент заведомо положительный, и мы сразу |
|||||||||||||||||||
обозначаем его a |
2 |
, чтобы подчеркнуть данный факт. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
Если перейти к пределу при x2 x1 , то получим равенство в точке: |
|
|||||||||||||||||||
|
2 |
u |
|
|
|
2 |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
|
f (x,t) |
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
, или в других обозначениях, |
utt |
a |
uxx f . |
|
|||||||||
t |
2 |
|
x |
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Это называется волновое уравнение, или уравнение колебаний. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Если внешние силы отсутствуют, то |
utt a |
|
uxx . |
|
|
|
|
|
||||||||||||
Рассмотрим аналог условий Коши для этого уравнения. |
|
|
|
|
||||||||||||||||
Если концы |
|
|
струны |
закпеплены, |
то |
u(0, t) 0 |
и |
u(l, t) 0 |
- |
|||||||||||
граничные условия. |
Кроме того, в момент времени |
t 0 должны |
||||||||||||||||||
быть заданы |
|
начальные условия |
u(x,0) |
|
, определяющие |
|||||||||||||||
|
и ut (x,0) |
|||||||||||||||||||
положение точек струны в нулевой момент времени и их скорости.
60
