Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Дополнительные главы математики.-2

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.6 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Ещё преобразование Фурье обозначается так:

F( )

Ф f

(

Пример. Найти пр. Фурье для

	0
f (x)	3x
e

x ( , A) x ( A, )

Решение. F ()

f (x)e

i x

(3 i

) x

(3 i

) x

)

0 e

(3 i

) A

(3 i

) A

3 i

(3 i ) A

Ответ.

F( )

2 (3 i )

			i x
e	3x	e	i x	dx
e		e		dx
A

=
A

(3 i ) A

Найдём ещё и обратное преобразование от

F( )

2 (3 i )

(3 i ) A

i x

f (x)

F ( ) e

i x

d =

(3 i )

e (3 i ) A

i x

Заметим,

что везде

присутствует

3 i

произведение

при этом d

, поэтому логично ввести замену переменной

z i ,

dzi . Таким образом, мы будем вычислять интеграл по

вертикальной (мнимой) оси, причём единственная особая точка этой

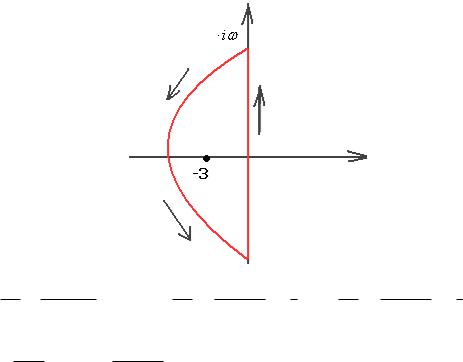
функции - полюс 1-го порядка

z 3

, слева от этой оси. Для

замкнутого контура, по свойствам вычетов получаем, что интеграл равен произведению 2 i на вычет функции в точке 3 . В пределе,

интеграл по вертикальной оси равен

на сумму вычетов в левой

полуплоскости, а там всего одна особая точка, а именно,

3 .

1	e	(3 i ) A		i x
			e		d
2		3 i

(3 z) A

3 z

	1				e	(3 z) A
=			2	i Re s			e	zx
								zx
	2	i				3 z
				z 3
				z 3

lim e (3 z) Ae zx = e0e 3x z 3

= e

Как видим, от точки

результат вообще не зависит.

Интеграл Фурье в действительной форме, его вывод из

интеграла Фурье в комплексной форме.

i u

Снова запишем интеграл

f (x)

f (u)e

внесём экспоненту из внешнего интеграла во внутренний.

x	d

Тогда:

i ( x u)

f (x)

f (u)e

Преобразуем экспоненту по формуле Эйлера.

f (x)

f (u) cos( (x u)) if (u) sin(

(x u))du

1
	f (u) cos( (x u))du	d
2	f (u) cos( (x u))du	d
2

i
	f (u) sin( (x u))du	d
2	f (u) sin( (x u))du	d
2

Но во 2-м интеграле функция sin нечётна по переменной , а

интеграл по всей оси , следовательно, он равен 0, и в итоге остаётся

выражение:

	f (x)	1
	f (x)	2
		2


		f

(u) cos(x

u)du d

В то же время, функция cos чётна по переменной , т.е. можно записать интеграл только по правой полуоси и удвоить его:

	1
f (x)			f (u) cos(x u)du	d
f (x)			f (u) cos(x u)du	d

		0

Далее заметим, что косинус разности преобразуется по формуле: cos(a b) cos a cos b sin a sin b .

	1
f (x)			( f (u) cos(x) cos(u)	f (u) sin( x) sin( u))du	d
f (x)			( f (u) cos(x) cos(u)	f (u) sin( x) sin( u))du	d

		0

	1			1
		( f (u) cos( u))du	cos( x)
		( f (u) cos( u))du	cos( x)

0



( f (u) sin( u))du sin( x)		d

Таким образом, мы представили в виде:

f (x) (a( ) cos x b( ) sin x)d где коэффициенты:

	a( )	1
	a( )


	f (u) cos udu

	b()	1
	b()


	f

(u) sin udu

Получился вид интеграла Фурье, очень похожий на тригонометрический ряд Фурье, с тем отличием, что частота здесь не дискретна, а непрерывна. Это действительная форма интеграла Фурье.

то

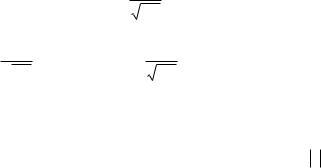
Если ввести в рассмотрение величину A()	a	2	() b	2	() ,

a( ) A( ) cos( ) , b( ) A( ) sin ( ) . Можно представить

себе эти величины как 2 катета и гипотенузу прямоугольного

треугольника.


Тогда интеграл			f (x)		(a( ) cos x b( ) sin x)d
Тогда интеграл			f (x)		(a( ) cos x b( ) sin x)d
				0
		A( ) cos( ) cos x sin ( ) sin x d
виде f (x)
виде f (x)
	0

			f (x) A( ) cos(x ( ))d
					0

запишется в

Здесь A(

интеграла

) - амплитуда,

Фурье.

( )

- фаза. Это гармонический вид

Свойства преобразования Фурье.

Перечислим несколько основных свойств.

Свойство 1. Линейность.

Ф af (x) bg(x)

aF( )

bG( )

Доказательство. Следует из линейности интеграла.

Ф af

a 2

(x)

	f (

bg(x)
x)e	i x

1
1	(af (x) bg
2	(af (x) bg
2

	b		i
	b	g(x)e	i
	2	g(x)e
	2

(x))
x	dx

e	i

x	dx	=

aF ( ) bG( ) .

Свойство 2. Свойство подобия. Ф f (ax)	1
		F	.

	a	a

Доказательство.

Ф f (ax)

1 2


	f (ax)e

x	dx

. Нужно получить

такой вид, в котором под знаком функции одна переменная. Поэтому

введём замену

, тогда

dt a

. Если

a 0

то

t ( , )

i t

f (t)e

dt =

f (t)e

i a t dt =

Тогда

a 2

1 a

F a

 

А если a 0, то t ( , ) , и тогда, чтоб вернуть обратно правильный порядок (по возрастанию переменной) надо будет добавить лишний минус.

	1
			f (t)e
	2

i t	1
a	1	dt
a
	a
	a

	1		i t

		f (t)e	a	dt
			a
a	2
a	2

=F .

a a

Если a 0, то есть минус, если a 0 то нет. В итоге этот

коэффициент в любом случае положителен, и можно записать одним

способом:	1
способом:		F		.
	a	a
Свойство 3.		Сдвиг по аргументу x .
Доказательство. Ф f (x a) =							1
							1
							2



			1			i (t a) dt
t x a , тогда			1		f (t)e			=

				2
				2

Ф f (x a) e

f (x a)e			i x	dx
f (x a)e				dx
1
1		f (t)e i

	2
	2

i a F ( )

. Замена

t e i a dt =

e	i a	1
e		2
		2

Свойство

	i t
f (t)e	i t	dt	=

4. Сдвиг по .

e	i a	F ( )

Ф[e	iax	f

(x)] F ( a)

Доказательство.				F (
1		i x
	f (x)e		e	iax	dx
2

) =

1 2

1
1			f
2			f
2

	e		f
	e	iax	f
		iax

(x)e	i( a)			x

(x) e		i x	dx

Ф[e	iax

(x)]

Свойство 5. Дифференцирование по

. Если

f (x) непрерывна на

оси, и

lim

f (x) 0

то

Ф f

(x) i F( ) .

i x

Доказательство.

dx . Здесь можно

Ф f (x)

(x)e

применить интегрирование по частям, принимая

u e i x

f (x)

u i e

i x

f (x)

i x

f (x)e

i x

f (x)e

(0 0) i f (x)e

dx =

dx = i F ( ) .

Свойство 6. Дифференцирование по

Ф ixf (x)

F ( )

Доказательство. Применим обычное дифференцирование по параметру, изученное ранее в главе «интегралы от параметра».

F (

1 2

) =

	f

1		f (x)e i x				dx
1

	2

(x)( ix)e			i x	dx	=	1
(x)( ix)e				dx	=	2
						2


=	1		f (x) e		i

		2
		2

				i x
	( ixf (x))e			i x	dx
	( ixf (x))e				dx

x dx =

= Ф ixf

(

Некоторые другие свойства выведем на практике в качестве задач.

Синус-преобразование и косинус-преобразование Фурье.

Пусть функция в интеграле Фурье чётная. Тогда в записи


f (x) (a(
	0
	1
a( )	1	f
a( )		f

) cos x b(

(u) cos udu ,

) sin x)

b()

	d		, где
	1
			f (u) sin udu

второе слагаемое равно 0, так как коэффициент b

произведение чётной f и нечётной функции sin.

() содержит

То есть, в

( f (u) cos( u))du

cos( x)

( f (u) sin( u))du

sin( x)

остаётся только 1-е слагаемое:

f (x)

( f (u) cos( u))du cos( x)d ,

но ведь при этом интеграла по всей

f (u)

оси

cos(u) чётная функция, и можно вместо записать удвоенный интеграл по полуоси:

f (x)


		( f

0	0

(u) cos(u))du cos(x)d

Аналогично, если функция					f (x) нечётная, то исчезает 1-е слагаемое,
остаётся:
		2
	f (x)				( f (u) sin( u))du	sin( x)d
	f (x)				( f (u) sin( u))du	sin( x)d
			0	0
Если функция	f (x) задана только на правой полуоси, то можно

образовать её продолжение на всю ось двумя способами: чётное или нечётное продолжение. И получится то одна, то другая из формул,

представленных выше.

Если в этих формулах тоже распределить равномерно коэффициент между двумя частями двойного интеграла, то:


	2		2
f (x)
						( f (u) cos( u))du cos( x)d
		0			0
							или

	2			2
f (x)
							( f (u) sin( u))du sin( x)d
		0			0

Внутренние интегралы, которые здесь получаются, называются:


	2
1) косинус-преобразованием Фурье: Fс ( )			f (u) cos( u)du ,

		0

2) синус-преобразованием Фурье:

		2
s	()	2
F	()
			0
			0

(u) sin( u)du

Для чётной функции её преобразование Фурье совпадает с косинус-

преобразованием, а для нечётной - с синус-преобразованием. А для функции, заданной только на полуоси, можно построить как синус-

так и косинус-преобразование Фурье.

ЛЕКЦИЯ 3. 12.03.2019

Глава 3. Преобразование Лапласа.

§ 1. Определения и примеры.

Определение. Функция f (t) называется оригиналом, если:


1)	f (t) 0	при t ( ,0) .
2)	f (t) Me		st	, s	называется порядком роста.

3) функция имеет не более конечного числа разрывов, причём они устранимые или 1-го рода, но не 2-го рода.

Объяснение, почему невозможны разрывы 2 рода.

возрастание к		в окрестности точки быстрее, чем

бы условие на порядок роста.

В этом случае e st , нарушалось

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023258.08 Кб2Дополнительные главы информатики-2..pdf
#
05.02.2023650.24 Кб1Дополнительные главы макроэкономики..pdf
#
05.02.2023428.66 Кб3Дополнительные главы математики. Математические модели в экономике-1.pdf
#
05.02.2023371.47 Кб6Дополнительные главы математики. Математические модели в экономике.pdf
#
05.02.2023324.51 Кб1Дополнительные главы математики.-1.pdf
#
05.02.20231.6 Mб1Дополнительные главы математики.-2.pdf
#
05.02.20231.98 Mб1Дополнительные главы математики..pdf
#
05.02.2023827.15 Кб0Дополнительные главы микроэкономики.-1.pdf
#
05.02.20231.1 Mб2Дополнительные главы микроэкономики..pdf
#
05.02.20232.38 Mб8Еnglish for students of Engineering Faculties (basic level)..pdf
#
05.02.2023122.97 Кб3Жанровая организация PR-текста.-1.pdf