Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика.-5

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

3.03 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 205 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

dx rt

– рациональная функция от следовательно, и интеграл от

14x2 54x 43

dx 2

2x 1

(x2 2x 2)(x 5)2

x 5

(x 5)2

x2 2x 2

2 ln

x 5

ln( x2 2x 2) arctg(x 1) C.

x 5

2x3 6x2 4

Пример 4. Найти

dx .

(x2

1)2 (x 1)

Корни знаменателя –

x1 1 кратности 1 и два комплекс-

ных корня x2,3,4,5 i

кратности 2.

Поэтому подынтегральная

функция может быть представлена в виде

2x3 6x2 4

x N

(x2 1)2

(x 1)

x2 1

(x2 1)2

Дальнейшие вычисления предлагается проделать самостоятельно.

2.2.5. Интегрирование простейших иррациональностей и выражений, содержащих тригонометрические функции

Материал этого пункта даётся для справки и является необязательным.

Рациональной функцией переменных x1 , x2 ,...,xn назовём

отношение двух полиномов от этих переменных, или, что то же самое, отношение двух линейных комбинаций всевозможных произведений целых степеней этих переменных.

Пусть R x, r1 x , r2 x ,...,rn x x, r1x, r2 x,...,rnx. Эта функция, а

неё, рационализируется подстановкой x t r , где r – наименьшее общее кратное чисел r1 , r2 ,...,rn . Тогда dx rt r 1dt и Тогда

r 1dt и, подставляя x и dx в подынтегральное выражение, получаем под интегралом рациональную функцию аргумента t. Аналогично, если подынтегральное выражение

ax b

R x, r1

, r2

,..., rn

есть

рациональная

функция

cx d

от x, r1

ax b

, r2

ax b

,...,rn

ax b

, то подынтегральная функция

cx d

рационализируется подстановкой

ax b

t r , где r –

наимень-

cx d

шее общее кратное чисел

r , r ,...,r . Тогда x

dt r b

. Под-

1 2

ct r a

ставляя в исходное выражение, получаем рациональную функцию от t.

Пример 1. Вычислить

dx.

x 3 x2

Наименьшее общее кратное чисел 2 и 3 равно 6. Поэтому

делаем замену x t 6 . Тогда dx 6t 5dt , и

t 3 6t 5dt

t 4

dt 6

t 4 1 1

x 3

t 6 t 4

t 2 1

6 (t 2 1)dt 6

6 (t 2 1)dt 3

t 2 1

t 1

2t3 6t 3ln

t 1

3ln

t 1

C 2t 3 6t 3ln

t 1

x 1

2 x 6

6 x 3ln

x 1

Пример 2. Вычислить

5 (x 2)3

dx .

x 2 5 (x 2)8

Наименьшее общее кратное чисел 2 и 5 равно 10. Поэтому делаем замену x 2 t10. Тогда dx 10t9dt , и

5 (x 2)3

t 610t9dt

t5 t16

(x 2)8

x 2

10 ln

C 10 ln

1 t11

1 (x 2)

Пример 3.

4 x 1 1

dx.

x 1 4

(x 1)

Наименьшее общее кратное чисел 2 и 4

делаем замену x 1 t 4 . Тогда dx 4t 3dt , и

(t 1)4t3dt

4 x 1 1

t 2 t3

(x 1)3

x 1

4 tdt 2t 2 C 2

x 1 C.

t10

1 t11 dt

равно 4. Поэтому

Для	интегрирования рациональных			функций вида
R(sin x,cos x)	применяют подстановку	t tg	x	, которая называ-
			2

ется универсальной тригонометрической подстановкой. Тогда

x 2arctgt, dx

2dt

,sin x

, cos x

1 t 2

К сожалению,

t 2

универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому по возможности пользуются

следующими

подстановками.

Если

R( sin x,cos x) R(sin x,cos x) ,

то делают замену

cos x t , и

тогда sin xdx dt. При

R(sin x, cos x) R(sin x,cos x)

полага-

ют

sin x t ,

при

этом

cos xdx dt,

случае

R( sin x, cos x) R(sin x,cos x)

делают замену tg x t ,

при ко-

торой

x arctgt ,

,sin x

cos x

или

1 t 2

замену ctg x t . Проиллюстрируем сказанное примерами.

Пример 4. Вычислить интеграл cos4 x sin 3 x dx.

Делаем

замену

cos x t .

Тогда

cos4

xsin 3 x dx t 4 (1 t 2 )dt

t 7

cos7 x

cos5 x

Пример 5. Вычислить интеграл

cos3 x

dx .

sin 4 x

Делая замену sin x t , получаем

cos3 x

(1 t 2 )dt

sin 4 x

t 4

t 2

3t3

3sin 3 x

sin x

Пример 6. Найти интеграл

dx .

sin 4 x

Делаем замену tgx t. Подставляя, получаем

(1 t 2 )2 dt

(1 t 2 )dt

sin 4

t 4 (1 t 2 )

t 4

tdt4 tdt2 31t3 1t C 13 ctg3 x ctgx C.

Заметим, что в данном примере лучше было сделать замену ctgx t , так как эта подстановка быстрее приводит к цели. Дей-

ствительно,

тогда

,sin x

, cos x

t 2

1 t 2

(1 t 2 )2 dt

поэтому

(1 t 2 )dt

t C

sin 4

(1 t 2 )

t C

ctg3 x ctgx C .

Пример 7. Вычислить интеграл cos3 xsin 8 xdx.

Делаем

замену

sin x t . Тогда

cos3 xsin 8 xdx

t8 (1 t 2 )dt

t11

sin 9 x

sin11 x

Пример 8. Вычислить интеграл

cos3 x

dx .

1 sin 2 x

Делая замену sin x t , получаем

cos3 x

(1 t 2 )dt

2 (t 2 1)

1 sin 2 x

1 t 2

2arctgt t C 2arctgsin x sin x C .

Пример 9. Найти интеграл

dx .

cos6 x

Делаем замену tgx t. Подставляя, получаем

(1 t 2 )3 dt

t 2 )2 dt

cos6 x

(1 t 2 )

dt 2t 2dt t 4dt t

2t3

2tg3 x

tg5 x

tgx

Для

интегрирования

рациональных

выражений

вида

применяют замену x a sin t или x a cost

, вы-

R x,

ражений вида

R x,

- подстановку

или

cos t

, а для интегрирования выражений вида

R x,

sin t

применяют замену x a tgt

или

x actgt . Можно в этих слу-

чаях пользоваться также заменами с гиперболическими функциями.

Пример	10. Для	вычисления	интеграла		dx

				x2
						4 x2
						4 x2
воспользуемся	заменой	x 2sin t .	Тогда dx 2costdt,
		45

4 x2 4 4sin 2 t 2 cost , и исходный интеграл равен инте-

гралу

2costdt

Тогда

4sin 2 t 2

cost

2cost dt

ctgt

Делая обратную замену

4sin 2 t 2cost

4sin 2 t

t arcsin

получаем

1 ctg(arcsin

) C

. После

4 x2

преобразований получаем

C .

2 4

Пример 11.

Для вычисления интеграла

вос-

1 x2

пользуемся

заменой

x tgt .

Тогда

cos2 t

1 x2

1 tg

исходный интеграл равен интегра-

cost

лу

costdt

Тогда

costdt

d (sin t)

Делая обрат-

sin 2 t

sin t

ную

замену

t arctgx ,

получаем

C . После преобразований по-

sin( arctg x)

1 x2

лучаем

1 x2

C .

1 x2

2.3. Задача интегрирования в конечном виде

В этой главе мы научились находить первообразные, а следовательно, и неопределённые интегралы для некоторых типов функций. В связи с этим совершенно естественным является вопрос о классе функций, для каждой из которых существует первообразная. Ответ на него даёт следующая теорема.

Теорема. Для любой непрерывной функции существует первообразная.

Обобщение понятия первообразной на функции, имеющие конечное число точек разрыва, даётся следующим образом.

Определение. Функция F(x) называется первообразной для функции f (x) (дифференциала f (x)dx ) на отрезке [a,b] , если F(x) дифференцируема на [a,b] , за исключением конечного числа точек, и F (x) f (x) во всех точках существования производной функции F(x) .

Справедлива следующая теорема.

Теорема. Для любой функции, имеющей конечное число точек разрыва 1-го рода, существует первообразная, дифференцируемая во всех точках непрерывности подынтегральной функции.

Доказательство этих результатов, а также решение задачи восстановления первообразной будут приведены в п. 2.2.

Как известно, элементарными функциями называют степенную, показательную, логарифмическую, тригонометрические и им обратные функции, а также полученные из перечисленных с помощью конечного числа их суперпозиций и конечного числа операций сложения, умножения, вычитания, деления и извлечения корня. При изучении производных мы видели, что производная элементарной функции снова есть элементарная функция. Для первообразной это не так. Не для каждой элементарной функции первообразная есть элементарная функция. Это даёт возможность введения новых, неэлементарных функций, с помощью операции интегрирования. Интегралы от функций, для которых первообразная не является элементарной функцией, называются неберущимися. Наиболее известными неэлемен-

тарными функциями являются e x2 dx ,				cos x2dx, sin x2dx,
	sin x	dx six C - интегральный синус,				cos x	dx cix C -

	x					x
интегральный косинус, lix C			dx	e y	dy - интегральный

			ln x	y

логарифм.

2.4. Замена переменных в определённом инте-

грале

Иногда возникает необходимость перейти в интеграле к новой переменной. Имеет место следующий результат.

Теорема 2.7. Пусть f (x) интегрируема на отрезке [a,b] и : [ , ] [a,b] - дифференцируемое биективное (взаимно однозначное) отображение, такое, что ( ) a; ( ) b . Тогда

b

f (x)dx f ( (t)) (t)dt .
a
	Доказательство.		Докажем теорему в предположении,
что функция			интегрируема на отрезке [ , ] .Это
что функция		f ( (t)) (t)	интегрируема на отрезке [ , ] .Это
выполнено, например, когда функции				f (x) и (t) имеют ко-
нечное	число точек		разрыва	первого рода (кусоч-
но непрерывны), так как			в этом случае функция f ( (t)) (t)

также кусочно непрерывна и, по следствию из теоремы 2.3, интегрируема. Разобьём отрезок [ , ] на части точками

t0 , t1, ... , tn . Этому разбиению отрезка [ , ] соответствует разбиение отрезка [a,b] точками xi (ti ) . Так как (t) дифференцируема, то, по теореме Лагранжа о конечных приращениях [3] , xi xi 1 xi ( i ) ti , где i [ti ,ti 1 ] - некоторая точка. Положим i ( i ) [xi , xi 1 ]. Составим интегральную сумму

n 1	n 1
f ( i ) xi	f ( ( i )) ( i ) ti .
i 0	i 0
В левой части этого равенства стоит интегральная сумма
b
для интеграла f (x)dx , а	справа - для интеграла
a

f ( (t)) (t)dt . Так как оба интеграла существуют, то, переходя

в этом равенстве к пределу по всевозможным разбиениям, получаем справедливость утверждения теоремы.

Примеры

																	4				xdx
1. Вычислить интеграл																					xdx						.		Положим x t 2 . Тогда
1. Вычислить интеграл																											.		Положим x t 2 . Тогда
																		1						x
																	0
0, 2 ,				dx 2tdt							и поэтому исходный интеграл равен
2		2t3dt						2		((t3 1) 1)dt													2				((t 1)(t 2 t 1) 1)dt
		2t3dt				2				((t3 1) 1)dt												2					((t 1)(t 2 t 1) 1)dt
0		1 t						0						1 t									0									1 t
0								0															0
2													2		dt							3						t	2					2
																																		2

			2
2 (t			2			1)dt 2														t
					t													2												t ln(1 t)
					t										1 t			2												t ln(1 t)
0													0		1 t					3						2								0
							8			4																			16
					2							2 (ln 3 ln 1)																				2ln 3.
					2							2 (ln 3 ln 1)																				2ln 3.
							3			2																			3
																	8						dx
2. Вычислить интеграл																							dx								. Положим			x 1 t		2	.
																			2
																			2						x 1
																	3
Тогда 2, 3,								dx 2tdt и поэтому
8					dx							3		tdt				3			t 2								2			3	3		dt
					dx				2					tdt		2					t 2								2	dt 2 dt 4					dt
									2							2														dt 2 dt 4
3	2		x 1									2	t 2					2				t 2										2	2		t 2
2t					3 4 ln(t						2)			3	2(3 2) 4(ln 5 ln 4) 2 4 ln 1,25.
2t					3 4 ln(t						2)			3	2(3 2) 4(ln 5 ln 4) 2 4 ln 1,25.
					2									2
					2									2

2.5. Приближённое вычисление определённого интеграла

Если первообразная является неэлементарной функцией или находится достаточно сложно, то использование формулы Ньютона-Лейбница для вычисления определённого интеграла затруднено. В этом случае определённый интеграл вычисляют приближённо, чаще всего численно. Получением некоторых формул для численного вычисления интеграла мы и займёмся.

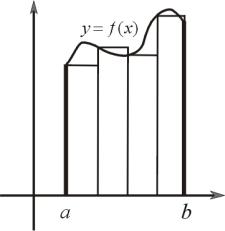
Пусть непрерывная функция f (x) задана на отрезке

[a,b] . Так как интеграл f (x)dx существует, то разобьём отре-

f (

зок [a,b] на n

частей точ-

ками xi

a ih,i 0,1,...,n ,

где h

b a

Положив в

интегральной

сумме

n 1

f ( i ) xi

последова-

i 0

тельно

i xi

i xi 1

xi xi 1

получаем

результате

формулы

для

приближённого

вычисле-

ния интеграла

n 1

b a

n 1

f (x)dx

f (xi ) xi

f (xi ) ,

i 0

n 1

b a

n 1

x)dx f (xi 1 ) xi

f (xi 1 )

f (xi ) ,

i 0

i 1

n 1

x x

b a n 1

x x

f (x)dx f

i 1

i 0

называемые формулами прямоугольников.

Называются они так потому, что криволинейная трапеция, ограниченная линиями y 0, x xi , x xi 1, y f (x) , заменяется в первом случае прямоугольником, ограниченным линиями y 0, x xi , x xi 1, y f (xi ) , во втором случае прямоугольником, ограниченным линиями y 0, x xi , x xi 1,

<<< < Предыдущая 1 2 3 45 / 205 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023984.92 Кб12Математика. Математический анализ.pdf
#
05.02.20232 Mб5Математика.-1.pdf
#
05.02.20232.61 Mб4Математика.-2.pdf
#
05.02.20232.05 Mб3Математика.-3.pdf
#
05.02.20232.49 Mб3Математика.-4.pdf
#
05.02.20233.03 Mб3Математика.-5.pdf
#
05.02.20232.78 Mб3Математика.-6.pdf
#
05.02.20232.74 Mб5Математика.-7.pdf
#
05.02.20233.16 Mб4Математика..pdf
#
05.02.2023584.83 Кб48Математическая логика и теория алгоритмов.-1.pdf
#
05.02.2023886.2 Кб6Математическая логика и теория алгоритмов.-2.pdf