
Математика.-2
.pdf
Пример |
y kx b |
Ax By C 0 |
|
x x0 kt |
(прямая) |
|
|
|
|
|
|
|
|
y y0 mt |
Поверхности |
z f (x, y) |
F (x, y, z) 0 |
|
x x(u, v) |
|
|
|
|
|
|
|
|
|
y y(u, v) |
|
|
|
|
|
|
|
|
|
z z(u, v) |
Параметрический: x x(u, v), y y(u, v), z z(u, v) |
(в этом случае |
|||
обязательно будет два параметра). Например, 2 параметра на сфере: широта и долгота.
§2. Пределы.
Последовательность.
Множество действительных чисел, пронумерованных с помощью натуральных чисел: {a1 , a2 , a3 ,..., an ,...} называется числовой
последовательностью. Еѐ можно определить также и как функцию f : N R . Графиком в этом случае будет не кривая, а дискретный набор точек.
Например, 1, |
1 |
, |
1 |
, |
1 |
,..., |
1 |
,... |
- последовательность. |
|
|
|
|
||||||
|
2 |
|
3 |
|
4 |
|
n |
|
|
Арифметическая и геометрическая прогрессии тоже частный случай последовательности.
Пример: |
|
1 |
|
1 |
|
1 |
|
1 |
|
геометрическая прогрессия |
1, |
|
, |
|
, |
|
,..., |
|
,... |
||
|
|
|
2n |
|||||||
|
|
2 |
|
4 |
|
8 |
|
|
|
В рассмотренных примерах видно, что при возрастании номера элемент убывает к 0. Однако при этом само число 0 не достигается ни при каком номере. То есть, числа 0 в этой последовательности нет. Однако, все элементы уменьшаются и приближаются к 0. В связи с этим возникает определение предела последовательности:
91

Определение. Число A называется пределом последовательности {an } , если: 0 n0 N , такое, что n n0 выполняется:
A an .
(для любого числа эпсилон больше нуля, существует такой номер элемента последовательности, что для всех последующих номеров отклонение элементов от числа А меньше, чем эпсилон). В этом случае говорится, что последовательность стремится к числу А.
Обозначение предела: A lim an . (lim это от английского слова limit
n
которое хорошо известно и в русском языке - лимиты потребления света, воды и т.д. ).
Если рассмотреть полосу от A до A по высоте, то начиная с какого-то номера, все последующие точки будут попадать в эту полосу:
Чем меньше число (погрешность меньше) тем больший номер требуется .
Пример. lim 1 0 . По определению: если например требуемая
n n
точность 0,01 то n0 100 , n n0 выполняется: разность элемента и 0 менее 1/100, то есть 1/101 затем 1/102 и т.д.
* Для того, чтобы лучше понять, что такое предел, представьте следующее. Машина приближается к городу. Для любого заранее заданного расстояния (например = 10 км.) существует такой момент времени t0 , что в последующие моменты времени t t0 расстояние
будет меньше, чем . Это как раз и означает «стремится к 0», то есть расстояние уменьшается к 0. Если задать = 5 км. то это достигается в более поздний момент времени, а если = 1 км. то ещѐ позже.
92

Предел может и не существовать. Для последовательности {1,0,1,0,....}, например, предел не существует. Здесь не происходит
стабилизация значений, то есть их колебания по высоте всегда 1. После каждого номера, найдѐтся последующий элемент, который удаляется на расстояние 1 от предыдущего, то есть эти колебания не могут быть меньше заранее заданного малого числа .
Рассмотрим последовательность |
|
1 |
|
2 |
|
3 |
|
4 |
|
n |
|
|
|
|
, |
|
, |
|
, |
|
..., |
|
|
,... |
|
|
|
|
|
n 1 |
||||||||
|
|
2 |
|
3 |
|
4 |
|
5 |
|
|
||
Вычислим предел. lim |
|
n |
|
= lim |
|
|
n / n |
|
= lim |
|
|
|
|
1 |
|
|
|
. Второе |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
n n |
1 |
n (n 1) / n |
|
|
n |
1 |
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||
слагаемое в знаменателе стремится к 0. В итоге, |
|
|
|
1 |
|
|
1, |
lim |
|
n |
=1. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
n n |
|
||||||||||
Таким же методом можно сокращать старшие степени и в других |
|
||||||||||||||||||||||||||||||||||||||||||
случаях, для произвольных степеней. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
an2 |
n 1 |
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim |
= |
lim |
n |
n2 |
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n bn2 |
|
n |
|
|
1 2 |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
n |
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
при s k |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
s |
... |
|
|
|
|
|
b |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В общем случае, когда степени разные: lim |
|
|
|
= 0 |
при s k . |
||||||||||||||||||||||||||||||||||||||
|
|
|
... |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n bnk |
|
|
|
|
при s k |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теорема 1. Пусть дано 3 последовательности, причѐм для любого |
|
||||||||||||||||||||||||||||||||||||||||||
номера n: un vn |
wn . |
Если |
|
lim un |
A и lim wn |
|
|
A то существует |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim vn и тоже равен A .
n
Доказательство. Так как для первой и третьей последовательности
предел равен |
А, |
то |
числа un , wn (начиная с какого-то |
номера) |
отклоняются |
от |
A |
не больше чем на величину , |
то есть |
принадлежат интервалу ( A , A ) . Но число vn находится между ними, тогда оно тоже принадлежит ( A , A ) . Тогда по
93

определению, для средней последовательности тоже существует предел.
Теорема 2. Если последовательность монотонно возрастает (убывает) и ограничена сверху (снизу), то она имеет конечный предел.
Примеры нарушения одного из этих двух условий. {1,2,3,...,n,...} не ограничена, предел .
{1,0,1,0,....} не монотонна. Пределом не может быть ни одно из чисел 0
или 1. Здесь после любого элемента, среди последующих есть какойлибо, удалѐнный от данного на расстояние 1, то есть в определении предела было бы не «для любого », а только для >1. Колебания по высоте не уменьшаются, все последующие элементы не впишутся в узкую полосу ширины 2 .
Предел функции при x .
Число A называется пределом функции f (x) , при x если:
0 |
M R , так, что x M выполняется: |
|
f (x) A |
|
. |
|
|
||||
|
|
|
|
|
|
Объяснение: для любой заранее заданной погрешности существует такая константа М, что правее неѐ график отклоняется от ординаты А не более, чем на .
Аналогично определяется предел при x для левой полуоси.
94
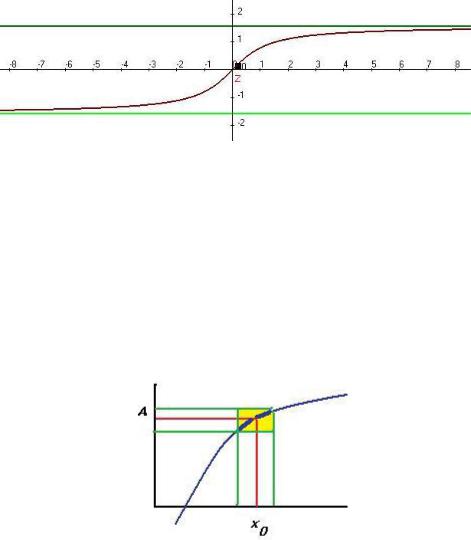
Пример. |
f (x) arctg(x) . Два различных предела при и |
. |
||||
lim arctg(x) |
. |
Предел на правой полуоси равен |
|
, но при этом |
||
x |
|
2 |
|
2 |
|
|
ни в одной точке x R функция не принимает это значение.
Предел функции в точке (при x x0 ).
Определение. Число A называется пределом функции f (x) в
точке x0 , если: 0 0 , такое, что при 0 |
|
x x0 |
|
|
||||
|
|
|||||||
выполняется: |
|
A f (x) |
|
. |
|
|
||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
(для любого числа эпсилон больше нуля, существует такое число дельта, так что если модуль разности x x0 меньше дельта, то модуль разности f (x) A меньше, чем эпсилон).
Обозначение A lim f (x) .
x x0
В случае существования предела, получается, что задавая погрешность можно найти такой интервал в области определения, что отклонение значений от А будет меньше чем . Фактически,
95

часть графика впишется в некоторый прямоугольник, при уменьшении одной стороны будет уменьшаться и вторая.
Существует пример функции, не имеющей предела в нуле.
|
1 |
|
f (x) sin |
|
. Здесь при приближении к 0 бесконечное число |
|
||
x |
|
|
колебаний, то есть, уменьшая область определения, например интервал ( , ) , никак не удастся получить уменьшение области
значений функции над этим интервалом, размах колебаний всѐ равно останется от -1 до 1. При подходе абсциссы к 0, функция здесь должна пройти бесконечное число колебаний амплитуды 2 (от -1 до
1).
Но даже для «обычных» функций, не испытывающих бесконечное количество колебаний, не всегда существует значение функции в точке. Бывает так, что формально еѐ вычислить нельзя.
Например, для функции |
x2 |
9 |
значение в точке |
x0 =3 не существует. |
|
x |
3 |
||||
|
|
|
При вычислении на калькуляторе поочерѐдно числителя и
знаменателя, получили бы |
0 |
и |
калькуляторы, компьютеры выдали |
|
0 |
||||
|
|
|
||
бы сообщение об ошибке. |
|
Но |
ведь в соседних точках значение |
96

функции есть, график функции подходит к некоторой точке в плоскости. Так вот, еѐ ордината и равна этому пределу.
Пример. Вычислить предел lim |
x 2 |
9 |
. |
|
x |
3 |
|||
x 3 |
|
В точке 3 значение функции не существует, однако во всех соседних точках существует, и можно узнать, к какой ординате стремится график при x 3 . Разложим на множители:
lim |
x 2 |
9 |
= lim |
(x 3)(x 3) |
= lim |
(x 3) |
= 6. |
|
x |
3 |
x 3 |
1 |
|||||
x 3 |
x 3 |
x 3 |
|
Тот множитель, который отвечал за стремление к 0 в числителе и знаменателе, сокращѐн, поэтому далее удалось просто подставить 3 и получить ответ.
ЛЕКЦИЯ № 10. 07. 11. 2017
Вычислим предел одной и той же функции при x 0 и при x .
lim |
x 2 |
x |
= lim |
x(x 1) |
= lim |
x 1 |
= |
1 |
. |
x 0 x 2 2x |
x 0 |
x(x 2) |
x 0 |
x 2 |
|
2 |
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
x 2 x |
|
|
1 |
|
|
|
|
|
|
|
||
lim |
|
= lim |
x |
|
= 1. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
x x 2 2x |
x |
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
x |
|
|
|
|
|
||||
Как видим, |
методы разные: если неопределѐнность |
типа |
0 |
, то |
|||||||||
0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
выделяем множители, |
|
для того, чтобы сократить те |
множители, |
||||||||||
которые стремятся к 0. Если неопределѐнность , то корни искать не нужно, а нужно сократить на степенную функцию старшей степени.
Метод Лопиталя для неопределѐнностей 00 . Несмотря на то, что тема
«производные» подробно будет позже, и доказательство этого метода будет дано в той теме, производные для некоторых элементарных функций известны из школы, и можно этим пользоваться при вычислении пределов.
97

Если f (x) 0 , |
g(x) 0 при x x |
|
и lim |
f (x) |
A , |
|
||||||||
0 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
x x0 |
g (x) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
то lim |
f (x) |
A . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x x0 |
g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. lim |
x 2 |
x |
= lim |
(x2 x) |
= lim |
2x 1 |
= |
1 |
. |
|||||
|
|
|
|
|
|
|
|
|||||||
|
x 0 x 2 2x |
x 0 (x2 2x) |
x 0 |
2x 2 |
|
2 |
|
|||||||
Этот метод можно применять и в 2 или более шагов, если после 1-го дифференцирования остаѐтся неопределѐнность 0 0 .
0 .
|
|
|
|
1 |
|
|
|
|
ln(1 x) |
|
|
|
|
|
|
|
|
|
|
|
|||
Вычислим этим же способом: lim |
= lim |
1 |
x |
= 1. |
|||
x |
|
|
1 |
|
|||
x 0 |
x 0 |
|
|
|
|
||
График ln(1+x) это ln(x) сдвинутый влево на 1, касательная проходит ровно под углом 45 градусов, то есть совпадает с функцияей y = x. Если рассмотреть при большом увеличении, они почти неотличимы.
Ещѐ пример. lim |
sin x |
lim |
(sin x) |
lim |
cos x |
1. |
|||
x |
(x) |
1 |
|||||||
x 0 |
x 0 |
x 0 |
|
||||||
1-й замечательный предел. |
lim |
sin x |
1 . |
|
|||||
|
|
||||||||
|
|
|
x 0 |
x |
|
|
|||
Доказательство 1-го замечательного предела из геометрических соображений.
Рассмотрим единичную окружность, и какой-либо угол. Длина дуги AB равна - это по определению радианной меры угла. Так как ОА это радиус, а мы взяли единичную окружность, то
98

|
| AC | |
|
| AC | |
tg . |
|
|||||
|
|
|
|
|
||||||
|
| OA | |
1 |
|
|
|
|
|
|||
Так как ОВ это тоже радиус, то |
|
| BD | |
|
| BD | |
sin . |
|||||
|
| OB | |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|||
Но длина дуги на чертеже больше, чем отрезок BD, и меньше, чем AC. | BD | | AC | , то есть sin tg .
Совпадают они именно при 0 .
Кстати, графики трѐх функций именно так и расположены: у них общая касательная, тангенс выше, синус ниже, чем биссектриса.
Неравенства sin tg перепишем в виде: sin |
sin |
. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Теперь разделим всѐ на синус. 1 |
|
|
|
. Рассмотрим обратные |
||||||||||||||||||
sin |
cos |
|||||||||||||||||||||
величины ко всем этим, пользуясь тем, что из a b следует |
1 |
|
|
1 |
. |
|
||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|||
Получится |
cos |
sin |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применим |
свойство, |
которое |
доказывали |
когда-то |
ранее: |
|
если |
|||||||||||||||
u v w и две крайние из 3 |
величин стремятся к А, |
то и средняя |
||||||||||||||||||||
имеет предел и стремится к А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Учитывая, |
что |
lim cos 1, а |
константа справа и так равна |
1, |
то |
|||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
sin |
1 . Если |
обозначение |
угла |
сменить, обозначить x, |
|
то |
и |
||||||||||||||
|
|
|||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получается lim |
sin x |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следствия из 1-го замечательного предела:
99
lim |
tgx |
1, lim |
arcsin x |
1, |
lim |
arctgx |
1 , |
lim |
sin a(x) |
1. |
|||||
|
|
|
|
a(x) |
|||||||||||
x 0 x |
x 0 |
x |
x 0 |
|
x |
|
a( x) 0 |
|
|||||||
Пример. lim |
sin 3x |
lim |
sin(3x) |
|
3 1 3 3 . |
|
|
||||||||
|
|
|
|
||||||||||||
|
|
x 0 |
x |
x 0 (3x) |
|
|
|
|
|
|
|||||
Более подробно: мы могли бы заменить t 3x , и учесть, что при x 0 будет и t 0 .
Пример. Найти предел lim |
sin(x2 1) |
. |
|
x 1 |
|||
x 1 |
|
Решение. Надо получить в знаменателе такое же выражение, как под знаком sin.
lim |
sin(x2 1) |
= lim |
sin(x 2 1) |
|
(x 1) |
= |
lim |
sin(x2 1) |
lim(x 1) = 2. |
||||||||
x 1 |
x 1 |
x 1 |
(x 1)( x |
1) |
|
|
|
x 1 |
|
(x2 1) |
|
|
x 1 |
|
|||
Здесь можно в процессе решения переобозначить (x) x2 1, |
|||||||||||||||||
причѐм (x) 0 при x 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
1 x |
|
|||
2-й замечательный предел. |
|
lim 1 |
|
|
|
e |
lim 1 |
|
|
|
|
e |
|||||
|
|
|
|||||||||||||||
|
|
|
|
|
n |
|
n |
|
|
n |
|
|
x |
|
|||
Обратите внимание, что этот предел вовсе не 1, как могло бы показаться. Ведь в степень всегда возводится не 1, а число, большее, чем 1. Оно уменьшается, но оно ни при каком n не равно 1. Здесь 2 процесса: одновременно уменьшается основание до единицы, и при этом увеличивается степень. Всѐ зависит от соотношения скоростей этих процессов.
Если, к примеру, есть 2 процесса: растворение краски и замораживание ѐмкости с водой, то существенно отличается результат, если выполнить 1-й или 2-й процесс раньше. Если сначала заморозить воду, то уже ничего не растворится, а если сначала растворить, то будет равномерная смесь. Если замораживать одновременно с растворением, то будет другой результат, краска растворится не равномерно. Короче говоря, мы не имеем права
|
|
1 |
n |
|
считать, что сначала уменьшили основание в выражении 1 |
|
|
и |
|
|
||||
|
|
n |
|
|
только потом стали увеличивать степень, здесь оба процесса идут
100
