Математика.-2

Матрица оператора относительно нового базиса задаѐтся формулой

B C 1 AC , где A, B - матрицы оператора в старом и новом базисах, С - матрица перехода к новому базису.

Идея доказательства: Aci это образы ci , т.е. векторов нового базиса.

Чтобы выразить их в том же новом базисе, нужно решить систему уравнений, где основная матрица это матрица перехода С . А решение такой системы равносильно умножению на обратную матрицу.

Теорема 5. Если базис состоит из собственных векторов, то матрица оператора в этом базисе диагональна.

Доказательство.

Le1 1e1 1e1 0e2 0e3 ...0en , то есть 1-й столбец в матрице оператора это такие числа: ( 1 ,0,0,..., 0) .

Аналогично Le2 2 e2 0e1 2 e2 0e3 ...0en , то есть 2-й столбец

(0, 2 ,0,..., 0) . И т.д.

выполняется свойство (Ax,y) = (x,Ay).

Доказательство. Рассмотрим это равенство для базисных векторов: ( Aei , e j ) (ei , Ae j ) . Если оно выполняется для любой пары базисных

векторов, то есть для любых индексов i, j .

51

Aei , как показано раньше, это i-й столбец матрицы линейного оператора. Если скалярно умножить его на e j , то есть на тот вектор,

где все координаты 0 и только на месте j единица, - получим j - й элемент из i - го столбца, это a ji в матрице.

Аналогично, (ei , Ae j ) это i - й элемент из j - го столбца, то есть aij . Таким образом, ( Aei , e j ) (ei , Ae j ) эквивалентно тому, что aij = a ji

для всех индексов i, j.

Определение. Если для линейного оператора L , для любой пары векторов x, y верно (Lx, y) (x, Ly) , то L называется симметрическим оператором.

Собственные числа разные, поэтому первый множитель не равен 0, тогда (x, y) 0 . Скалярное произведение 0, векторы ортогональны.

Следствие. Для линейного оператора, матрица которого симметрична, существует ортогональный базис, состоящий из собственных векторов.

52

ЛЕКЦИЯ № 6. 10. 10. 2017 § 3. Квадратичные формы.

Рассмотрим подробнее скалярное произведение типа (x, Ay) , где А - матрица некоторого линейного оператора. Произведение квадратной матрицы на столбец y это вектор-столбец, если затем его скалярно умножить на вектор x , получится число. Таким образом, (x, Ay) это

некоторая скалярная функция от 2 векторов. Она линейна по каждому аргументу: если на 1 или 2 месте сумма векторов, то результат тоже

a11 x1 y1 a12 x1 y2 a21 x2 y1 a22 x2 y2 .

Фактически, это - обобщѐнное скалярное произведение. Обычное скалярное произведение - частный случай билинейной формы. Его можно задать таким же способом, с помощью единичной матрицы Е:

Теперь рассмотрим такой случай. Пусть билинейная форма

число, квадратичной формой. Квадратичная форма задаѐтся через скалярное произведение так: Q(x) (x, Ax) .

53

Очевидно, x1 x2 x2 x1 , то есть эта группа из двух слагаемых a12 x1 x2 и

сделать симметричной, перераспределить эквивалентные элементы с сохранением их суммы. Эта же самая квадратичная форма может быть

Таким образом, квадратичную форму всегда можно задать симметричной матрицей. Вспомним теорему 7 из прошлого §. Если матрица симметрична, то собственные векторы ортогональны.

Если матрица диагональна, то:

т.е. квадратичная форма не содержит попарных произведений, а содержит только квадраты координат.

А теперь вспомним также теорему 5 из прошлого §. Если в качестве нового базиса взять n собственных векторов, то матрица оператора в новом базисе будет диагональной. Из всего сказанного следует, что квадратичную форму всегда можно привести к виду, не содержащему попарные произведения, а содержащему лишь квадраты, называется к «главным осям» (главные оси это направления, соответствующие собственным векторам). Приведение к главным осям основано на поиске собственных чисел и векторов, примеры на эту тему решим подробно на практике.

54

Глава 4. Аналитическая геометрия.

§1. Прямая на плоскости и плоскость в пространстве

Известно из школы такое уравнение прямой: y kx b . Однако оно не позволяет задавать вертикальные прямые. Существует более

Аналогично, для плоскости в пространстве. Эта ситуация похожа на прямую в плоскости: до всего пространства не хватает 1 размерности, плоскость это 2-мерное множество в 3-мерном пространстве. Нормаль однозначно определяет плоскость в пространстве. Явное уравнение плоскости: z kx my c . Но таким путѐм невозможно задать

никакую вертикальную плоскость, то есть явное уравнение применимо не ко всем ситуациям. Общее, или неявное уравнение плоскости: Ax By Cz D 0 .

Пункт 1. Вывод уравнений по точке и перпендикуляру. Прямая в R2.

Допустим, дана точка M 0 с координатами (x0 , y0 ) и перпендикуляр (синоним: «нормаль») к прямой, вектор n . Если произвольную точку

55

Тогда скалярное произведение, пары векторов (x x0 , y y0 , z z0 ) и

( A, B,C) равно 0. Итак, A(x x0 ) B( y y0 ) C(z z0 ) 0 .

Раскроем скобки: Ax By Cz ( Ax0 By0 Cz0 ) 0 . Обозначим константу Ax0 By0 Cz0 D . Тогда получается

Ax By Cz D 0 . Обратите внимание, что координаты нормали оказались именно коэффициентами при x,y,z.

Пример. Найти уравнение плоскости, проходящей через точку (1,1,1) перпендикулярно вектору (1,2,3).

Решение. Вектор (x 1, y 1, z 1) ортогонален вектору (1,2,3).

Тогда 1(x 1) 2( y 1) 3(z 1) 0 следовательно, x 2 y 3z 6 0 .

Замечание. Длина нормали не влияет на уравнение. Если бы изначально было дано, что нормаль (2,4,6) то получили бы:

2x 4y 6z 12 0 , но это уравнение задаѐт ту же самую плоскость. Достаточно вынести 2 за скобку, и сократить на 2, получили бы

2(x 2 y 3z 6) 2 0 0 .

произвольную точку M (x, y) на прямой. В данном пункте M 0 M не

«каноническое уравнение прямой». Можно свести к общему виду,

умножив крайние и средние члены пропорции: m(x x0 ) k( y y0 ) , сводится к mx ky C 0 .

Заметим, что здесь A m, B k . То есть, можно было бы и сразу от направляющего перейти к нормали, для этого поменять

57

местами координаты вектора, и у одной координаты сменть знак. А потом действовать как в прошлом пункте.

Пример. Найти уравнение прямой, проходящей через точку (1,2) параллельно вектору (3,4).

Замечание. Построение уравнения прямой по двум точкам

сводится к этому же методу, так как вектор, проведѐнный между этими точками, как раз и есть направляющий к прямой.

Плоскость в R3. Для плоскости, необходимо 2 направляющих. Пусть даны точка M 0 (x0 , y0 , z0 ) и 2 направляющих вектора l1 , l2 ими

однозначно порождается некоторый параллелограмм, а следовательно и плоскость. Одного направляющего вектора недостаточно, ведь тогда плоскость может вращаться вокруг него, то есть плоскость не будет однозначно фиксирована. Обозначим координаты направляющих,

например, так: l1 ( p1 , q1 , r1 ) и l2 ( p2 , q2 , r2 ) .

Первый способ. Можно найти нормаль к плоскости как векторное произведение 2 направляющих векторов n [l1 ,l2 ] и далее искать

уравнение плоскости по точке и нормали, методом, рассмотренным в пункте 1. Но это будет решение в 2 шага.

Однако можно также получить уравнение плоскости сразу, без вычисления векторного произведения:

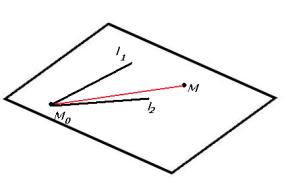
Второй способ. Возьмѐм произвольную точку M (x, y, z) . Если она

образует линейно-зависимую систему (ЛЗС), то есть эти векторы не образуют параллелепипед, а лежат в одной плоскости. Тогда смешанное произведение 0, то есть определитель, составленный из них, равен 0:

58

Пункт 3. Расстояние от точки до прямой (плоскости).

(чертѐж с доски)

1)длина проекции r это катет, a гипотенуза треугольника, тогда получается, что ar cos .

2)известно, что (a,b) ab cos .

Кратчайшее расстояние, то есть длину перпендикуляра, проведѐнного от точки к прямой, обозначим d. Нам не известно, где основание перпендикуляра, более того, его и не нужно искать. Возьмѐм произвольную точку M 0 на прямой. Это можно сделать так: присвоим

x=0 и вычислим y, либо наоборот, y=0 и вычислить x. Короче, найти какую-нибудь точку на прямой можно элементарно. Далее, соединим M 0 и M1 . Вектор M 0 M1 не перпендикулярен прямой, однако его

проекция на нормаль это и есть d.

60