
Исследование операций и методы оптимизации
..pdf
|
|
|
|
|
∆z = β ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y ± ∆y = f (x ± ∆x(α) z ± ∆z(β)) |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
α + β =1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
∆x |
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где ∆ , ∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
– приращение аргументов; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соот- |
|||
|
α β – коэффициенты относительной важности приращений ∆ , ∆ |
|||||||||||||||||||||||||
ветственно; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
– исходное значение и приращение результирующей функции. |
|
|
||||||||||||||||||||||||
|
|
∆ |
|
|
||||||||||||||||||||||
|
Знак «п юс» или «минус» говорит о том, будет ли зна ение аргумента |
|||||||||||||||||||||||||
уменьшатся |
или увеличиваться для решения поставленной |
задачи. |
|
|
|
|
||||||||||||||||||||
|
Определение цены |
количества товара может быть выполнено тремя |
||||||||||||||||||||||||
способами |
|
в зависимости |
от соотношения величин прироста аргументов |
|||||||||||||||||||||||
(табл. 2.9). Так, если нужно увеличить значение выручки, то это может быть |
||||||||||||||||||||||||||
достигнуто следующими |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|||||||
1) |
увеличение ценыспособами:количества |
|
|
|
|
( − ). В этом случае, |
||||||||||||||||||||
2) |
увеличение цены ( |
+ ) |
и уменьшение количества |
|||||||||||||||||||||||
|
|
|
|
|
|
|
( |
|
) |
|
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
чтобы произошло увелич ние выручки, увеличение цены должно быть |
||||||||||||||||||||||||
|
|
выполнено в большей степени, чем уменьшение колич ства, поэтому |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
должен быть выше, |
|||||
|
|
коэффициент относительной важности цены |
(α) |
|
||||||||||||||||||||||
3) |
чем коэффициент относительной важности количества |
(β); |
|
|
||||||||||||||||||||||
уменьшение цены |
( − ) |
и увеличение количества |
( + ) |
. В этом случае, |
||||||||||||||||||||||
|
|
чтобы произ шло |
|
|
|
|
выручки, увелич |
|
количества долж |
|||||||||||||||||
|
|
но быть выполненоувеличениебольшей степени, чем уменьшение |
цены, поэто- |
|||||||||||||||||||||||
|
|
му коэффициент относительной важности количества |
(β) должен |
|||||||||||||||||||||||
|
|
быть выше, чем коэффициент относительной важности цены (α). |
||||||||||||||||||||||||
|
|
|
|
Таблица 2.9 – Варианты достижения цели |
|
|
|
|
|
|||||||||||||||||
|
Вид зависимости |
|
|
|
|
|
|
+ |
Прирост результата |
– |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Мультипликативная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
+ |
+ |
|
|
+ − |
|
− + |
|
|
− |
− |
|
+ |
− |
|
− |
+ |
|
|||||
|
α |
β |
|
|
|
|
|
|
|
|
α > β |
|
α < β |
|
|
|
|
|
|
α < β |
|
α > β |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Установим |
значенияβ = |
коэффициентов важности приращений аргументов |
||||
функции: α = |
|
. |
|
|
|
|
Тогда решение задачи для случая увеличения аргументов может быть по- |
||||||
лучено следующим образом: |
|
= . |
( + ∆ |
)( + ∆ ) |
||
|
|
|
|
|||
|
|
+ ∆ = |
||||
|
|
|
|
α |
∆p = |
|
|
|
∆p |
|
|
||
|
|
∆c |
β |
|
|
|
|
|
|
в уравнение и решим его: |
|
|
|
||||||||||||||||
Подставим полученное выражение |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
∆ |
= |
∆ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(c + ∆c)( p + ∆c) = |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
( |
|
∆c2 |
+ |
|
∆c − |
= |
|
|
|
|
|
|
|
|
|
|||||
|
|
+ ∆c)( |
+ |
∆c) |
= |
|
|
|
|
|
|
|
|
|
|
|||||||
Значения количества проданного товара |
|
|
цены равны: |
= |
, |
= . |
|
|||||||||||||||
Рассмотрим также решение |
детерминированной обратной задачи с адди- |
|||||||||||||||||||||
|
|
|
|
|
|
|
∆ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
||
тивной исходной функцией. |
|
|
∆ |
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
), и прибыль, направляемая |
||||||||
Прибыль, направленная на потребление |
( |
|
|
|||||||||||||||||||
на инвестиции ( ), образует общую прибыль |
( |
|
|
): |
|
, β = |
|
. Нужно |
||||||||||||||
Исходные |
данные: |
|
= |
|
|
, |
= |
= |
+ , |
|
|
|
= |
, α = |
|
|||||||
определить такие значения |
|
|
|
и |
|
|
, при которых общая прибыль будет рав- |
|||||||||||||||
на 18. Этого можно добиться двумя |
|
|
|
|
|
|
|
уменьшив значения |
|
и |
, |
|||||||||||
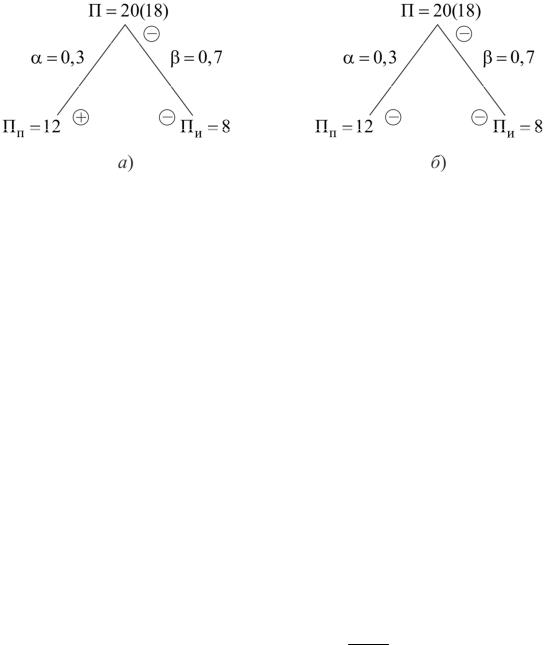
Решение для случая на рисункеспособами:2.13, |
|
|
|
|
|
|
|
|
||||||||||||||
либо увеличив |
и уменьшив |
|
|
|
(рис. 2.13, |
, б). |
|
|
|
|
||||||||||||
|
|
п |
= . |
|
|
|
|
|
|
|
|
|
− ∆ ) |
|
|
|
|
|||||
|
− ∆ = + ∆ + ( |
|
|
|
|
|
|
|
|
|||||||||||||
|
∆Пи |
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∆ |
п |
= |
|
α∆ |
|
|
∆ и |
= − |
|
∆ |
|
|
|
|
|
||||||
|
|
|
β |
|
|
α |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β − |
|
|
|
|
||
63
Рис. 2.13 – |
расчета общей |
|
|
|
|
|
|
|
|
в случае |
|
|
зменения показателей: |
|||||||
|
Деревоа) разных направлениях;прибыли) в одном направлении |
|||||||||||||||||||
Подставив значение, получим: |
|
|
0,732 |
−1 = 3,5; |
|
|
|
|
|
|||||||||||
|
|
|
∆Пи = − |
|
|
|
|
|
||||||||||||
|
|
|
∆Пп = |
|
0,3 3,5 |
|
=1,5; |
|
|
|
|
|
||||||||
|
|
|
|
|
0,7 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
8 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Пи = |
− 3 |
|
= 4,5; |
|
|
|
|
|
|
||||||||
|
|
|
П |
= |
12 |
+1,5 |
= |
13,5. |
|
|
|
|
|
|||||||
В случае на рисунке 2.13, б |
уменьшаются оба показателя, причем в боль- |
|||||||||||||||||||
шей степени уменьшение происходит |
за счет величины П |
и |
: |
|||||||||||||||||
|
П − ∆П = П |
п |
|
− ∆П |
п |
+ (П |
и |
− ∆П |
и |
); |
|
|||||||||
|
|
∆Пп |
= β . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∆Пип = α∆Пи , ∆Пи = − ∆П . |
|
|
|
|||||||||||||||
|
|
∆ |
α |
|
|
|
|
|
|
|
|
|
|
|
β +1 |
|
|
|
|
|
Подставив значение, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
∆Пи = − |
0,732+1 =1,4; |
|
|
|
|
|
|||||||||||
|
|
|
∆Пп = |
|
0,3 1,4 |
= 0,6; |
|
|
|
|
|
|||||||||
|
|
|
|
|
0,7 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
8 |
−1,4 |
|
|
|
|
|
|
|
|||||||||
|
|
|
Пи = |
= |
6,6; |
|
|
|
|
|
|
|||||||||
|
|
|
Пп |
= |
12 |
− 0,6 |
= |
11,4. |
|
|
|
|
|
|||||||

|
|
Рассмотрим другой вид целевой функции: прибыль равна выручка минус |
||||||||||||||||||||||||||
себестоимость ( |
− |
). |
|
|
|
|
в следующем: необходимо нарастить прибыль |
|||||||||||||||||||||
|
|
Целевая установка |
|
|
|
|
|
|||||||||||||||||||||
за счет повышения выручкисостоитсебестоимости, причем бол |
|
часть прироста |
||||||||||||||||||||||||||
рибыли должна произойти за счет повышения прибыли, |
ьшаям ньшая – за счет |
|||||||||||||||||||||||||||
повышения себестоимости. Такая целевая установка отражается |
следующим |
|||||||||||||||||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Представим эту задачу в виде системы уравнений: |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
+ = |
|
|
+ |
(α) − |
|
|
+ (β) |
α > β |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
∆С = |
β . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
+ ∆ |
и |
= |
|
+ ∆ |
|
− |
− ∆ |
|
|
|
|
|
|
|||||||||
|
|
Решив ее относительно ∆ |
|
∆ |
|
|
получим: |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
∆В |
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя полученное выражение в первое уравнение, получим: |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∆ = |
α |
∆ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆П |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
······················· |
|
|
|
|
|
α |
|
|
|
|
|
······················· |
||||||||||||||||
|
|
|
|
|
|
|
|
Пример 2.8 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
− |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Пусть исходные значения равны: α = |
|
|
; β = |
; |
= |
; |
= |
; |
= ; |
|||||||||||||||||
∆ |
= |
|
(рис. 2.14). Тогда: |
|
|
|
|
|
∆П |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
∆ |
= |
|
|
|
|
= |
|
,7 |
|
|
= |
|
|
|
|
|
|
||||||
|
|
|
|
|
α |
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
β |
|
|
|
,7 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
−1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
чение |
Следовательно, новое значение выручки будет равно: |
= |
+ |
= |
, зна- |
|||||||||||||||||||||||
|
|
составит |
|
|
|
= |
|
|
+ |
|
= |
|
|
, а прибыль |
будет равна |
= |
||||||||||||
= |
− |
себестоимости= , . . её увеличение равно заданному значению (∆ = |
). |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∆ |
|
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||
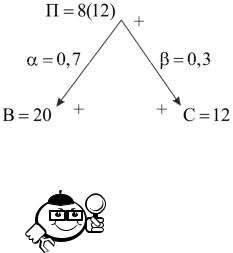
65
Рис. 2.14 – Задача |
|
|
|
|
|
|
|
себестоимости |
|
································································· |
|||||||||
······················· |
|
|
Пример 2.9 ······················· |
||||||
Рассмотрим следующий пример. Рентабельность Р рассчитывается деле |
|||||||||
нием прибыли |
П на себестоимость |
|
|
|
|
|
|
С. Необходимо увеличить рен- |
|
табельность за счет повышения прибылипродукцииснижения себестоимости, причем |
|||||||||
большая часть увеличения рентабельности должна произойти за счет повыше- |
|||||||||
ния прибыли, |
меньшая – за счет снижения себестоимости. Такая целевая |
||||||||
установка представляется следующим образом: |
|
||||||||
Составим систему уравнений: |
С− |
(β) |
|
|
|
||||
|
Р+ = |
П+ |
(α), α > β. |
|
|||||
|
Р + ∆Р |
= |
|
П |
+ ∆П |
; |
|
||
|
|
С |
|
|
|||||
|
|
|
|
|
|
− ∆С |
|
||
|
∆С = β . |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Выражаем из второго уравнения изменение прибыли: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
∆П |
α |
|
|
|
|
|
||
|
∆П = α ∆С. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
Подставляем его в первое уравнение: |
|
|
|
||||||
|
|
|
|
П + α ∆С |
|
||||
|
Р + ∆Р = |
|
β |
|
|
|
|||
|
|
|
С − ∆С ; |
||||||
|
|
|
|
|
|
|
β |
|
|
П + |
α ∆С = С Р − ∆С Р + С ∆Р − ∆С ∆Р; |
|
|
|
П + α ∆С = (Р + ∆Р)(С − ∆С); |
α ∆С |
β |
|
+ ∆С Р + ∆С ∆Р = С Р + С ∆Р − П; |
||
|
β |
|
β

|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
β |
|
|
+ + ∆ |
= + ∆ − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ = |
|
С |
Р + С ∆Р − П |
= |
( |
|
+ ∆ ) |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
α |
|
|
|
|
; |
|
|
; |
|
|
|
|
|
; ∆ |
|
|
. |
|
|
|||||||||||||||
|
Исходные значения: |
β |
+ |
; β |
|
; |
|
|
β |
+ |
+ ∆ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
α |
+ ∆ |
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Тогда изменение себестоимости составит: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
∆ = С (Р + ∆Р)− |
П = 4 |
(6 |
|
+ 4)− 24 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Изменение прибыли: |
α |
|
+ Р + ∆Р |
7 |
|
|
,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
β |
|
|
|
0,3 + 6 + 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
= |
0,3 |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, новые значения себестоимости и прибыли будут равны |
||||||||||||||||||||||||||||||||||||||
·································································− = и + = соответственно. Рентабельность составит |
|
|
= . |
||||||||||||||||||||||||||||||||||||
|
Если результирующая величина зависит от не кольких переменных, |
||||||||||||||||||||||||||||||||||||||
можно использовать процедуру свертки либо решить систему с |
|
|
+ |
|
уравнени- |
||||||||||||||||||||||||||||||||||
ями ( |
– число аргументов). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Рассмотрим случай зависимости от трех аргументов. Общие затраты |
( ) |
|||||||||||||||||||||||||||||||||||||
включают материальные затраты |
( |
), затраты на оплату труда |
( |
|
) |
затраты |
|||||||||||||||||||||||||||||||||
на аренду помещения |
( |
): |
|
|
= |
+ |
+ |
|
. Допустим, необходимо |
снизить |
уро- |
||||||||||||||||||||||||||||
вень затраты за счет снижения всех элементов. Тогда целевая установка будет |
|||||||||||||||||||||||||||||||||||||||
иметь следующий вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которая будет равна сумме двух |
||||||||||||||||||||||
|
Свернем эту формулу. Введем |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
последних затрат: Т |
|
(β)+ А |
|
|
( |
γ) = О величину,(σ) σ = β + γ |
. |
|
|
|
З |
|
= |
М |
|
(α)+ О |
|
(σ). |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
− |
= |
− |
(α) |
+ |
− (β)+ |
|
− |
( |
γ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Далее последовательно решаются две задачи |
|
|
|
двумяТогдагументами, при этом |
|||||||||||||||||||||||||||||||||||
значения коэффициентов относительной |
важности нормируются. |
|
− |
|
|
|
− |
|
|||||||||||||||||||||||||||||||
|
|
|
− |
|
|
|
|
|
− |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|||
······················· |
|
|
|
|
|
|
Пример 2.10 ······················· |
||||||||||||||||||||||||||||||||
|
Рассмотрим эту задачу для следующих |
исходных |
|
данных |
|
(рис. 2.15): |
|||||||||||||||||||||||||||||||||
α = ; β = |
; γ = |
|
|
; |
|
|
= |
|
|
|
; |
= |
; |
= |
; |
|
|
|
= |
|
; ∆ = . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
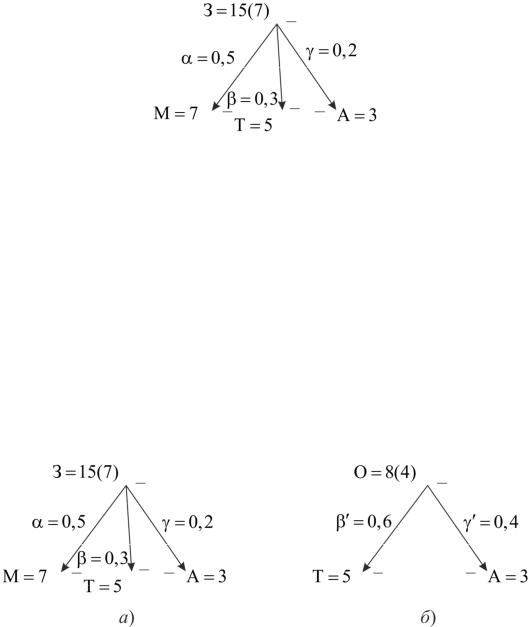
67
Тогда |
Рис. 2 |
О = Т + А = 8;аргументами |
|
||
|
|
σ = 0,3+ 0,2 = 0,5. |
а): |
||
Решаем систему (графическое представление задачи на рисунке 2.16, |
|||||
|
З − ∆З = |
М − ∆М + О − ∆О; |
|
||
|
∆М |
= α |
; |
|
|
|
|
|
|
||
|
∆М = ∆О α . |
|
|||
|
|
σ |
|
|
|
|
∆О |
|
|
||
σ
Рис. 2.16 – Представление задачи и подзадачи |
|||||||
Подставляем выражение в первое уравнение, получим: |
|||||||
∆О = |
1 |
∆З |
= |
1 |
8 |
|
= 4; |
|
+ σ |
|
+ 0,5 |
= 4. |
|||
∆М = ∆О |
σ = |
4 0,5 |
|
||||
|
|
α |
|
|
|
модель Т− (β)+ А− (γ) = О− (σ), |
|
Теперь нужно рассмотреть вторую |
|||||||
|
|
α |
|
|
|
|
|
σ = β + γ и найти значения Т и А (рис. 2.16, б). |
|
||||||
Выполним нормирование коэффициентов относительной важн сти (т. к. |
||||||||||||||||||||||||||
их сумма должна быть равна 1). Для этого разделим значение |
каждого коэффи- |
|||||||||||||||||||||||||
циента важности на сумму двух коэффициентов: |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,5 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
β + γ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
β′ = |
|
β + γ |
= |
0,5 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
β |
|
3 = |
|
|
|
|
|
||||||||||
Получим систему уравнений: |
γ |
|
|
|
|
2 = |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
γ′ = |
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||
Из этой системы: |
|
− ∆ |
= |
− ∆ |
|
+ − ∆ |
|
|
|
|
||||||||||||||||
|
∆Т |
|
|
β′. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
∆А |
|
|
γ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
∆О |
|
|
1 |
+ |
4 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1+ |
|
γ′ |
|
|
0,4 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
∆ |
= ∆ |
β′ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ = |
|
|
|
|
β′ = |
|
|
|
|
|
6 = |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
= ; |
|||||||||||
Таким образом, новые значения величин будут равны: |
= |
− |
||||||||||||||||||||||||
= − |
= |
; |
= |
|
− = |
|
. Сумма затрат составит: |
+ |
+ |
= |
, что со- |
|||||||||||||||
|
|
|
|
|
|
|
∆ |
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||
ответствует искомому значению общих затрат. |
|
|
|
|
||||||||||||||||||||||
······································································· |
||||||||||||||||||||||||||
Модифицированный метод обратных вычислений |
|
|
|
опреде |
||||||||||||||||||||||
Модифицированный метод обратных вычислений заключается |
||||||||||||||||||||||||||
ентов относительной важности. Он предполагает постр ение уравнения связи |
||||||||||||||||||||||||||
лении аргументов функции на основании её указанного значения |
коэффици- |
|||||||||||||||||||||||||
между |
аргументами |
вида |
|
= |
|
± |
|
|
и |
|
подстановку |
полученного уравнения |
||||||||||||||
в исходное соотношение [4]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
||||||
Для построения функции используются следующие формулы ( |
||||||||||||||||||||||||||
функция, |
– начальные значения аргументов): |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
= |
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|

|
В случае обратной |
|
|
|
|
|
|
|
|
между аргументами (один увеличивает- |
||||||||||||
ся – другой уменьшается,зависимости. е. изменение происходит в разных направлениях): |
||||||||||||||||||||||
= + |
|
. В случае прямой зависимости: |
= |
|
− |
. |
|
|
||||||||||||||
|
В итоге получаем уравнение: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
или |
|
|
|
= |
+ |
|
|
|
(в случае прямой зависимости) |
|
|
|||||||||||
В отличие |
= |
− |
|
|
(в случае обратной зависимости). |
|
|
|||||||||||||||
|
т классического метода обратных вычислений он позволяет |
|||||||||||||||||||||
избежать |
|
проверок согласованности дополнительной информации, поступаю- |
||||||||||||||||||||
щей от человека: соответствия поставленной цели коэффициентам важности. |
||||||||||||||||||||||
······················· |
|
|
|
|
|
|
|
|
Пример 2.11 |
······················· |
||||||||||||
|
Рассмотрим пример определения цены и количества проданного товара |
|||||||||||||||||||||
(рис. 1.1) |
|
помощью линейного уравнения (α = |
|
; β = |
). В случае пря- |
|||||||||||||||||
мой зависимости расчет осуществляется следующим образом: |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a = |
|
− |
0,2575 |
|
= − |
|
|
|
|
|
|||
|
Подставляем полученную зависимость в исходную формулу: |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= − |
+ |
|
|
|
|
|
|
|||
|
Решая квадратное уравнение, получим: |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
( |
− |
|
+ |
c)c |
= |
|
|
|
|
|
|
||
2.13,Рассмотрим: = |
также реализацию алгоритма |
|
примере задачи |
рисун- |
||||||||||||||||||
, |
= |
, |
α = |
|
|
, |
|
β = |
. |
Величина, имеющая наименьший |
||||||||||||
коэффициентппропорци нальности – |
|
= |
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
= − |
|
+ |
|
|
= |
|
|
|
|
|
|||
|
Построим линейное уравнение: |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
β |
|
и |
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляем полученное уравнение в исходную формулу зависимости: |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
+ |
|
= |
|
|
|
+ |
= |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
и |
− |
и |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,57 |
= |
|
|
|
|
|
|||||||
|
|
|
|
|
|
= |
|
|
|
− |
|
|
|
|
+ |
|
= |
|
|
|
||

|
|
|
|
|
и = |
|
|
|
|
|
|
Результат совпал с полученным ранее. |
|
|
|
|
|||||||
|
|
|
|
и |
|
|
|
|
|
|
|
Аналогично найдем решение для случая на рисунке 2.13, б: |
|||||||||||
|
= |
− |
|
|
= |
|
|
− |
|
|
= |
Величина |
= |
|
, |
= |
|
, α = |
|
, |
β = |
. |
|
имеетпнаименьший коэффициент пропорциональности. |
|||||||||||
Построим линейное уравнение: |
|
|
|
|
|
|
|
||||
|
|
|
α |
|
|
|
|
|
|
|
|
Подставляем полученное уравнение в формулу: |
|
||||||||||
|
п |
− |
β |
и = |
|
− |
|
|
= |
|
|
|
|
|
|
= |
|
+ |
и |
|
и |
|
|
|
|
|
|
1,43 |
и = |
|
|
|
|||
|
= |
|
+ |
|
|
|
+ |
|
= |
|
|
|
|
|
|
|
|
и = |
|
|
|
|
|
······································································· |
|||||||||||
|
|
п |
|
|
и |
Пример 2.12 ······················· |
|||||
······················· |
+ |
|
|||||||||
|
|
|
= |
|
= |
+ |
|
= |
|
|
|
Также рассмотрим следующий пример завис мости функц |
от трех ар- |
||||||||||
гументов. Прибыль организации ( ) |
равна разности |
выручки ( ) |
иипостоянных |
||||||||
( ) и переменных ( |
) |
затрат: |
|
|
|
|
|
|
. Ставится за |
||
Исходные данные (тыс. руб.): |
|
= |
|
= |
= |
= |
|||||
дача определения уровня выручки, переменных постоянных затрат для увели- |
|||||||||||
чения прибыли на 150 тыс. При этом |
коэффициенты |
относительной значимости |
|||||||||
равны: α = |
|
|
|
|
= |
− |
− |
|
|
|
|
β = |
|
γ = |
(рис. 2.17). |
|
|
|
|
|
|||
Задача может быть решена с помощью процедуры свертк . Нужно опре |
|||||||||||
делить дополнительную переменную |
, характеризующую общие затраты. То |
||||||||||
задача разбивается на две подзадачи (рис. 2.18). Сначала необходимо опре- |
|||||||||||
гдалить прирост выручки |
общих затра , а затем изменение постоянных и |
||||||||||
переменных затрат. |
Значения коэффициентов |
пропорциональности нормируют- |
|||||||||
ся таким образом, чтобы их сумма была равна единице. |
|
|
|||||||||
