
Исследование операций и методы оптимизации
..pdf
|
|
|
|
|
Таблица 3.11 |
|
|
Свободные |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
члены |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
|
… |
|
|
|
… |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
Шаг 1. Среди |
|
столбцов из |
|
коэффициентов |
|
при неизвестных выбирается |
|||||||||||||||
|
|
|
|||||||||||||||||||
столбец, в котором имеется хотя бы один положительный элемент. Если в та- |
|||||||||||||||||||||
м столбце несколько положительных элементов, то из них выбирается тот, |
|||||||||||||||||||||
к торый отвечает наименьшему частному при делении соответствующих сво- |
|||||||||||||||||||||
бодных членов на положительные элементы выбранного столбца. Выделенный |
|||||||||||||||||||||
таким образом элемент называется разрешающим. |
|
|
|||||||||||||||||||
Шаг 2. Элементы разрешающей строки делятся на разрешающий элемент |
|||||||||||||||||||||
и переписываются в новую таблицу. |
|
|
|
|
|
|
|
|
|
|
|
|
следующим обра- |
||||||||
Шаг 3. Каждая новая трока новой таблицы |
|
||||||||||||||||||||
зом: из строки элементов |
исходной таблицы вычитаетс |
разрешающая строка, |
|||||||||||||||||||
полученная на шаге 2, которая предварительно умножаобразуется на соответствую |
|||||||||||||||||||||
щий элемент разрешающего столбца. При этом в клетках выделенного (разре |
|||||||||||||||||||||
шающего) столбца появятся нули. На этом заполнение новой таблицы заканчи- |
|||||||||||||||||||||
вается и происходит переход к шагу 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Процесс продолжается до тех пор, пока не будет получено неотрицатель- |
|||||||||||||||||||||
ное базисное решение. |
|
|
|
|
|
|
Пример 3.9 ······················· |
||||||||||||||
······················· |
|
|
|
|
|
|
|||||||||||||||
Найти неотрицательное базисное решение системы: |
|
|
|||||||||||||||||||
|
|
|
x |
|
|
|
|
− |
x |
|
|
+ |
|
x |
|
= − |
|
|
|||
|
|
|
1 |
x |
|
|
|
|
5 |
|
x |
6 |
|
|
|
|
|
||||
|
|
|
|
x |
|
− |
x |
− x |
= |
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
5 |
|
|
6 |
|
|
|||||||
|
|
|
|
|
x |
− |
|
|
+ x |
|
= − |
|
|
||||||||
|
|
|
|
|
3 |
+ x5 |
− |
x6 |
|
|
= − |
|
|
||||||||
|
|
|
|
|
|
|
|
4 |
|
|
5 |
|
|
|
6 |
|
|
|
|
|
|
Воспользуемся методом симплексного преобразования. Перед состав |
|||||||||||||||||||||
ием начальной |
с целью получения неотрицательных свободных чле |
||||||||||||||||||||
нов первое, третьетаблицычетвертое уравнения умножим на –1. Дальнейшие преобразования по нахождению начального базиса приведены в таблице 3.12.
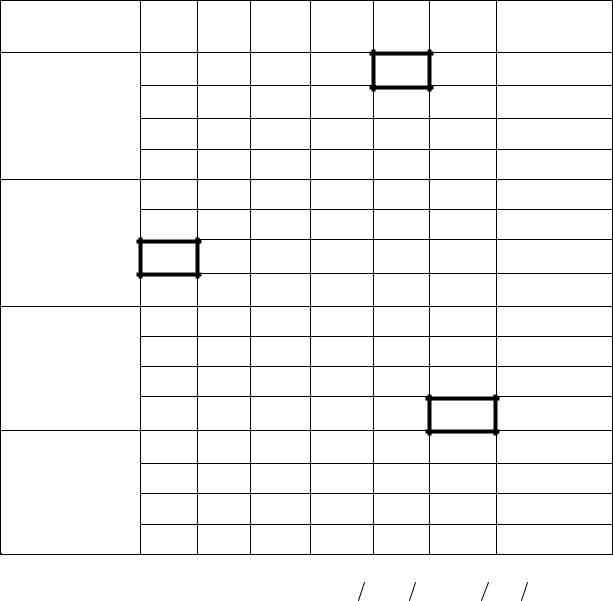
Этап преобра- |
Таблица 3.12 – Этапы решения задачи |
|
Свободные |
||||||
|
зований |
x |
x2 |
x3 |
x4 |
x5 |
x6 |
члены |
|
Этап 1 |
–1 |
0 |
0 |
|
5 |
|
2 |
3 |
|
|
|
|
1 |
0 |
–2 |
–1 |
5 |
||
|
|
0 |
|
–1 |
3 |
7 |
|||
Этап 2 |
0 |
|
–1 |
–1 |
3 |
4 |
|||
1 |
0 |
|
1 |
2 |
3/5 |
||||
|
|
–2/5 |
1 |
0 |
|
–9/5 |
31 |
||
|
|
3/5 |
|
–1 |
0 |
1/5 |
6 |
||
Этап 3 |
–1/5 |
0 |
0 |
–1 |
13 |
23/5 |
|||
|
|
0 |
1 |
2 |
0 |
|
–5/3 |
26 |
|
|
|
1 |
|
5 |
0 |
1 |
|
||
Этап 4 |
|
0 |
1 3 |
–1 |
8/3 |
19 3 |
|||
0 |
3 |
1 |
1 |
|
|
25/8 |
|||
|
|
1 |
–7/8 |
–5/8 |
|
0 |
109/8 |
||
|
|
1 |
0 |
–13/8 |
1/8 |
0 |
63 |
||
|
|
0 |
–1/8 |
–3/8 |
1 |
19/8 |
|||
|
Итак, получили базисное решение |
( |
|
|
|
), что при |
|||
необходимости позволяет составить первую симплекс-таблицу с начальным ба- |
|||||||||
зисом |
|
|
|
= ( |
|
) |
|
|
|
|
В канонической системе каждому уравнению соответствует ровно одна |
||||||||
базисная переменная. |
|
|
|
|
|
|
|
||
······································································· |
|||||||||
Метод искусственного базиса |
|
|
|
|
|
|
|||
|
Другим методом поиска начального базиса является метод искусственно- |
||||||||
го базиса [1]. |
|
|
|
|
|
|
|
|
|

|
В систему ограничений |
|
|
вводятся |
|
|
|
искусственные |
переменные |
xn+i ≥ |
||||||||||||||||||||
( = |
) и вводится искусственная целевая функция |
( ) = |
m |
. Таким |
||||||||||||||||||||||||||
образом, приходим к следующей задаче линейного программирования |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z(x) → min, |
|
|
|
|
|
|
|
i=1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ + |
(3.20) |
||||||||||||||
|
|
|
∑ ij |
j + |
|
n+i |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
= |
|
|
|
|
|
|
= |
|
|
|
|
|
||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее ищется решение задачи (3.20) симплекс-методом. В качестве бази а |
|||||||||||||||||||||||||||||
спользуются переменные |
+ |
. В процессе решения переменные |
+ выводятся |
|||||||||||||||||||||||||||
из базиса, а переменные |
|
k |
≥ |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
||||
|
вводятся |
|
|
|
базис. Процесс поиска заканчивается, |
|||||||||||||||||||||||||
когда все переменные |
+ |
будут выведены |
из базиса, при этом значение искус- |
|||||||||||||||||||||||||||
ственной целевой функции |
|
|
|
|
|
обращается в ноль. |
······················ |
|||||||||||||||||||||||
······················· |
|
|
|
|
|
|
|
|
|
|
Пример 3.10 |
|||||||||||||||||||
|
Найти неотрицательное базисное решение системы: |
|
|
|
||||||||||||||||||||||||||
|
|
|
−x |
|
|
|
|
|
|
+ |
|
x |
|
|
|
− |
x |
|
= |
|
|
|
|
|
|
|||||
|
|
|
|
1x |
|
− x |
|
|
− |
5x |
|
− x6 |
= |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
+ |
|
x5 |
− x6 |
= |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
− x |
|
− x |
5 |
+ |
|
|
|
x |
= |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
ные |
|
|
|
Введем в систему ограничений4 дополнительные5 6 |
|
|
|||||||||||||||||||||||||||
|
которые будем называть искусственными. В результатпеременполучим систему: |
|||||||||||||||||||||||||||||
|
|
|
−x |
|
+ |
x |
|
− |
|
x |
|
+ x |
|
= |
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
1 |
− |
x |
|
− x |
|
|
|
+ x |
|
|
|
= |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
5 |
|
− x6 |
6 |
|
|
|
7 |
|
|
|
|
|
|
|
||||||||
|
|
|
−x2 |
+ |
|
x5 |
|
|
+ x8 |
|
= |
|
|
|
|
|
|
|||||||||||||
|
|
|
−x |
3 |
− x |
|
+ |
|
x |
6 |
+ x |
9 |
|
= |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Запишем искусственную целевую функцию: |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
5 |
|
|
|
|
6 |
|
|
|
10 |
|
|
|
|
|
|
|
|||||
|
Из системы ограничений выразим дополнительные переменные |
|
||||||||||||||||||||||||||||
|
через исходные, получим: |
= |
|
|
+ |
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= + − + = − + +

|
|
|
|
= |
+ |
− |
+ |
|
|
|
|
|
|
|
|
|
= |
+ |
+ |
− |
|
|
|
|
|
Подставим в целевую функцию, получим: |
|
|
|
|
|
|||||||
Дальше реша |
|
= |
+ |
− |
+ |
+ |
− |
+ |
|
|
ис |
|
задачу симплекс-методом. В результате реш ния |
||||||||||||
кусственные переменные должны выйти из базиса. Решение приведеновсетаб- |
||||||||||||
лице 3.13. |
Таблица 3.13а – Решение задачи (первая итерация) |
|
|
|||||||||
|
|
|
Небазисные переменные |
|
Свободные |
|
||||||
|
|
|
|
|
|
|
|
|
|
члены |
|
|
|
|
–1 |
↓ |
|
0 |
0 |
|
5 |
–2 |
|
3 |
|
|
|
0 |
|
|
|
|
||||||
|
→ |
0 |
1 |
|
0 |
0 |
|
–2 |
–1 |
|
5 |
|
переменныеБазис |
|
0 |
0 |
|
–1 |
0 |
|
3 |
–1 |
|
7 |
|
|
0 |
0 |
|
0 |
–1 |
|
–1 |
3 |
|
4 |
|
|
Целевая |
|
|
|
|
||||||||
1 |
–1 |
|
1 |
1 |
|
–5 |
1 |
|
–19 |
|
||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.13 – Решение задачи (вторая итерация) |
|
|
|||||||||
|
|
|
Небазисные переменные |
|
Свободные |
|
||||||
|
|
|
|
|
|
|
|
|
|
члены |
|
|
|
|
–1 |
0 |
|
0 |
0 |
|
↓ |
–2 |
|
3 |
|
|
→ |
|
|
5 |
|
|
||||||
|
|
|
1 |
|
0 |
0 |
|
–2 |
–1 |
|
5 |
|
переменныеБазис |
|
0 |
0 |
|
–1 |
|
3 |
|
7 |
|
||
|
|
0 |
–1 |
|
1 |
3 |
|
4 |
|
|||
Целевая |
|
|
|
|
||||||||
1 |
1 |
|
1 |
1 |
|
–7 |
0 |
|
–14 |
|
||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.13в – Решение задачи (третья итерация) |
|
|||||||||||
|
|
|
Небазисные переменные |
|
|
Свободные |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
члены |
|
|
|
1 |
0 |
|
|
|
1 |
|
|
↓ |
|
3/5 |
|
|
|
0 |
|
|
|
|
2 |
|
|||||
|
|
–2/5 |
1 |
|
0 |
2/5 |
|
–9/5 |
|
31 |
|||
переменныеБазис |
|
3/5 |
0 |
–1 |
|
–3/5 |
|
|
1/5 |
|
26/5 |
||
→ |
–1/5 |
0 |
0 |
|
–1 |
1/5 |
|
13/5 |
|
23/5 |
|||
|
|
|
|
||||||||||
Целевая |
–2/5 |
1 |
1 |
|
1 |
7/5 |
–14/5 |
|
–49/5 |
||||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.13г – Решение задачи (четвертая итерация) |
|
|||||||||||
|
|
|
Небазисные переменные |
|
|
Свобод- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
ные чле- |
|
|
|
|
0 |
|
|
2 |
|
|
|
2 |
|
|
ны |
|
|
↓ |
0 |
|
7/13 |
|
|
17/13 |
|||||
|
|
–7/13 |
1 |
–9/13 |
|
9/13 |
|
122/13 |
|||||
переменныеБазис |
→ |
8/13 |
0 |
–1 |
|
1/13 |
–8/13 |
|
–1/13 |
63/13 |
|||
|
–8/13 |
0 |
0 |
|
5 |
21/13 |
|
5/13 |
|
23/13 |
|||
Целевая |
|
|
|
||||||||||
1 |
1 |
–1/13 |
|
14/13 |
–63/13 |
||||||||
функция |
Таблица 3.13д – Решение задачи (результат) |
Свобод- |
|||||||||||
|
|
|
Небазисные переменные |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ные чле- |
|
|
|
3 |
0 |
3 |
|
1 |
|
|
|
1 |
|
|
ны |
|
|
|
|
0 |
|
|
25/8 |
||||||
|
|
7/8 |
1 |
–7/8 |
|
–5/8 |
|
5/8 |
|
109/8 |
|||
переменныеБазис |
|
13/8 |
0 |
–13/8 |
1/8 |
–1 |
|
–1/8 |
|
63 |
|||
|
1/8 |
|
–1/8 |
|
–3/8 |
0 |
|
3/8 |
|
19/8 |
|||
Целевая |
1 |
|
|
|
|||||||||
0 |
|
0 |
|
1 |
|
1 |
|
|
0 |
||||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|

|
Итак, получили базисное решение |
( |
|
|
|
|
|
|
|
|
). Это базис- |
|||||||||||||||||||||||||||||||
ное решение совпало с решением, полученным симплексным преобразованием |
||||||||||||||||||||||||||||||||||||||||||
таблицы ограничений. Значение искусственной целевой функции рано нулю. |
|
|||||||||||||||||||||||||||||||||||||||||
|
В результате получим следующую систему уравнений-ограничений: |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
− |
|
|
|
|
|
|
x |
|
+ |
|
|
|
|
|
x |
|
= |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
x |
|
4 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
x2 |
|
|
− |
|
|
|
|
x3 |
|
|
− |
|
|
|
|
x4 |
|
|
= |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
x5 |
|
− |
|
|
|
|
x3 |
|
− |
|
|
|
x4 |
|
= |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||
·········································· · ···························· |
||||||||||||||||||||||||||||||||||||||||||
|
Рассмотрим случай, когда часть ограничений задана в виде неравенств, |
|||||||||||||||||||||||||||||||||||||||||
а часть ограничений – в виде равенств: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
n |
∑ ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
∑ ij |
|
|
|
j |
|
|
|
|
|
i |
|
j =1,...,n. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
j=1 |
|
|
|
x |
|
|
|
≥ |
0, |
|
|
n+i |
|
|
, |
||||||||||||||||||||||||
|
Дополним неравенства |
|
дополнительными |
= |
x + |
|||||||||||||||||||||||||||||||||||||
а ограничения равенства дополним |
|
|
искусственнымипеременнымиеменными |
|
+ |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j |
= |
|
|
|
|
|
|
|
|
= |
|
|
|
+ |
|
|
|
|
|
|
|
|
||||||||
= |
|
− . В результате мы получим систему ограничений в стандартной |
||||||||||||||||||||||||||||||||||||||||
форме: |
|
n |
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
n+i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
∑ ij |
|
|
|
|
+ |
|
|
= |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||||||||||||||
|
|
n j=1 |
|
|
j + |
|
|
|
|
n+i |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
∑ ij |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= + |
|
|
|
|
|
|
||||||||||||||||||
|
|
j=1 |
|
|
|
x |
|
|
|
≥ |
0, |
|
j |
=1,...,n + m. |
|
|
|
|
||||||||||||||||||||||||
|
Затем рассматривается вспомогательная задача: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
z x |
|
= |
|
|
m |
|
|
|
|
|
|
→ |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
∑ |
|
|
|
n+i |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=k |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
n+i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
∑ ij |
|
|
|
|
+ |
|
|
= |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||||||||||||||
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
n |
|
|
j + |
n+i = |
i = + |
|
|
|
|
|||
|
|
|
|
∑ ij |
|
|
|
|
||||||||
|
|
|
|
j=1 |
|
j |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
≥ |
= |
|
+ |
|
|
|
|
||
|
В качестве начального базиса используются переменные |
= |
||||||||||||||
В процессе решения искусственные переменные выводят |
из базисаn+i. При этом |
|||||||||||||||
дополнительные переменные |
|
n+i |
= |
|
должны |
остаться |
базисе. На по- |
|||||||||
следнем шаге симплекс-метода значение искусственной целевой |
функции будет |
|||||||||||||||
равно нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.4 Задачи многокритериальной оптимизации |
|
|
|
|||||||||||||
в |
В практической деятельности часто встречаются задачи, заключающиеся |
|||||||||||||||
|
лучшего (оптимального) решения |
|
наличии различных |
|
||||||||||||
другпоискедругу |
|
оптимальности. |
Например, принятие решениянесводимыхстрои |
|||||||||||||
тельстве дорогикритериев |
|
города должно учитывать такие факторы, как выиг |
|
|||||||||||||
рыш города в целомобъездсоображениям экологии, проигрыш отдельных пред- |
||||||||||||||||
|
риятий |
фирм, |
например, |
из-за уменьш ния проезжающих через город |
||||||||||||
потенциальных покупател й, |
|
многие |
другие. Если такого рода задачи реша |
|
||||||||||||
ются методами математического программирования, то говорят о задачах мно- |
||||||||||||||||
гокритериальной оптимизации. Эти задачи могут носить как линейный, так и |
||||||||||||||||
нелинейный характер. Далее будем рассматривать только линейные задачи [1]. |
|
|||||||||||||||
|
Задачи многокритериальной оптимизации возникают в тех случаях, когда |
|||||||||||||||
имеется несколько целей, которые не могут быть отражены одним критерием |
||||||||||||||||
(например, стоимость |
надежность). Требуется найти допустимое решение, |
|||||||||||||||
которое минимизирует или |
максимизирует все такие критерии. Если в подобно- |
|||||||||||||||
го рода задачах речь идет не о разнородных критериях некоторой системы, |
|
|||||||||||||||
сопоставлении однородных критериев разных ее подсистем (например, отрасли, |
||||||||||||||||
группы населения и т. п.), то эти |
задачи называются задачами векторной оп- |
|||||||||||||||
тимизации. |
-й частный критерий через |
|
), где |
– допустимое ре- |
||||||||||||
шение,Обозначимобласть д |
( |
|||||||||||||||
пустимых |
|
ешений – через |
i . Задачу многокритериальной |
|||||||||||||
оптимизации можно сформулировать следующим образом: |
|
(3.21) |
||||||||||||||
|
|
( |
) = { |
1 |
( |
) |
|
2 |
( ) |
m |
( |
)} → |
|
|
||
Некоторые частные критерии могут противоречить друг другу, другие действуют в одном направлении, третьи – индифферентны, безразличны к
другу. Поэтому процесс решения |
|
|
|
|
|
|
адач неизбежно связан |
|||||||||
с экспертными оценками как самих критериев, так |
взаимоотношений между |
|||||||||||||||
ними. Известен ряд методов решениямногокритериальныхзадач риальной оптимизации: |
||||||||||||||||
• |
оптимизация одного пр зн нного |
наиболее важным критерия, осталь- |
||||||||||||||
|
ные критерии при этом играют роль |
|
|
|
|
ограничений; |
оп |
|||||||||
• |
упорядочениетимизация |
заданного множества критериевдополнительныхпослед |
|
|||||||||||||
|
каждому из них (этот подход рассмотреновательнаяниже при- |
|||||||||||||||
|
мере |
последовательных уступок); |
|
|
|
|
|
|||||||||
• |
сведениеметодаогих критериев к одному введением экспертных весовых |
|||||||||||||||
|
коэффициентов для каждого из критер |
ев таким образом, что более |
||||||||||||||
|
важный критерий получает б лее |
высокий |
вес; |
|
|
|
|
|||||||||
• |
метод справедливого |
компромисса, |
который допускает |
|
|
|||||||||||
|
важность всех частных |
|
|
|
не требует их нормализацииодинаковую |
|||||||||||
|
упорядоченности по степеникритериевжности. |
|
|
|
|
|
|
|||||||||
Для решения задач многокритериальной оптимизации используют крите |
||||||||||||||||
рий оптимальности Парето, суть которого состоит в улучшении одних показа- |
||||||||||||||||
телей при условии, чтобы другие не ухудшались. |
|
|
|
|
|
|
||||||||||
Вектор |
* |
называется эффективным (оптималь ым по Парето) реше- |
||||||||||||||
нием задачи (3.21), если для любого вектора |
|
выполняется соотношение |
||||||||||||||
|
|
|
|
|
i ( |
) ≤ |
i ( |
* ) |
= |
|
|
|
|
. |
|
|
причем хотя бы для одного значения |
|
имеет место строгое |
|
|
||||||||||||
Множество допустимых решений, для которых |
|
неравенствоодновремен- |
||||||||||||||
но улучшить все частные показатели эффективностиневозможн(т. . улучшить хотя бы |
||||||||||||||||
дин из них, не ухудшая |
|
|
принято называть |
областью Парето, |
или |
|||||||||||
бластью компромиссов,остальных),принадлежащие ей решения – эффективными, |
||||||||||||||||
оптимальными по Парето. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Метод уступок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим один из методов решения многокритериальных задач – метод |
||||||||||||||||
последовательных уступок [1]. |
уступок решения |
задач многокритериальной |
||||||||||||||
Метод |
оследовательных |
|||||||||||||||
оптимизации |
применяется |
случае, когда частные критерии могут быть упоря |
||||||||||||||
дочены в порядке |
|
|
их важности. Предположим, что все частные кри- |
|||||||||||||
терии максимизируютсяубыванияпронумерованы в порядке убывания их важности.
Находим максимальное значение |
|
|
|
|
|
первого по важ сти критерия в области |
|||||||||||||||
допустимых решений путем решения однокритериальной задачи: |
|
||||||||||||||||||||
|
|
|
Z |
|
X |
|
|
|
→ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
( |
|
|
X) |
S. |
|
|
|
принятой точности, назна- |
||||||||
|
Затем, исходя из практических соображений |
||||||||||||||||||||
чается величина |
отклонения |
∆1 |
> |
(экономически |
оправданной |
||||||||||||||||
уступки) критериядопустимого, далее находится максимальное значение второго кри- |
|||||||||||||||||||||
терия |
при условии, что значение первого критерия не должно отклоняться от |
||||||||||||||||||||
|
максимального значения более, чем на величину допустимой уступки, |
||||||||||||||||||||
своегот. . решается задача: |
|
Z |
2 |
|
|
X ) → |
|
|
|
|
|
|
|
||||||||
|
|
|
( |
|
|
|
|
|
|
|
|||||||||||
|
|
Z |
(X ) |
≥ Z |
* |
|
− ∆ |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
X |
S. |
|
|
|
по второму критерию, кото |
||||||||
|
Снова назначается величина уступки |
∆ |
|
> |
|||||||||||||||||
рая вместе с первой уступкой используется для нахождения условного макси- |
|||||||||||||||||||||
мума третьего частного критерия: |
|
|
|
X ) → |
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
Z3 |
( |
* |
|
− ∆ |
|
|
|
|
||||||||||
|
|
Z |
( |
X ) |
≥ Z |
|
|
|
|
|
|||||||||||
|
|
Z |
( |
|
|
|
) |
≥ |
|
* |
|
− ∆ |
|
|
|
|
|||||
|
Аналогичные процедуры |
|
|
|
|
|
|
X |
S. |
|
до тех пор, пока не будет выявлено |
||||||||||
максимальное значение последнегоповторяютсяважности |
ия |
при условии, что |
|||||||||||||||||||
значение каждого из первых |
|
− |
|
|
частных критериев отличается от соответ |
||||||||||||||||
ствующего условного максимума не более чем на величину допустимой уступ- |
|||||||||||||||||||||
ки по данному критерию. Полученное на последнем этапе решение считается |
|||||||||||||||||||||
оптимальным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим пример решения задачи многокритериальной оптимизации |
||||||||||||||||||||
методом последовательных уступок. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пусть задача трехкритериальной оптимизации имеет вид: |
2) |
|||||||||||||||||||
|
Z |
= −x |
|
+ |
|
x |
|
|
→ |
|
|
|
|
||||||||
|
Z |
|
= |
|
|
x |
|
+ |
x |
|
→ |
|
|
|
|
3) |
|||||
|
Z |
|
= x |
1 |
− |
|
|
|
→ |
|
|
|
|
(3.24) |
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
3 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
x |
120 |
|
|
|
|
|
+ x |
≤ 6; |
(3.25) |
|
|
|
|
1 |
≤ x2 |
≤ 3; |
|
|
|
|
1 |
≤ x1 |
≤ 4. |
|
Заметим, что . . коэффицие ты2при одних и тех же переменных в дан |
||||||
ных частных критериях имеют |
разные знаки, то в заданной области |
- |
||||
мых решений невозможно |
дновременно улучшить все частные критерии,допусти. е. |
|||||
в рассматриваемом случае |
область компромиссов (область Парето) совпадает с |
|||||
областью допустимых решений. |
|
|
|
|
|
|
Для определен ости будем считать, что допустимые уступки по первым |
||||||
двум критериям заданы: ∆1 |
= 3; |
∆2 |
= |
5 3. |
|
. . реша |
Максимизируем функцию |
Z |
в области допустимых решений, |
||||
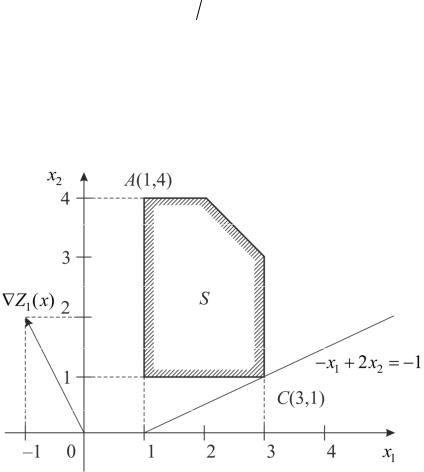
ем однокритериальную задачу (3.22),1 (3.25). Это несложно сделать рассмотренным ранее графическим методом решения задач линейного программирования (см. рис. 3.13).
функции |
Z |
|
при |
|
(3.25) достигается в точке A обла- |
||||
сти S Максимумкоординатами (1;4), так чтоусловияхданном случае |
|
||||||||
|
1 |
|
|
|
|
(A) = 7. |
|
||
|
x* |
=1; x* = 4; Z* = Z |
|
|
|||||
Переходим к максимизации функции |
Z |
|
|
при условиях (3.25) и дополни- |
|||||
|
1 |
|
2 |
1 |
1 |
|
|
Z нельзя усту- |
|
тельном ограничении, позволяющем учесть, что по критерию |
|||||||||
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
