Исследование операций и методы оптимизации

УДК

[519.

+ 519.85](075.8)

ББК

22.183.41я73

Рецензенты:

Г 820

А. А. Шелестов, канд. техн. наук, доцент кафедры автоматизированных систем

управления Томского государственного у

верситета систем

О. Л.

управления и радиоэлектроники;

, канд. физ.-мат. наук, доцент кафедры высшей математики

Крицкийматематической физики Национального исследовательского

Томского политехнического университета

Г 820

Грибанова Е. Б., Мицель А. А.

Исследование операций и методы оптимизации / Е. Б. Грибано-

ва, А. А. Мицель. – Томск : ФДО, ТУСУР, 2017. – 185 с.

В пособии рассматриваются основные понятия исследования операций,

методы нахождения минимума одн мерной

многомерной

функций, также способы решения задачи линейного

нелинейного

програм

представленымирования,

нсп ртной задачи, братной задачи. Пр

ведены при

еры ис-

пользования

рассмотренных методов для решения

различных

экономических

задач.

Оглавление

5

Введение ..................................................................

функций

1 Методы одномерной

7

1

Основные

оптимизацииопределения................

.......................................

2

Необходимыепонятиядостаточные условия существования экстремума

2

3

Характеристики алгоритмов оптимизации

3

1.4

Прямые методы поиска минимума

5

1

равномерного поиска

2

дихотомии...........

17

3

Метод

золотого сечения

0

1.4.4

Пауэлла ...........................................................

2

1.5

Методы, основан ые на использовании производных

6

1

Метод

Ньютона.........

1.5.2

средней точки................................

7

6

Решение задачи опре еления цены на товар....

29

1.7

Сравне ие метод в

одномерной оптимизации

1

2 Методы многомерной оптимизации функций

3

2.1

Методы прямого поиска

1

Метод Гаусса............

4

2

Симплексный метод ..

36

2.

.1.3

Метод Хука – Дживса

2

методы ...

6

Градиентные1 тный спуск..........................................

49

2

Метод

наискорейшего спуска (метод Коши)

0

3

Ньютона...............................

..............

4

2.2.4

З дача определения параметров регрессии....................

5

3

Глобальная оптими

ция с

помощью

случайных величин ....

6

2.4

Решение обратных задач с

обратных вычислений

59

3 Линейное программирование.....................................

3

1

остановка

дачи

ейного программирования

3.2

Примеры задач линейного

программирования...................................

78

3.2.1 Задача об использовании ресурсов (задача планирования

78

2

производ

ва).................................................................................

Задача

составления рациона (задача о диете, задача о смесях)..

83

3.2.3

использовании мощностей

87

(задачаобзагрузке оборудования)

..................................................

4

раскрое материалов...

88

5

технического контроля ............

0

3.

.2.6

Задача об оптимальн м ассортименте.......

1

Решение задач лин йного программирования....................................

92

3.3.1 Графический метод решения задач линейного

2

2

программирования...........

Основы симплекс-метода....

6

3

Алгоритм симплекс-метода

..99

3.3.4

Поиск начального базиса .......................

0

3.4

Задачи многокритериальной оптимизации

17

4 Транспортная задача

..................................................................

25

1

Экономико-математическая модель транспортной задачи

2

Решение транспортной задачи симплексным методом ............

36

3

Первоначальное закрепление потребителей за поставщиками

4

Метод потенциалов............................. ....

4.5

Открытая модель транспортной задачи

146

5 Целочисленное программирование......................................................

5.1

Графический метод решения задач целочисленного

6

5.2

программирования

Метод Гомори............................................

использованием СМ

48

3

1

Алгоритм МГ

.....................................

Метод ветвейчастичнограниц

54

5.2.2

Решение

целочисленных задач методом Гомори

2

4

назначениях....

3

5

Задача о коммивояжере

66

5.6

Метод Монте-К рло ................................................

170

6 Нелинейное программирование.............................Задачи с ограничениями

в виде равенств........................

4

1

замены переменных....

2

Метод множи елей .............................................................Лагранжа

175

6.3

Решение обратной

задачи с помощью метода множителей

78

Лагранжа

Заключение

1

Литература................

2

Список сокращений

3

Глоссарий......................................................................................................

184

Введение

Исследование операций изучает применения количественных методов

для управления сложными системами людей, машин, материалов, денег и ин-

формации. Методология исследования операций позволяет понять сущность

управленческих проблем и разработать модели для оценки последствий прини-

маемых решений.

операций» как самостоятельная

дисциплина воз

никло годы Второй мировой войны, когда для решенинаучнаясложных проблем ло-

гистики«Исследованиепроектирования систем вооружений создавались команды практиков,

в которые вх дили специалисты из самых различных областей: математики,

инженеры, экономисты,

психологи т. д. Эти команды анализировали

фор

мулировали проблему в

количественных терминах, чтобы найти ее оптималь-

ное решение. Сегодня методы исследование операций широко используются

в операционном менеджменте и других бизнес-ориентированных дисциплинах.

Соглашения, принятые в учебном пособии

Для улучшения восприятия материала данном учебном пособии исполь-

зуются пиктограммы и специальное выделение важной информации.

·····························································

Эта пиктограмма означает определение или новое понятие.

·····························································

Эта пиктограмма означает «Внимание!». Здесь выдел на важ

ная информация, требующая акцента на ней. Автор может

поде-

·····························································

Эта пиктограмма означает совет. В данном блоке можно ука-

ть более простые или иные способы выполнения определенной

задачи. Совет

может касаться практического

ия только

что изученного или содержать указания на то,примененкак много повы

сить эффективность и значительно упростить выполнение некото-

рых задач.

·····························································

Эта пиктограмма означает теорему.

·····························································

························

Пример ··························

Эта пиктограмма означает пр мер. В данном блоке автор может привести

практический пример для

пояснения и разбора основных моментов, отражен-

ных в теоретическом материале.

1 Методы одномерной7оптимизации функций

1.1 Основные понятия и определения

простейшие

минимизации, в которых целевая функ-

ция зависитРассмотримодной переменной,задачидопустимым множеством является отрезок

вещественной оси [1, 2]:

f (x) → min;

x [a;b].

·······················································································

Число x* [a;b]

называется точкой глобального

-

ного) минимума, или просто точкой минимума, функции(абсолютf x) на

отрезке [a;b], если

f

x*

≤ f (x) для всех x [a;b].

·······················································································

На рисунке 1.1 точка M

– глобальный минимум, точка N – глобальный

максимум.

(

)

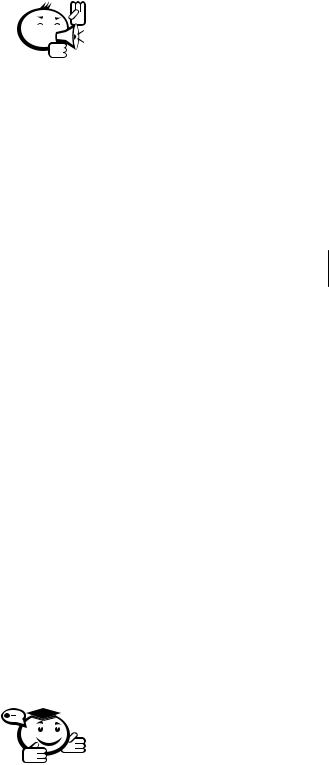
На рисунке 1.1 точки

и

– локальные минимумы.

·······················································································

Любая точка глобального минимума целевой функции (ЦФ)

является одновременно

точкой локального ми имума этой

функции. Обратное

утверждение, вообще говоря, неверно.

·······················································································

Точность. Характеристикой точности полученного решения может слу-

жить величина абсолютного

значения минимизируемой функции,

достигнутого в точке

n

отклонения, точного значения ее минимума на отрезке

:

n

*

n *

δ =

−

Ясно, что чем меньше

неотрицательная величина , тем точнее получен-

δ

ное решение. Недостатком использования абсолютной погрешности является то

(

)

(

)

обстоятельство, что она меняется при умножении ЦФ на положительную кон-

станту

α :

Целесообразнее использовать следующую оценку точности:

f

(xn )− f (x* )

→ α

где

f (x* )

= δ

(

) – либо точное значение минимума ЦФ, либо полученное «точным»

алгоритмом.

и. Многие методы оптимизации

только

Унимодальные

тогда, когда целевая функция

является унимодальной, тприменимы. . любой локаль-

ный минимум ЦФ одновременно является и глобальным.

·······················································································

Функция

является

унимодальной, если слева от

она

монотонно убывает, справа – монотонно возрастает.

·······················································································

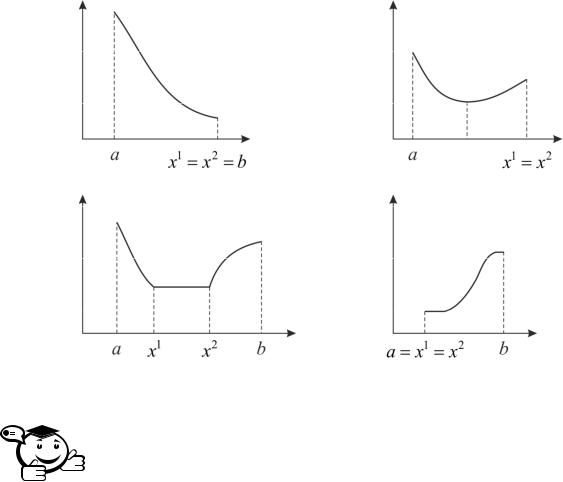
На рисунке 1.2 изображены графики унимодальных функций. Пример

функции, не являющейся унимодальной, приведен на рисунке 1.1.

·······················································································

Функция f (x)

называется унимодальной

на отрезке [a,b],

1

x

2

, удовле-

если она непрерывна на [a,b] и существуют числа x и

творяющие условию a ≤ x1

≤ x2 ≤ b , такие, что:

1)

на отрезке

1

f (x) монотонно убывает;

a, x

функция

2)

отрезке

2

функция f (x) монотонно возрастает;

x

, b

3)

1

2

имеем

f (x

*

)= f

*

= min f (x) .

при x x , x

[a,b]

·······················································································

1

1 2

что возможно вырождение

точку одного или двух из отрезков

и

x

2

, b

. Некоторые варианты расположения и вырождения

a, x

Отметим,x x

точку отрезков монотонности и постоянства унимодальных функций пред-

ставлены

на рисунке 1.2.

f (x) не является

Очевидно, что в некоторых вырожденных случаях ЦФ

дифференцируемой на отрезке [a,b].

f (x)

на практике обычно ис-

Для проверки унимодальности функции

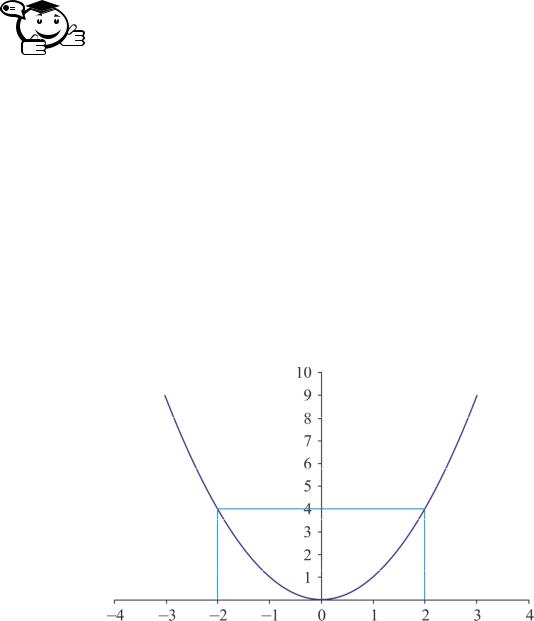
если функция

10

и производная

•

f (x) дифференцируема на отрезке [a,b]

f ′(x) не убывает на этом отрезке;

•

если функция

f (x) дважды дифференцируема на отрезке [a,b] и вто-

рая производная f ′′(x)

≥ 0

при

x [a,b].

f (x) является мульти-

Если эти критерии не выполняются, то функция

модальной

или многоэкстремальной.

Выпуклые функции.

·······················································································

Функция f (x)

выпукла

(«вниз») на

[a,b], если справедливо

неравенство Иенссена:

− µ)x

≤ µ f (x )+ (1− µ) f (x

),

f µ x + (1

2

2

1

и µ [0,1].

для произвольных

x1,x2

[a,b]

·······················································································

Геометрически это означает,

что

все

точки функции

f (x)

для всех

x [a,b] лежат ниже прямой

µ f

(x1 )

+ (1

− µ) f

(x2 ).

то на

любом

отрезке

[x ;x

Если

функция

f (x)

–

выпуклая

на

[a;b],

] [a;b] ее график расположен не выше хорды, проведенной через точки

графика с абсциссами x′ и x′′ (рис. 1.3).

′ ′′

Величина µ x1 + (1− µ)x2

определяет множество=точек x на интервале

[a;b]. При µ, равном единице, мы получим точку

x

, в случае если µ равно ну-

1