
Исследование операций и методы оптимизации
..pdf
CT-1 |
5 |
2 |
20 |
CT-3 |
1 |
–1/2 |
1 |
→ |
|
||||||
|
8 |
4 |
38 |
|
–2 |
5 |
15 |
|
–7 |
–3 |
0 |
|
1 |
1/4 |
59/2 |
|
↓ |
|
|
|
|
|
|
CT-2 |
1/5 |
2/5 |
4 |
|
|
|
|
→ |
|
|
|
|
|||
–8/5 |
4/5 |
6 |
|
|
|
|
|
|
7/5 |
↓ |
|
|
|
|
|
|
–1/5 |
28 |
|
|
|
|
|
|
|
Рис. 5.2 – Симплекс-таблицы |
|
|
|||
|
|
СТ-4 |
1 |
–1/2 |
15/2 |
|
|
|
|
|
|
|
|||
|
|
|
–2 |
5/4 |
|
|
|
|
|
|
↓ |
|
|
|
|
|
|
→ |
0 |
–1/4 |
–1/2 |
|
|
|
|
CT-5 |
1 |
1/4 |
59/2 |
|
|
|
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
–2 |
5 |
5 |
|
|
|
|
|
0 |
4 |
29 |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
Рис. 5.3 – Симплекс-таблицы |
|
|
|||

|
Повторив процесс решения симплексным |
|
етодом для данной расширен |
||||||||||||||||||||||||||||||||
ной системы ограничений, получим новый оптимальный план, в котором пере |
|||||||||||||||||||||||||||||||||||
|
|
входящие в базис, принимают целые |
|
|
|
|
|
|
x |
= |
|
x = |
x = |
. Та |
|||||||||||||||||||||
менные,к образом, приобретение двух машин типазначения:А пяти машин типа Б обеспе |
|||||||||||||||||||||||||||||||||||
ч |
максимум |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
4 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
участка, равный 29 тыс. единиц продук |
||||||||||||||||||||||
цииваетсмену. Заметим,производительностичто если бы качестве плана был выбран вариант, полу |
|||||||||||||||||||||||||||||||||||
чаемый в результате округления первоначального решения задачи симплекс- |
|||||||||||||||||||||||||||||||||||
ным методом |
|
x = |
|
x |
= |
|
, то суммарная производительность была бы равна |
||||||||||||||||||||||||||||
лишь 28 тыс. единиц продукции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
( |
1 |
|
2 |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
······································································· |
|||||||||||||||||||||||||||||||||||
5.2.2 Решение частично целочисленных задач методом Гомори |
|
||||||||||||||||||||||||||||||||||
|
Если |
|
|
|
|
|
|
целочисленности подчинены не все переменные ЗЛП, |
|||||||||||||||||||||||||||
то такая задачатребованиюназыв |
|
ся частично целочисленной [1]. |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Для р шения |
частично |
|
целочисленных задач также используется метод |
|||||||||||||||||||||||||||||||
Гомори, |
|
его |
алгоритм в этом случае отличается видом коэффициентов α + |
||||||||||||||||||||||||||||||||
в |
дополнительной строке: |
|
x |
|
|
|
α |
|
|
|
… α |
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Если переменная |
|
|
подчинена требованию |
|
целочисленности, то имеем |
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n+ |
|
|
n+ |
m+ |
|
|
n+ n |
|
n+ |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
a) |
|
|
|
|
|
|
|
−a , |
|
|
|
|
|
|
a |
rj |
≥ |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
brj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Если же переменная |
n+1, j |
|
|
|
1 |
brj} |
arj , |
|
|
|
a |
rj < |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
−{ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
не подчинена требованию целочисленности, тогда |
||||||||||||||||||||||||||||||||
|
|
|
|
|
б) α |
|
|
α |
|
|
|
= |
|
{ rj} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
= |
|
|
b |
}, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
n+1, j |
|
|
{ |
|
rj |
|
|
|
|
|
|
|
|
|
{ |
|
rj}≤ { |
|
r} |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
{ |
r} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Вычисления заканчиваются, когда целыми являются необязательно все |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
({ }−1), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
коэффициенты |
|
|
|
|
|
1 |
− |
|
|
|
|
{ }> { } |
|
, подчи- |
|||||||||||||||||||||
, а только те, которым соответствуют переменные |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ r} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ненные требованию целочисленности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
······················· |
|
|
|
|
|
|
|
|
|
|
|
Пример 5.3 |
······················· |
|||||||||||
Решить частично целочисленную задачу линейного программирования. |
||||||||||||||||||||||||
|
|
|
|
f (x) = x |
|
− |
|
|
x |
2 |
→ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
+ x |
2x |
≤ |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
− x1 |
|
+ |
|
|
2 |
≤ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
j |
≥ |
|
|
|
|
|
x |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
Запишем задачу в каноническом виде: |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
f (x) = x |
|
− |
|
|
x |
2 |
→ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
+ x |
|
|
|
|
|
||||||
|
|
|
|
− x1 |
|
+ x |
|
|
= |
|
|
|
|
|||||||||||
|
|
|
|
|
+ |
|
x |
2x |
|
+ |
3x |
4 |
= |
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Нахождение решения представлено на рисунке 5.4. |
|
|
||||||||||||||||||||||
СТ-1 |
3 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
СТ-2 |
|
–1/3 |
4 |
|||
|
↓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↓ |
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
17/3 |
||||||
→ |
–8 |
3 |
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–8/3 |
1/3 |
8 |
||
|
1 |
–10 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–77/3 |
10/3 |
80 |
|
|
|
СТ-3 |
|
|
3/17 |
|
|
|
|
|
–1/17 |
12/17 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
8/17 |
|
|
|
|
|
|
3/17 |
|
168/17 |
|
|
|||||||
|
|
|
|
|
77/17 |
|
|
|
|
|
31/17 |
1668/17 |
|
|
||||||||||
Найденное р шение |
Рис. 5.4 – Поиск решения |
|
|
|
||||||||||||||||||||
x* = |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
по второй переменной не удовле- |
|||||||
творяет усл вию целочисленности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
По второй строке составим дополнительное ограничение (рис. 5.5). |
||||||||||||||||||||||||
Таким образом, получим: |
xɶ* |
= ( |
|
|
|
|
) |
|
|
f |
* |
= − |
. |
|
|
|||||||||
|
3/17 |
–1/17 |
12/17 |
|
1 |
|
–1/3 |
|
1 |
|
8/17 |
3/17 |
168/17 |
|
0 |
|
1 |
|
9 |
|
–8/17 |
–3/17 |
–15/17 |
|
8/3 |
|
–17/3 |
15/3 |
|
|
77/17 |
31/17 |
1668/17 |
|
–1/3 |
|
31/3 |
|
89 |
|
1 |
–1/3 |
1 |
|
|
|
|
|
|
|
0 |
1 |
9 |
|
|
|
|
|
|
|
–8/3 |
–43/9 |
7/3 |
|
|
|
|
|
|
|
1/3 |
92/9 |
268/3 |
|
|
|
|
|
|
|
|
Рис. 5.5 – Учет дополнительных ограничений |
|
|
|||||
······································································· |
|||||||||
5.3 Метод |
и границ |
|
тся на практике для ре |
||||||
|
Методветвейи границ (МВГ) широко |
||||||||
шения как полностью целочисленных задач, использутак смешанных задач целочис- |
|||||||||
ленного линейного программирования (ЦЛП). Он применяется |
большинстве |
||||||||
коммерческих программ решения ЗЦП. По существу МВГ |
редставляет собой |
||||||||
эффективную процедуру перебора всех целочисленных допустимых решений |
|||||||||
[1]. |
Как известно, в методе Гомори решение основано на отсечении |
||||||||
численных допустимых решений. В МВГ используется округление нецелочис- |
|||||||||
ленного оптимального решения ЗЛП. |
Пример 5.4 |
······················· |
|||||||
······················· |
|
||||||||
|
Пусть оптимальное решение двумерной ЗЛП есть |
x* = |
|
) . В каче |
|||||
стве кандидатов на роль приближенного целочисленного оптимального реше- |
|||||||||
ния необходимо рассматривать решения (3;4), (4;4), (4;5), (3;5), полученные |
|||||||||
в результате |
. Истинное оптимальное |
численное решение может |
|||||||
не совпадатьокругленияс одним из четырех, поскольку целое значение |
|
в оптималь- |
|||||||
|
|
|
|
|
|
|
|
|
|
155 |
|
|
|
|
|
|
|
|
|
||
ном реше ии может быть > 4 или < 3. Таким бразом, для получения истинного |
|||||||||||||||||||||
оптимального |
|
|
|
решения |
приходится расс атривать все возмож |
||||||||||||||||
ные значения |
xцелочисленногобольшие меньшие 3,5. Другими словами, |
оптимально цело |
|||||||||||||||||||
численное значение |
x должно удовлетворять неравенству x ≤ |
3 либо |
неравен- |
||||||||||||||||||
ству x ≥ 4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
– либо |
x ≤ 4 |
, либо x |
≥ 5. При |
|
. Аналогично по переменной |
|
|
|
||||||||||||||||||
наличии |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
задаче ЦЛП большого количества переменных важно иметь проце- |
|||||||||||||||||||||
дуру, позволяющую систематически перебирать все возможные целочисленные |
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
реш ния, |
олучаемые при округлении оптимального решения ЗЛП. МВГ по |
||||||||||||||||||||
существу представляет собой такую процедуру эффективного перебора цело- |
|||||||||||||||||||||
числен-ных решений, получаемых при округлении оптимального решения. |
|||||||||||||||||||||
······································································· |
|||||||||||||||||||||
Для иллюстрации основных принципов МВГ рассмотрим следующую за- |
|||||||||||||||||||||
дачу ЦП. |
|
|
|
|
|
|
|
|
|
Пример 5.5 |
······················· |
||||||||||
······················· |
f (x) = 3x |
|
|||||||||||||||||||
Решить задачу: |
|
|
+ |
2x |
|
|
→ max, |
|
|
|
|
||||||||||
|
|
|
|
|
x |
|
≤ |
2; x |
|
≤ |
|
2; |
|
|
|
|
|
||||
|
|
|
|
|
x |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
(5.3) |
||
|
|
|
|
|
+ |
|
|
≤ 3,5; |
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
≥ 0; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x1 |
,x2 |
. |
|
|
|
|
|
|||||||
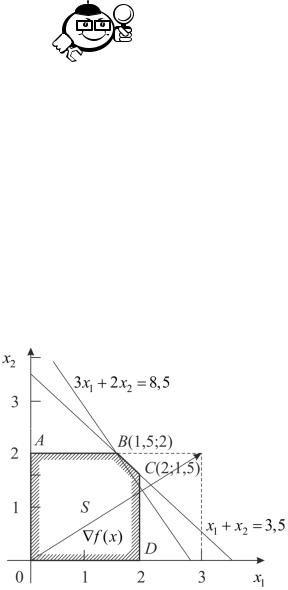
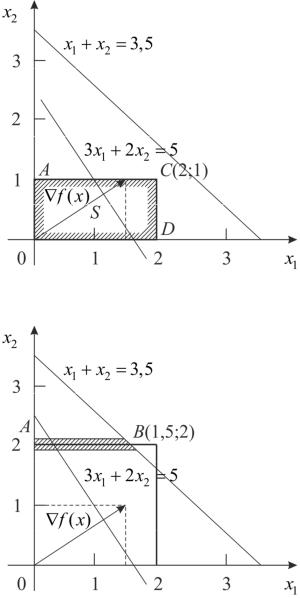
Начальный шаг решения этой задачи состоит в нахождении решения ЗЛП |
|||||||||||||||||||||
без учета целочисленности |
x |
x |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
. На рисунке 5.6 представлено графическое |
||||||||||||||||||||
решение ЗЛП. Оптимальное |
решение1 2 |
|
задачи (5.3) имеет вид: |
x* |
= (2;1,5); f * = 9 . |
||||||||||||||||
Так как x = |
|
|
, то найденное решение не может быть оптимальным ре- |
|||||||||||||||||||||||||||||
шением исходной2 |
задачи ЦЛП. Но найденное значение |
f * = |
представляет со |
|
||||||||||||||||||||||||||||
б й верхнюю границу истинного оптимального решения, поскольку при вы |
|
|||||||||||||||||||||||||||||||
полнении требования целочисленности |
|
значение |
может лишь умень- |
|||||||||||||||||||||||||||||
шиться. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
Следующий шаг МВГ состоит в просмотре це оч сленных значений |
|
|||||||||||||||||||||||||||||||
больших или меньших |
. Это делается путем добавлен я к задаче (5.3) нового |
|||||||||||||||||||||||||||||||
ограничения: либо x |
2 |
≤1,5 |
либо |
|
|
x |
2 |
|
≥ |
|
. Таким образом, |
из задачи (5.3) получа- |
||||||||||||||||||||
ются 2 задачи следующего вида: |
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
f |
|
( |
x |
) |
|
= |
|
|
|
|
+ |
→ |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
≤ |
|
2; x |
|
|
|
|
≤ 2; |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
≤ |
|
1 |
|
|
|
|
2 |
3,5; |
|
|
|
|
(5.4) |
|||||||||||
|
|
|
|
|
|
2 + x |
2 |
|
≤ |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 |
, x2 |
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
x1 |
|
≥ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
. |
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
f1 |
|
|
x2 |
= |
|
|
|
x |
|
+ |
→ |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
( |
|
|
) |
|
|
x |
|
|
|
|
1 |
2; |
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
≥2; |
|
|
|
2 |
3,5; |
|
|
|
|
(5.5) |
||||||||||||||
|
|
|
|
|
|
2 |
+ x |
2 |
≤ |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x1 |
|
|
|
|
|
|
≥ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
, x2 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
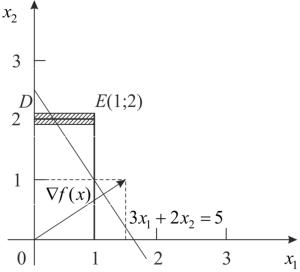
На рисунках 5.7 и 5.8 изображены допустимые области задач (5.4) и (5.5) |
||||||||||||||||||||||||||||||||
соответственно (на рис. 5.8 |
|
|
|
|
≡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
). Допустимые области задач обла- |
||||||||||||
дают следующими свойствами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
) недопу- |
||||||||||||
1. |
Оптимальное решение задачи рисунка 5.6 – (x = |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
стимы для обеих задач (рис. 5.7, 5.8). Таким образом, это решение не |
|||||||||||||||||||||||||||||||
2. |
повт рится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
решение исходной задачи допу |
|
||||||
Любое целочисленное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
стимо и для рисунков 5.8(допустимое)5.9. Таким образом, при введении этих за |
|
||||||||||||||||||||||||||||||
|
дач не происходит потери допустимых целочисленных решений ис- |
|||||||||||||||||||||||||||||||
|
ходной задачи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, т. е. x* = ( |
|
|
||||
Оптимальное решение задачи (рис. 5.7) – это точка |
) |
|
||||||||||||||||||||||||||||||
* = . Таким образом, получено допустимое (целочисленное) решение исход-
|
157 |
* |
целочисленные решения, |
ной задачи ЦП. Даже если задача (5.4) имеет |
|||
значение ЦФ в них не может быть больше 8, т.другие. F = 8 – нижняя гр ница мак |
|||
симального значения F |
ля исходной задачи ЦЛП. Другими словами, опти |
||
мальное значение F исходной задачи не может быть < 8. А так решениекак ран е получена лишь верхняя граница, равная 9, то нельзя утверждать,ходимочто задачи оптимально для исходной задачи. Следовательно, необ также рассмотреть задачу на рисунке 5.8.
Оптимальное решение задачи (рис. 5.8) x =1,5; x |
= 2; F* = 8,5. |
|||
Для исходной задачи это недопустимо, так как |
x |
2 |
принимает дробное зна- |
|
1 |
|
|
. Поэтому необхо- |
|
чение. Оптимальное решение F* = 8,5 > 8 (нижней границы)1 |
||||
|
158 |
S |
|
димо проверить существование в допустимой области |
|
||
решения, дающего значение ЦФ F ≥ 8. Для этого рассмотримЛП−3 целочисленногоЛП-4 |
|||
ЛП-5, получающиеся при добавлении к ЛП-3 |
й x |
≤1задачиx ≥ 2 соот- |
|
ветственно. SЛП−4 |
из отрезка DE (рис.ограничени5.9), задача ЛП-5 не имеет до- |
||
пустимых решений,состоит. е. SЛП−5 = . |
1 |
1 |
|
|
|
||
Оптимальное решение ЛП-4 |
x* = (1;2); F* = 7 . |
значение |
||
Следовательно, для любого целочисленного решения в S |
||||
ЦФ ≤ 7. Таким образом, точка x* = (2;1) задачи ЛП-2 представляетЛП−собой4 |
опти- |
|||
мальное целочисленное решение исходной задачи; оптимальное значение ЦФ |
||||
в этой точке равно 8. |
льность задач ЛП, возникающих при ис- |
|||
Удобно представить |
||||
пользовании процедуры МВГпоследоватвиде дерева |
. 5.10). |
|
ей. |
|
Дерево состоит из множества вершин(риссоединяющих их дуг или |
||||
Вершина 1 соответствует ЛП-1 без учета требований ц |
. Ветвле- |
|||
ние в вершине 1, определяемое целочисленной переменнойелочисленностиx |
|
|
||
ограничения x2 ≤1, приводит к вершине 2 (ЛП-2). Так как ЛП-2 имеетпомощьюпти- |
||||
мальное целочисленное решение, то нет необходимости производить ветвление |
||||
в вершине 2. Такая вершина называется прозондированной. |
|
|
||
Ветвление в вершине 1 по ограничению |
x ≥ 2 дает ЛП-3. Так как опти |
|||
мальное решение ЛП-3 дробное, |
происходит |
2дальнейшее |
|
|
шине 3 по переменной x1. Это приводит к появлению вершин ветвление4 5. Эти верши-
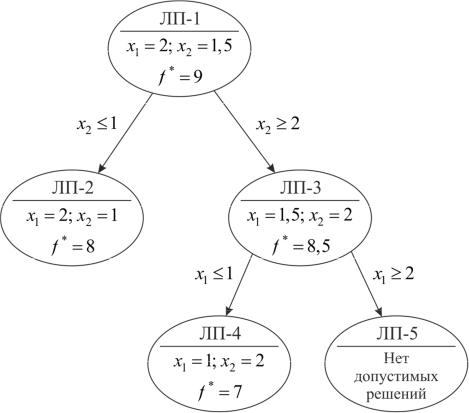
решением, ЛП-5 не имеет допустимых решений.
ны прозондированы, поскольку ЛП-4159обладает оптимальным целочисленным
Наилучшее решение в прозондированных вершинах и есть оптимальное решение исходной задачи.
······································································· |
|||||
Алгоритм МВГ |
|
|
|
|
|
Рассмотрим частично целочисленную задачу вида [1] |
|
||||
|
F |
= cT x |
→ max, |
|
|
|
Ax = b, |
x ≥ 0, |
|
||
|
x |
|
( j I ), |
|
|
где I – множество индексов целочисленных переменных. |
|
||||
|
|
j |
|
|
|
Шаг 1. На первом шаге шается задача ЛП-1, где все ее переменные рас |
|||||
сматриваются как непрерывные. Пусть в оптимальном решении F |
ЛП-1 неко |
||||
торые целочисленные переменные принимают дробные значения,1 |
тогда опти |
||||
мальное решение исходной задачи не совпадает с F . В этом случае F пред- |
|||||
|
|
|
|
1 |
1 |

ставляет собой верхнюю границу оптимального значения |
исходной задачи |
||||||||||||||||||||||
ЛП-1.Шаг 2. Производится ветвление по одной из целочисленных перем нных, |
|||||||||||||||||||||||
имеющей дробное значение |
оптимальном решении ЛП-1. Для |
определения |
|||||||||||||||||||||
пере |
|
енной, по которой |
производится ветвление, разработан ряд правил. При- |
||||||||||||||||||||
ведем некоторые из них. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1. |
Выбор целочисленной переменной, знач ние которой в оптимальном |
||||||||||||||||||||
|
|
2. |
решении ЛП-1 имеет наибольшее дробное значение. |
|
|
|
|
||||||||||||||||
|
|
Приписыва ие целочисленным переменным приоритетов и ветвление |
|||||||||||||||||||||
|
|
|
|
|
по |
переменной |
с наибольшим приоритет м, например: |
|
|
||||||||||||||
|
|
|
|
|
а) |
данная переменная представляет собой важное решение, принима- |
|||||||||||||||||
|
|
|
|
|
б) |
мое в рамках рассматриваемой модели; |
|
|
|
|
|||||||||||||
|
|
|
|
|
ее коэффициент стоимости или прибыли в ЦФ существенно пре- |
||||||||||||||||||
|
|
|
|
|
в) |
восходит остальны ; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
значение данной переменной играет ключевую роль для модели с |
||||||||||||||||||
|
|
|
|
|
|
точки зрения разработчиков и пользователей. |
|
|
|
|
|||||||||||||
|
|
|
3. Произвольные правила выбора. Например, можно выбирать перемен- |
||||||||||||||||||||
|
|
|
|
|
ную с наименьшим н мером. |
|
|
|
|
|
|
|
|
|
, дробное |
||||||||
|
|
|
Пусть |
|
|
|
происходит по целочисленной переменной |
|
|||||||||||||||
значение которойветвление |
|
|
|
решении ЛП-1 равно β . Далее рассматрива- |
|||||||||||||||||||
ются две новые задачиоптимальномЛП-2 ЛП-3, получаемые путем введения ограничений |
|||||||||||||||||||||||
x |
≤ |
|
β |
и x |
≥ |
|
β , соответственно, где |
|
β |
|
– наименьшее целое ≤ |
; здесь |
|||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
– |
целое |
|
значение переменной ; |
|
|
|
– наибольшее целое |
> |
. |
|
||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
β |
|
|
|
||||||||||||||||||
|
|
|
Условия ЛП-2 |
и |
|
ЛП-3 |
можно |
|
|
записать следующим образом (см. |
|||||||||||||
рис. 5.11): |
|
|
ЛП-2 |
|
|
|
|
|
|
|
ЛП-3 |
|
|
|
|
||||||||
|
|
|
|
|
|
F = cT x → |
|
|
|
|
|
|
|
F = cT x → |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Ax = b x |
≤ |
β |
|
|
|
|
|
Ax = b x ≥ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|||||||||
|
|
|
Допустим, что оптимальные решения задач ЛП-2 и ЛП- |
|
3 также содержат |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
дробные значения целочисленных переменных и поэтому не являются допу- |
|||||||||||||||||||||||
стимыми для исходной задачи. |
|
|
|
|
|
≥ |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
≥ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
