
Исследование операций и методы оптимизации
..pdf
|
Наихудшей |
|
|
|
|
|
является вершина |
, поскольку значение функции |
||||||||||||||||||
в этой точке максимальновершиной |
равно 10,432. |
|
|
|
|
|
|
|
||||||||||||||||||
|
Вычислим координаты новой вершины: |
|
|
|
|
|||||||||||||||||||||
|
xɶ2 = |
2 |
|
|
|
n |
|
x j |
− x2 |
|
− x2 |
= ( |
) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Значение фу кции |
n |
этойj=0 |
|
точке |
равно 0,147. Точка не является наихуд- |
||||||||||||||||||||
шей. Эта точка становится |
точкой . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Условие останова не выполняется: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
f |
(x |
0 )− f |
(x1 ) |
|
= |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
f |
|
x1 |
− f |
x2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
f |
|
(x2 ) |
− f (x |
0 ) |
|
|
|
= |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Наихудшей |
|
|
|
|
|
является вершина |
, поскольку значение функции |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
в этой точке максимальновершиной |
равно 3,879. |
) |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
( |
|
|
) |
|
( |
|
|
|
|
|
|
|
|
|
|||
|
Вычислим координаты новой вершины: |
|
|
|
|
|||||||||||||||||||||
|
xɶ1 = |
|
2 |
|
|
|
n |
|
x j |
− x1 |
|
− x1 |
= |
( |
|
) |
ɶ оказалась «хуже» |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Значение функции вn |
этойj=0 |
|
точке |
равно 2,975. Т чка |
|||||||||||||||||||||
всех |
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
точек симплекса, осуществляется возврат к исходному сим- |
||||||||||||||||||||||||||
плексуостальныхпоследующим его сжатием относительно «лучшей» из вершин – |
: |
|||||||||||||||||||||||||
|
ɶ0 |
|
|
|
k + ( |
2 |
− γ) s |
|
|
|
|
|
0 |
|
|
|
|
|||||||||
|
ɶs = γ |
|
|
= |
|
|
≠ |
|
|
|||||||||||||||||
|
x |
|
|
= |
|
|
|
|
x |
|
2 |
+ ( − )x |
1 |
= |
|
|
|
|||||||||
|
ɶ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
): |
|
|
Значения функции в новых точках равно (f (x2 )= |
|
||||||||||||||||||||||||
|
x |
|
|
= |
|
|
|
|
x |
|
+ ( |
− |
= |
)x |
= |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
xɶ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
( xɶ1) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
Выполним проверку критерия останова: |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
f (x0 )− f (x1 ) |
|
|
= 0,586; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
f (x1 )− f (x2 ) |
|
|
|
= 0,281; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
f (x2 )− f (x |
0 ) |
|
|
|
= 0,867. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x1 − x0 |
|
|
|
= |
( |
|
4,001− 4,708)2 |
|
+ (6,123 − 5,415)2 |
=1. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Условие |
|
|
|
останова |
|
|
|
выполняется, т. к. полученные значения меньше ε |
и ε |
2 |
. |
||||||||||||||
|
|
|
|
||||||||||||||||||||||
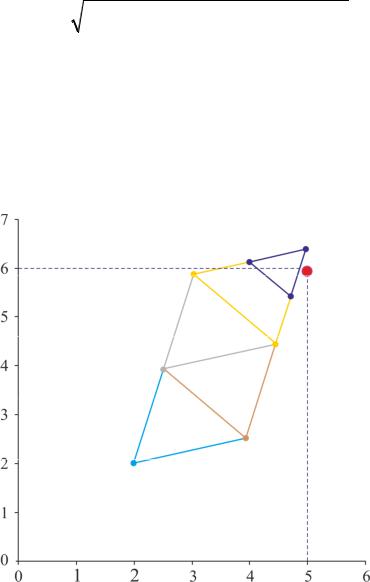
В качестве решения примем точку |
|
|
|
|
|
|
|
4,967 |
|
|
1 |
|
|
||||||||||||
x2 = |
6,381 |
, в которой функция ми- |
|||||||||||||||||||||||
нимальна равна |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
На рисунке 2.0,147представлено перемещение симплекса к точке минимума.
·······································································
2.1.3 Метод Хука – Дживса
Процедура Хука – Дживса представляет собой комбинацию двух поисков [2]:
1) исследующий поиск (для выявления характера локального поведения ческимЦФ определения направления движения вдоль «оврагов») с цикли-
изменением переменных;

|
2) ускоряющий поиск по образцу с использованием определенных эври- |
|||||||||||||||||||||||||||||
|
стических правил. |
|
|
|
|
|
|
|
|
|
|
|
|
. Задается |
||||||||||||||||
|
Исследующий поиск. Выбирается некоторая исходная точка |
|||||||||||||||||||||||||||||
величина шага |
∆ |
, которая может быть различной для разных координатных |
||||||||||||||||||||||||||||
направлений |
изменяться в процессе поиска. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Если значение ЦФ |
|
|
|
пробной точке |
еньше значения ЦФ в исходной точ- |
||||||||||||||||||||||||
ке, то шаг поиска успеш ый. В |
|
противном |
|
случае из исходной точки делается |
||||||||||||||||||||||||||
шаг в противоположном направлении. После перебора всех |
координат иссле- |
|||||||||||||||||||||||||||||
дующий поиск завершается. Полученная точка называется базовой. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Поиск по образцу. |
|
|
|
|
|
|
|
|
|
|
|
|
шаг из |
базовой точки |
|||||||||||||||
вдоль прямой, соединяющейОсуществляетсяэту точку предыдущейполученнойбазов . Новая точка об- |
||||||||||||||||||||||||||||||
разца определяется по формуле: |
|
= xk + xk − xk− |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Как только |
|
|
|
|
|
|
|
|
xk+ |
|
|
нию ЦФ, точка |
|||||||||||||||||
|
|
|
|
|
|
|
|
по образцу не приводит |
||||||||||||||||||||||
следующий поиск.движениеЕсли результате получается точка с меньшим значением |
||||||||||||||||||||||||||||||
|
фиксируется |
|
|
|
|
|
|
|
|
|
|
p |
|
|
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
качестве временной базовой точкиуменьшеи внов проводится ис- |
|||||||||||||||||||||||||||
ЦФ, чем в точке |
|
|
, то о |
|
|
|
|
рассматривается как новая базовая точка |
|
|
|
. Но |
||||||||||||||||||
если исследующий |
|
|
неудачен, то следует вернуться точку |
|
провести |
|||||||||||||||||||||||||
+ |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
исследующий поискпоискцелью выявления нового |
ия минимизации |
|||||||||||||||||||||||||||||
конечном итоге возникает ситуация, когда такой поискнаправлен |
|
|
к успеху. |
|||||||||||||||||||||||||||
В этом случае уменьшается шаг путем введения коэффициентаприводитα возобнов- |
||||||||||||||||||||||||||||||
ляется исследующий поиск. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Схема алгоритма Хука – Дживса |
|
k |
|
– текущая базовая точка; |
|
|
|
– |
||||||||||||||||||||||
|
Введем следующие обозначения: |
|
|
− |
||||||||||||||||||||||||||
предыдущая базовая точка; xp |
|
– точка, построенная при движении по образ- |
||||||||||||||||||||||||||||
цу; |
|
|
|
|
|
|
|
|
|
|
|
k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k +1 – следующая (новая) базовая точка [2]. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Критерий останова: |
|
|
|
|
∆x |
|
|
≤ ε. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Шаг 1. Определить |
|
|
|
начальную точку |
|
; прир щения (ш ги) |
∆ |
i |
= |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
коэффициент уменьшения шага |
α > ; параметр окончания поиска ε . |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2. Провести |
|
|
|
|
|
|
|
|
|
поиск. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Шаг 3. Был ли исследующийпоиск удачным (найдена ли точка с мень- |
|||||||||||||||||||||||||||||
шим значением ЦФ)? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Да: переход на шаг 5. Нет: продолжить, т. е. переход на шаг 4. |
неравенство |
|||||||||||||||||||
|
|
|
|
|
Шаг 4. Проверка на |
|
|
|
поиска. Выполняется |
ли |
|||||||||||||||
|
|
|
|
∆x |
≤ ε? Да: окончание поиска,окончаниет. . текущая точка аппроксимирует точку экс- |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
тремума . |
|
|
|
|
|
|
|
|
|
|
. Переход на шаг 2. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
Нет: уменьшить приращение |
∆ |
α |
|
= |
|
|
|
|||||||||||||
|
|
|
|
|
Шаг 5. Провести поиск по образцу: |
xp |
|
= x + (x |
|
− x |
|
) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k+ |
|
|
k |
|
k |
|
|
k− |
|
xp |
|
в качестве |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Шаг 6. Провести исследующий поиск, используя точку |
|
|||||||||||||||||||
временной базовой точки. Пусть результате получена точка |
|
|
k +1 |
|
|||||||||||||||||||||
|
|
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
Шаг 7. Выполняется ли неравенство: |
|
( |
+1 )< |
|
( |
|
)? |
|
|
|
|
|
||||||||
|
|
|
|
|
Да: положить |
− = |
; |
= |
+ |
. Переход на шаг 5. |
|
|
|
− |
|
|
|
||||||||
|
|
|
|
|
Нет: переход на шаг 4. |
|
|
|
Пример 2.3 |
······················· |
|||||||||||||||
······················· |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
Найти точку минимума ЦФ (рис. 2.5): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
( |
) = |
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.5 – |
|
− . |
( ) = |
+ |
+ |
||
Начальная точка: x0 = − |
|
|
|
||||||
Решение. Зададим следующие величины: |
|
|
|||||||
• |
∆x = |
|
|
– векторная величина приращения шага; |
|||||
|
|
|
|
|
[ |
] |
|
|
|
• |
α = |
|
– коэффициент уменьшения шага ∆ |
; |
|
||||
• |
ε = |
[ |
– параметр окончания поиска. |
|
|
||||
|
|
] |
|
|
|
|
|
|
|
−
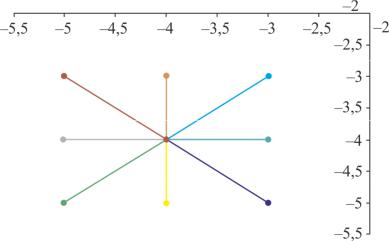
Итерации начинаются с исследующего45 поиска вокруг точки x0 , которой
соответствует значение ЦФ f (x0 )= 272 (рис. 2.6).
Рис. 2. |
|
|
|
|
|
|
x |
|
= −4, дадим приращение |
вычисление |
|||||||||||||||
Фиксируя переменную |
|
x : |
|
||||||||||||||||||||||
|
|
x |
|
|
|
|
|
2 |
(−3;−4) = 200 < f x0 |
|
|
|
|
|
1 |
|
|||||||||
|
|
= −4 +1 → f |
|
|
→ успех. |
|
|||||||||||||||||||
Далее, фиксируем |
x |
= −3 |
и дадим приращение |
|
x |
|
: |
|
|
||||||||||||||||
|
|
1 |
|
= −4 +1 → f (−3; |
−3) = 153 |
( |
|
) |
|
|
|
|
|
||||||||||||
|
|
x |
|
< 200 → успех. |
|
||||||||||||||||||||
Таким |
образом, |
в |
1 |
результате |
исследующего |
2 |
поиска |
найдена точка |
|||||||||||||||||
|
|||||||||||||||||||||||||
x1 = [−3;−3]T |
|
|
2 |
|
|
|
|
|
|
|
|
f |
|
x1 |
|
=153. |
|
|
|
|
|
|
|
|
|
, в которой значение ЦФ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Так как исследующий поиск был удачным, переходим к поиску по образ- |
|||||||||||||||||||||||||
цу (рис. 2.7): |
|
|
|
|
|
xp = x |
|
+ (x |
|
( |
) |
|
|
|
|
; |
|
|
|
|
|||||
|
|
|
|
|
|
|
− x |
) |
= [−2;−2] |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
1 |
f |
1 |
|
|
0 |
|
|
|
T |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
(xp )= 68. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
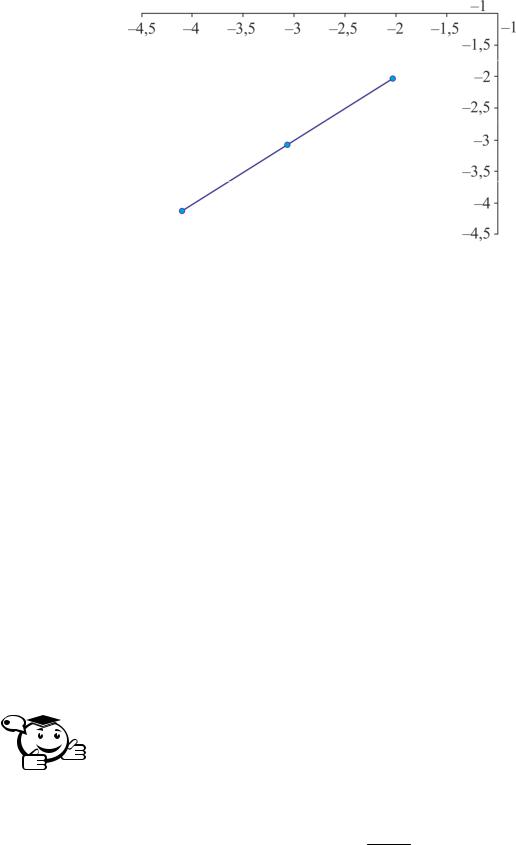
Далее проводится исследующий поиск вокруг точки xp . В результате по- |
|||||||||||||||||||||||||
лучаем точку x2 |
= [−1;−1]T |
, в которой значение ЦФ |
f |
|
|
|
2 |
|
|||||||||||||||||
(x2 )= 17 . |
|
||||||||||||||||||||||||
Поскольку |
f |
|
x2 |
< |
f |
x1 |
, поиск по образцу следует считать успешным и |
||||||||||||||||||
x2 станов тся новой( базовой) ( |
точкой.) |
Итерации продолжаются до тех пор, пока |
|||||||||||||||||||||||
уменьшение |
величины шага не укажет на окончание поиска в |
ε -окрестности |
|||||||||||||||||||||||
точки минимума |
x = [0; 0]T . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
46
|
|
Рис. 2.7 – Поиск |
|
|
|
|
|
|
|
направлении |
||
|
|
|
наилучшего |
|
|
|
|
|
|
|
[–2;–2]) |
|
······································································· |
||||||||||||
|
|
Достоинства метода Хука – Дживса: несложная стратегия поиска, про |
||||||||||
стота вычислений, малый объем требуемой памяти (меньше чем в симплекс- |
||||||||||||
методе). |
|
|
|
|
|
|
|
|
|
|||
|
|
Недо татки: при наличии значительных нелинейных эффектов процесс |
||||||||||
вырождается в |
|
исследующих поисков без перехода к уско- |
||||||||||
ряющему поискупоследовательностьобразцу. |
|
|
|
|
|
|
|
|
|
|||
|
|
Возможные варианты модификации метода Хука – Дживса: |
увели |
|||||||||
|
|
а) |
если дв жение по образцу приводит к успеху, то желате |
|||||||||
|
|
|
чить длину шага по образцу, чтобы полностью использоватльновозмож- |
|||||||||
|
|
б) |
ность поиска вдоль прямой; |
|
|
|
|
|
|
|
||
|
|
введение |
|
правил увеличения и уменьшения прира- |
||||||||
|
|
|
щения переменныхдополнительныхдр. |
|
|
|
|
|
|
|
|
|
2.2 Градиентные методы |
|
|
|
|
|
|
|
|
|
|||
|
|
|
····························································· |
|||||||||
|
|
|
Градиент функции |
f (x) |
многих |
переменных |
некоторой |
|||||
|
|
|
точке x – это |
координатами которого являются частные |
||||||||
|
|
|
производные функциивектор, |
этой точке: |
|
∂f (x) |
|
|||||
|
|
|
|
|
|
∂f (x) |
|
∂f (x) |
|
|
||
|
|
|
f (x) |
= |
∂x |
, |
∂x |
,..., ∂x |
. |
|
||
|
|
|
|
|
|
1 |
2 |
|
n |
|
|
|
|
|
|
······································· ···· ·················· |
|||||||||
|
|
В малой окрестности точки |
x градиент указывает направление наиско |
|||||||||
рейшего возрастания функции, а его норма характеризует скорость этого воз-

|
|
|
|
|
. Вектор-антиградиент указывает направление наискорейшего убыва- |
|||||||||||||||||||||||||||||||||||||||
растанияфункции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-антиградиент |
|||||||||||
|
|
|
В любой точке поверхности целевой функции |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
перпендикулярен касательной к линии уровня |
|
|
|
|
= |
|
|
|
|
|
векторэтой точке. |
|||||||||||||||||||||||||||||||||
|
|
|
Норма вектора-градиента: |
2 |
|
|
|
f x |
2 |
|
|
|
|
|
|
f |
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
f x |
|
|
|
f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
∂ |
|
|
|
∂ |
|
|
|
+ |
|
∂ |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
+ |
|
∂x |
2 |
|
+ |
|
|
|
|
∂x |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||||||||||
|
|
|
В точке, где имеет место экстремум функции, вектор-градиент и все его |
|||||||||||||||||||||||||||||||||||||||||
компоненты обращаются в ноль: |
f ′ |
(x* ) |
= |
( |
|
|
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
····························································· |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Матрица Гессе функции |
|
|
|
|
|
|
многих переменных – это |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
матрица вторых производных: |
|
|
|
|
|
2 |
|
|
|
|
|
... |
|
|
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
2 |
1∂ |
1 |
|
|
∂ |
1∂ 2 |
|
|
|
∂ |
1∂ |
n |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
H x = 2 f x |
|
|
|
|
|
∂ |
|
|
∂ |
|
|
... |
|
∂ |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
2 |
|
|
|
|
|
|
∂ |
2 |
|
|
|
|
|
|
∂ |
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
2∂ |
1 |
|
|
∂ |
2∂ 2 |
|
|
|
∂ |
2∂ |
n |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
∂2 |
... |
|
|
|
... |
|
∂2 |
... |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 |
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
n |
∂ |
1 |
|
|
∂ |
n |
∂ |
2 |
|
|
|
∂ |
n |
∂ |
n |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
············································· ····· ··········· |
|||||||||||||||||||||||||||||||||||||
|
|
|
Предполагается, что целевая функция |
f |
(x) |
непрерывна и имеет по край |
||||||||||||||||||||||||||||||||||||||
ней мере непрерывные первые производные. Необходимым условием суще |
||||||||||||||||||||||||||||||||||||||||||||
ствования экстремума является наличие стационарной точки ЦФ. Таким обра |
||||||||||||||||||||||||||||||||||||||||||||
зом, основная идея многих методов оптимизации без ограничений в простран- |
||||||||||||||||||||||||||||||||||||||||||||
стве |
|
|
заключается в отыскании стационарной точки |
, в которой градиент |
||||||||||||||||||||||||||||||||||||||||
ЦФ f |
( |
x |
) |
= . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Эта задача эквивалентна решению нелинейной системы уравнений вида: |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ f |
( |
x |
) |
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ xi |
непосредственно этой системы, что приво |
||||||||||||||||||||||||||||||
|
|
|
Можно отыскивать решение |
|||||||||||||||||||||||||||||||||||||||||
дит к методу Ньютона. При этом предполагается, что функция дважды дифференцируема.
|
|
В данном случае речь идет об итерационных процессах, порождающих |
||||||||||||||||||||||
последовательность точек |
0 1 |
… |
|
, сходящихся к локальному экстремуму |
||||||||||||||||||||
функции |
в точке |
|
. |
|
|
|
|
|
определяется выражением: |
|||||||||||||||
|
|
На каждом |
|
|
|
-м этапе значение |
k |
|||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k+1 |
= |
+ λ |
|
|
|
|
||
– направление перемещения, которое может быть: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
• либо градиентом функции в точке |
, т. е. |
k |
= − ( ); |
); |
||||||||||||||||||
|
|
• |
либо вычисленным, исходя из направления градиента ( |
|||||||||||||||||||||
|
|
• |
либо выбранным произвольно при условии, ч |
это будет |
аправление |
|||||||||||||||||||
|
|
|
спуска. |
|
|
|
В |
этом |
случае |
должно |
выполняться неравенство вида: |
|||||||||||||
|
|
|
f |
T |
|
|
|
xk |
|
|
|
d |
|
< . |
|
|
|
|
|
длину шага. |
|
|||
|
|
Здесь |
λ |
|
|
|
– параметр, |
|
|
|
|
|
|
|||||||||||
|
|
Способ определения |
характеризующийλ на каждой итерации связан с особенностями |
|||||||||||||||||||||
|
|
|
|
|
( |
|
|
) |
|
k |
|
|
|
|
|
|
осуществляется путем решения зада- |
|||||||
применяемого метода. Обычно выбор |
λ |
|||||||||||||||||||||||
чи минимизации |
|
|
|
|
( |
) |
направлении |
|
. Поэтому при реализации изучаемых |
|||||||||||||||
методов необходимо |
использовать |
эффективные методы одномерной оптими- |
||||||||||||||||||||||
зации.В семействе градиентных методов следует выделить методы с заданным |
||||||||||||||||||||||||
шагом, в которых заранее задаются значения |
λ . |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
что построенная последовательность сходится к решению, т. е. |
||||||||||||||||
|
→ Доказано,если выполняются два условия: |
|
|
|
|
|
||||||||||||||||||
k |
|
1) |
λk |
→ |
|
|
при |
|
→ ∞; |
, λk = |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2) |
∑λk |
→ +∞ |
|
|
|
|
|
|
|
|||||||||||||
|
|
Данная процедура («метод расходящегося ряда») может оказаться мед- |
||||||||||||||||||||||
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ленной. |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Критерии останова (наиболее употребительные). |
|
|||||||||||||||||||||
|
|
Пусть ε > |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
– заданная точность: |
|
|
|
|
|
|
|||||||||||||
|
|
1) |
|
|
|
|
|
∂f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
i=1,n |
|
x |
|
|
≤ ε |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
2) |
|
f |
2= ∑ |
|
|
≤ ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
n |
|
∂ f 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3) |
|
f (x |
k+1 )− f ( |
xk ) |
≤ ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
i=1 |
|
∂xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4) |
|
f |
= ∑ |
∂ f |
|
|
|
≤ ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
5) |
|
|
|
n |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
∆x |
= xk+1 |
− xk ≤ ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
i=1 |
∂xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2.2.1 Градиентный спуск |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Итерационная формула метода градиентного спуска имеет вид: |
|
|
||||||||||||||||||||||||||||
|
Здесь α |
– параметр спуска (обычно используются значения α = |
|
|
|||||||||||||||||||||||||||
|
|
|
|
). В случае если |
α |
слишком большое, |
озможна ситуация, когда |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
= |
− α |
( |
|
) |
|
|
|
|||||||
метод не будет сходиться (значение функции будет увеличиваться). При малом |
|||||||||||||||||||||||||||||||
значении параметра возможна медленная сходимость. |
······················· |
||||||||||||||||||||||||||||||
······················· |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2.4 |
||||||||||||||||||
+(x |
Методом градиентного спуска найти минимум функции f (x) = (x |
− 5)2 |
+ |
||||||||||||||||||||||||||||
− ) |
. Пусть α = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
2 |
Критерий останова |
|
|
|
xk+1 − xk |
|
|
|
≤ ε , ε = |
|
|
. Начальная точка [10;10]. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Частные производные |
|
|
|
равны: |
|
|
|
x |
x |
|
|
x |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
f |
( |
|
2 ) |
= |
− |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
f |
|
1 |
x |
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
1 |
( |
|
x |
2 ) |
= |
x |
− |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
||||
|
Вычислим координаты но2вой точки по итерационной формуле: |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
= |
|
|
|
|
− α ( |
|
) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
= |
|
− |
|
|
|
|
|
|
|
|
− |
|
|
= |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Проверим условие останова: |
|
2 |
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
x1 |
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
( − |
|
) |
+ ( |
|
− |
|
) |
|
= |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Значение больше 0,3, |
следовательно, переходим к следующей итерации. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
− α |
( |
) |
|
|
|
|
|
|
|||
Проверим условие останова: |
|
|
|
|
− |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
x2 = |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
− |
|
= |
|
|
|
|||||||||||
|
|
|
|
|
|
x2 − x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
= |
|
|||||||||||
|
|
|
|
|
|
|
= |
|
( |
|
− |
) |
+ ( |
|
− |
|
) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Значение превышает |
|
0,3, следовательно, условие останова не выполняется. |
|||||||||||||||||||||||||||||
Вычислим новую точку: |
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
− α |
|
|
|
|
|
|
|||||
Проверим условие останова: |
|
|
|
− |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
− |
|
= |
|
|
|
||||||||||
|
|
|
|
x3 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
= |
|
|
( |
|
|
|
− |
|
|
+ |
|
− |
) |
= |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Значение |
|
|
|
меньше |
|
|
|
0,3, следовательно, работа алгоритма завершается. Ре- |
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
шением задачи является точка (5,04;6,032). |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
······································································· |
|||||||||||||||||||||||||||||||
2.2.2 Метод наискорейшего спуска (метод Коши) |
|
||||||||||||||||||||||||||||||
Известный французский математик Огюстен Луи Коши первым исполь- |
|||||||||||||||||||||||||||||||
зовал аналогичный алгоритм для решения системы линейных уравнений [1]. |
|||||||||||||||||||||||||||||||
В широко |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
методе Коши (МК) |
λ |
выбираются так, чтобы |
||||||||||||
минимизироватьиспользуемомфункцию λ : |
|
|
|
− λ f (x |
|
|
|
|
|
||||||||||||||||||||||
на множестве значений λ ≥ |
g(λ) = f x |
k |
k |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
(одномерная минимизация). |
||||||||||||||||||||||||||||||
Алгоритм Коши |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 Выбрать начальную точку . |
), найти такое λ , что |
||||||||||||||||||||||||||||||
Шаг 2. На |
|
|
-й итерации, где |
k |
= − ( |
||||||||||||||||||||||||||
