
Исследование операций и методы оптимизации
..pdf
|
Выполним |
проверку условия: |
|
|
f |
′(x |
) |
≤ ε |
|
|
f ′(x |
) |
= |
|
|
− = . |
||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
Данное |
|
меньше точности |
ε , |
следовательно, |
выполнение алгоритма за- |
|||||||||||||||
|
|
|
|
|||||||||||||||||
вершаетсязначениев качестве решения принимается точка |
x* = x = |
|
. |
|
||||||||||||||||
1.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
методов одномерной оптимизации |
|
|
|
|||||||||||||||
|
Сравнениепомощью теоретических выкладок можно показать, что такие методы |
|||||||||||||||||||
точечн го оценивания, как метод Пауэлла, метод поиска с использованием |
||||||||||||||||||||
производных, существенно эффективнее методов исключения интервалов, сре- |
||||||||||||||||||||
ди которых выделяется метод золотого сечения. Данный вывод |
|
|||||||||||||||||||
лишь в предположении, что интервалы сходимости сравнимы междусправедливсобой, |
||||||||||||||||||||
исследуемая функция является достаточно гладкой и унимодальной. Выбор то- |
||||||||||||||||||||
го или иного метода |
пределяется из |
|
|
|
|
|
|
|
соображений [1]: |
|
||||||||||
|
1. |
Если необходимо получить |
следующихрешение очень высокой степенью точно |
|||||||||||||||||
|
|
сти, то лучшими оказываются методы на основе полиномиальной ап- |
||||||||||||||||||
|
2. |
проксимации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Если важно добиться надеж ой работы алгоритма, то целесообразно |
|||||||||||||||||||
|
3. |
выбрать м тод золотого сечения (МЗС). |
|
|
|
|
|
использовать сов |
||||||||||||
|
|
|
методы типа метода Пауэлла |
|
|
|||||||||||||||
|
|
Поисковыеместно МЗС, когда возникают затрудненияследуетреализацией соответ- |
||||||||||||||||||
|
|
ствующих итераций на ЭВМ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
стики:Для оценки эффективности методов обычно используются три характери- |
||||||||||||||||||||
|
• |
время, затраченное на получение решения; |
|
|
|
|
|
|||||||||||||
|
• |
точность решения; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
• |
чувствительно ть к изменениям параметра сходимости. |
|
|
||||||||||||||||
|
Например, метод средней точки, метод Пауэлла могут быть исследованы |
|||||||||||||||||||
при поиске минимума функции |
( |
) = sink ( ), |
x |
[ |
|
π] |
для различных не- |
|||||||||||||
четных значений |
: |
] x* = |
|
f |
|
x* |
|
|
|
|
для любого . |
|
|
|||||||
|
|
k [ |
|
( |
) |
= − |
|
|
|
|||||||||||
|
При возрастании значения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
увеличивается время решения и уменьшает- |
|||||||||||||||||||
ся точность. Однако МЗС не чувствителен к росту . |
|
|
|
|
|
|||||||||||||||
|
В |
|
|
отметим, что МЗС обладает высокой вычислительной эф |
||||||||||||||||
фективностьюзаключениепростотой реализации. Методы точечного |
ценивания позво- |
|||||||||||||||||||
ляют определить точки экстремума с помощью квадратичной аппроксимации

целевой функции. |
интервалы сходи |
ости сравнимы между собой, а целе |
||
функция гладкаяЕслиунимодальная, то |
методы точечного ценивания сходят |
|||
ваязначительно быстрее, чем методы исключения интервалов. Однако при ис- |
||||
следовании |
мультимодальных или быстроизменяющихся функций (типа |
|||
( ) = |
|
, которая обладает узкими впадинами вблизи точки минимума) |
||
наиболее надежным оказывается метод золотого сечения. |
||||
|
|
····························································· |
||
|
|
Контрольные вопросы по главе 1 |
||
1 |
|
····························································· |
||
|
|
глобального |
||
2 |
|
точка называется точкой локального минимума? |
||
3 |
|
|
унимодальной? |
|
4 |
|
функция называется выпуклой? |
||
5 |
|
|
тационарной? |
|
6 |
Какая точка называется седловой? |
|||
7 |
|
|
равномерно поиска? |
|
8 |
|
|
дихотомии? |
|
9. |
|
|
Ньютона? |
|
10. |
В чем суть метода средней точки? |
|||

|
|
2 Методы многомерной оптимизации функций |
|||||||||
найтиЗадачи, которые будут рассмотрены в этой части, имеют следующий вид: |
|||||||||||
где f |
x |
|
= f |
x |
x |
…x |
x |
−∞ ∞ |
( ) |
функции для сущ ствова |
|
|
Для выпуклой непрерывно |
|
|||||||||
ния локального минимума необходимодифференцируемойдостаточно лишь |
выполнение равен- |
||||||||||
ства: |
( |
) |
|
( 1 |
2 |
n ) |
i |
( |
) |
|
|
f |
|
x* |
= |
|
|
|
|
|
|
|
|
|
Методы, ориент рованные на решение задач безусловной оптимизации, |
||||||||||
можно условно |
разделить |
на три больших класса: |
|
||||||||
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
• |
|
методы прямого поиска (нулевого порядка), основанные на вычисле- |
||||||||
|
|
|
нии только значений ЦФ; |
|
|
|
|||||
|
• градиентные методы (методы 1-го порядка), в которых используются |
||||||||||
|
|
|
значения первых |
|
|
|
|
|
|||
|
• методы 2-го порядкапроизводных;, которых используются также вторые произ- |
||||||||||
|
|
|
водные целевой функции |
. |
|
эффективно |
|||||
|
Ни один метод или класс методов не |
|
|||||||||
стью при решении оптимизационных задач |
отличаетсятиповысокой. В некоторых си- |
||||||||||
туациях вычисление значений ЦФ ребует чрезмерных затрат времени. Иногда |
|||||||||||
евозможно или очень трудно найти аналитическое выражение для производ |
|||||||||||
ных целевой функции. Поэтому при использовании градиентных методов сле |
|||||||||||
дует применять процедуру разностной аппроксимации производных. Таким об- |
|||||||||||
разом, в каждом конкретном случае необходимо приспосабливать |
|||||||||||
применяемый метод к конкретным характеристикам решаемой ЗО. |
|||||||||||
2.1 Методы прямого поиска |
|
|
|
||||||||
|
Рассмотрим три метода прямого поиска локального минимума: |
||||||||||
|
1 |
|
Метод Гаусса. |
|
|
-метод. |
|
|
|||
|
2 |
|
Поиск по симплексу, или |
|
|
||||||
|
3. |
|
Метод Хука – Дживса. |
|
|
|
|||||
|
Достоинства данных метод в: относительная простота вычислительных |
||||||||||
процедур, легкость реализации и корректировки. |
|
||||||||||
Н достатки: значительные затраты времени по сравнению с градиент- |
|||||||||||||
ными методами. |
|
|
|
|
|
|
|
|
|
|
|
||
2.1.1 Метод Гаусса |
|
|
|
|
|
|
|
|
|
том, что на каждом шаге |
|||
Это простейший алгоритм, |
|
|
|
||||||||||
(каждой итерации) минимиз ция осуществляетзаключающийсятолько по одной компоненте |
|||||||||||||
вектора переменных |
|
(остальные |
равны фиксированным значениям). Таким |
||||||||||
образом, алгоритм сводится |
|
многок атному выполнению процедуры одно- |
|||||||||||
мерной оптимизации. В качестве критериев останова могут быть использованы |
|||||||||||||
следующие условия: |
|
x j − x j−1 |
|
|
|
|
|
f (x j )− f (x j+1 ) |
|
≤ ε |
|
||
|
|
|
|
|
|
|
≤ ε |
|
|
|
|||
|
|
|
|
|
|
|
|||||||
······················· |
|
|
|
|
|
|
|
|
|
Пример 2.1 |
|
······················· |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
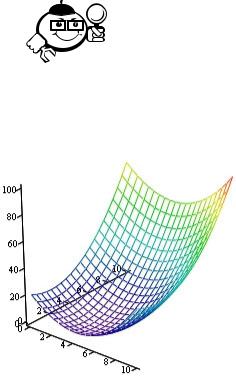
Рассмотрим пример минимизации функции |
|
f (x) = (x − |
) + (x − ) |
||||||||||
(рис. 2.1). |
|
|
|
|
|
|
|
|
1 |
2 |
|||
|
|
|
|
Рис. 2.1 – |
x0 |
( |
) |
= ( |
1 − |
) + (x2 − |
) |
|
|||||
точке |
Пусть начальная точка равна |
= (− |
− |
). Значение функции в этой |
|||||||||||||
|
равно |
f |
x0 |
|
= (− − )2 + |
(− |
− |
)2 |
= |
|
. |
Зафиксировав |
значение |
||||
x |
|
= − |
, определим минимум функции f |
(x |
) = (x |
− |
) + (− |
− ) |
на интер- |
||||||||
вале [ |
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
||
|
]. Используем метод равномерного поиска с шагом 1 (табл. 2.1). |
||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.1 – Равномерный поиск минимума |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
функции |
|
f |
( |
|
x |
|
|
= |
|
x |
|
|
− |
5) |
|
+ |
|
− |
− |
|
7) |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
10 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
1 ) |
|
4( |
1 |
|
|
|
|
|
|
( 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
160 |
|
|
|
153 |
|
|
|
148 |
|
|
|
|
|
|
145 |
|
|
|
|
|
|
|
144 |
|
|
145 |
|
|
|
148 |
|
153 |
|
|
|
160 |
|
|
|
169 |
|
180 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
Из |
|
таблицы 2.1 |
|
видно, |
|
|
|
что |
|
минимальное |
|
значение функци |
|
|
|
наблюдается |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в точке |
|
x |
|
= |
. Зафиксируем полученное значение |
, найдем |
значение |
, при |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
котором минимальна функция |
|
f |
(x |
|
) = ( |
|
− |
|
|
) |
|
+ (x − |
) |
(табл. 2.2). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.2 – Равномерный поиск минимума |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
функции |
f |
( |
|
|
|
x |
|
|
|
|
= |
|
|
|
− |
5 ) |
+ |
|
x − |
|
)7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
10 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 )4 ( |
|
|
|
|
|
|
|
|
(62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
16 |
|
|
25 |
|
|
|
36 |
|
|
|
|
49 |
|
64 |
|
|
|
|
|||||||||||
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Минимум |
|
функции |
|
находится |
|
в точке |
|
x |
|
|
|
|
|
. Таким |
|
образом, |
|
полученная |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
точка |
|
|
|
|
= |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x1 |
= |
|
|
|
|
, значение |
|
|
|
функции |
|
в |
|
этой |
|
2точке |
равно 0: |
f x |
= |
|
4 |
− 4 |
|
2 + |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+( |
|
Поверим условие останова |
|
|
|
|
f |
(x j )− f |
(x j+1 ) ≤ ε |
(при ε |
2 |
= |
( |
|
|
): |
|
( |
|
|
|
) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
− |
|
)2 |
|
=( . |
|
) |
|
|
|
|
|
|
|
f |
|
|
|
x0 |
|
|
|
|
f |
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
− |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
начение больше 0,1, следовательно, |
|
условие останова не выполняется. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Зафиксируем точку |
|
x |
|
|
|
|
= |
|
|
найдем минимум функции |
|
f (x |
) = (x |
− 4)2 + |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
) |
|
|
|
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+ |
− |
|
|
|
|
|
|
на интервале |
|
|
|
|
|
|
|
|
|
|
. Полученное значение, так же как |
|
|
|
на предыду- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
щей итерации, равно x = |
|
. Фиксируя это значение, снова получим, что x |
|
= |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и точка |
) |
x |
2 = ( |
|
|
|
|
). |
1 |
[ |
|
|
|
2 |
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|||||||||||||
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Поверим условие останова: |
|
|
x1 |
|
|
− f |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
значение меньше |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
, следовательно, работа алгоритма завершается. В качестве |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
решения принимается точка |
|
|
|
|
x* |
= ( |
|
|
|
|
|
|
|
) |
). |
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
·······································································
2.1.2 Симплексный метод |
36 |
предложен |
в |
1962 г. |
Спендли |
|||||||||||
|
|
|
Метод |
поиска |
|
был |
||||||||||
(W. Spendley), Хекст |
(G. симплексуR. Hext) Химсвортом (F. R. Himsworth). Этот |
|
- |
|||||||||||||
тод называют последовательным симплекс-методом (ПСМ). Следует отметить, |
||||||||||||||||
что указанный метод |
другие подобные методы не имеют отношения к сим- |
|||||||||||||||
плекс-методу |
линейного программирования (ЛП), а сходство названий носит |
|||||||||||||||
чисто случайный характер. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
····························································· |
|||||||||||
|
|
|
|
|
|
|
|
В k -мерном эвкл довом п остранстве k |
-мерный симплекс |
|||||||
|
|
|
|
|
представляет собой |
фигуру, образованную |
k +1 точками (верши- |
|||||||||
|
|
|
|
|
нами), не принадлежащими одновременно ни одному пространству |
|||||||||||
|
|
|
|
|
меньшей размерности [2]. |
|
|
|
|
|
|
|||||
|
|
|
|
|
····························································· |
|||||||||||
|
|
|
В одн мерном пространстве симплекс есть отрезок прямой; в |
.двумер. |
- |
|||||||||||
ном – треугольник; в трехмерном – треугольная пирамида (тетраэдр) |
|
|||||||||||||||
|
|
|
Из любого |
|
отбросив одну |
вершину, можно получить но- |
||||||||||
вый симплекс, еслисимплекса,оставшимся добавить всего лишь одну точку. |
|
|
|
|||||||||||||
|
|
|
|
|
····························································· |
|||||||||||
|
|
|
|
|
|
|
|
Симплекс называется регулярным, если расстояния между |
||||||||
|
|
|
|
|
вершинами равны. В ПСМ используются регулярные симплекс-планы. |
|
||||||||||
|
|
|
Для |
····························································· |
||||||||||||
|
|
|
оценки направления |
движения во всех вершинах симплекса |
V , |
|||||||||||
j =1,2,…,n +1, где n |
– размерность вектора |
x , необходимо оценить значение |
||||||||||||||
ЦФ f |
|
= f |
V |
. |
|
|
|
|
|
|
|
j |
|
|||
j |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
( j ) |
|
|
|
|
|
|
|
|
|
|
||
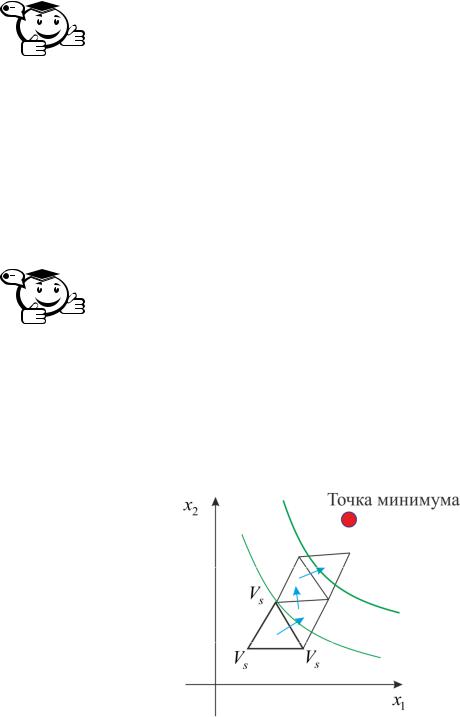
Рис. 2 |
симплексу |

шины |
При поиске минимума наиболее целес образно будет движение от вер- |
|||||||||||||||||||||||||||||||||||
|
|
|
наибольшим значением |
|
|
|
|
|
к противоположной грани симплекса. |
|||||||||||||||||||||||||||
Шаг |
поиска |
|
|
выполняется переходом из некоторого симплекса |
− |
в новый |
||||||||||||||||||||||||||||||
симплекс |
|
|
путем исключения вершины |
|
|
|
|
|
и построения ее зеркального |
|||||||||||||||||||||||||||
отображения относительно общей грани |
|
(рис. 2.2). Многократное отражение |
||||||||||||||||||||||||||||||||||
худших вершин приводит к шаговому движению центра симплекса к цели по |
||||||||||||||||||||||||||||||||||||
траектории некоторой ломаной линии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Алгоритм ПСМ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Шаг 1. Задается исходная вершина симплекса [1]. |
|
. Строится |
||||||||||||||||||||||||||||||||
|
|
Задается коэффициент сжатия |
|
|
γ |
|
и размер симплекса |
|||||||||||||||||||||||||||||
симплекс: |
|
|
|
|
|
|
|
|
|
|
|
= ( |
|
1 |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
... |
|
x |
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x j |
|
= |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
(2.1) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
x |
|
n |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
... |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||||
|
|
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
( j = |
|
n + ), где |
||||
|
|
|
|
-я строка – это координаты |
-й вершины |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n− |
|
|
|
|
|
− |
|
|
|
|
|
|
||||
– размерность пространства (размерность вектора |
|
), |
– номер координаты |
|||||||||||||||||||||||||||||||||
= |
|
. |
|
|
|
|
|
|
|
|
|
, |
начиная со второй, производится по формуле |
|||||||||||||||||||||||
|
|
Определение координат |
|
|
||||||||||||||||||||||||||||||||
где ɶ |
|
|
|
|
|
|
|
|
ij = |
i0 |
+ ɶij |
|
|
( |
|
|
|
|
= |
|
|
|
|
|
|
= |
|
) |
|
|
(2.2) |
|||||
|
– матрица размерности ( |
|
+1) . |
n ... |
|
|
|
|
|
|
(2.3) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ɶj |
|
= |
|
|
|
n |
|
|
|
|
|
|
n |
|
n |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
( i |
) |
|
|
|
|
n |
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
n ... |
|
|
|
|
|
|
|
|||||
где pn = L |
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
n |
|
|
|
|
|||||||||||||||
|
|
( n + + n − ) |
qn |
|
|
|
|
|
|
|
|
( |
n + |
− ) |
|
|
|
|
|
|
||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Векторы, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вершинам |
|
|
|
|
, определяемые формулой |
|||||||||||||||||||||||
(2.2), составят одинаковыесоответствующиеуглы координатными осями |
|
1 |
|
|
. |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
j ) |
|
|
|
|
|
|
Шаг 2. В вершинах симплекса вычисляется ЦФ |
( |
|
|
= |
|
|
|
|||||||||||||||||||||||||||||||||||||
Шаг 3. Проверяем условия: |
|
x j |
− x j−1 |
|
|
|
≤ ε |
|
|
f |
x j |
− f |
x j+1 |
) |
|
≤ ε |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Если «да», то конец; если «нет», то |
|
переходим( |
на)шаг(4. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Шаг 4. |
Н ходится |
«наихудшая» вершина симплекса (при поиске мини- |
||||||||||||||||||||||||||||||||||||||||||
мума «наихудшая» |
вершина – та, в которой значение функции максимально). |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f (xp )= |
|
|
{f |
|
(x j ) |
j = |
|
n + } |
|
|
|
|
|
|
|
|
||||||||||||||||
Шаг 5. Осуществляется расчет координат новой вершины (вершина от- |
||||||||||||||||||||||||||||||||||||||||||||
ражения |
): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Шаг 6. Если точка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точек сим- |
||||||||||||||||
ɶ |
|
|
|
|
|
|
|
|
|
|
|
|
«хуже» всех |
|
|
|
|
|
|
|||||||||||||||||||||||||
плекса, то осуществляется возвратоказываетсяисходному симплексуостальныхпоследующим его |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɶ |
|
n |
|
∑j=0 |
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сжатием относительно «лучшей» из вершин |
|
: |
|
n |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Переход на шаг 2ɶs. |
|
f (xk |
)= |
|
j |
{f |
(x j |
) |
|
j = |
|
} |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
= γ |
k |
+ ( |
− γ) |
s |
|
|
|
= |
|
|
|
|
|
|
|
≠ |
|
|
|
|
|
|
|
|
||||||||||||||||||||
Если |
ɶ |
не является «худшей» в новом симплексе, то перейти на шаг 3. |
|
|||||||||||||||||||||||||||||||||||||||||
······················· |
|
|
|
|
|
|
|
|
Пример 2.2 |
······················· |
||||||||||||||||||||||||||||||||||
Рассмотрим |
пример |
оптимизации |
|
|
функции |
f (x) |
= |
(x |
|
− ) + (x − |
) |
|||||||||||||||||||||||||||||||||
(γ = |
). Минимальное значение функции находится в точке |
( |
1 |
|
) (рис. 22.3). |
|
||||||||||||||||||||||||||||||||||||||
Пусть длина ребра симплекса равна |
|
|
|
|
= |
|
, размерность пространства рав- |
|||||||||||||||||||||||||||||||||||||
на 2, ε |
= |
, |
ε |
|
= |
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
p2 |
|
|
L |
|
|
|
|
n |
|
|
+ n − = |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
= |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ + − = |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
n |
|
|
q = |
|
L( |
|
n +1 |
−1) |
= |
2( |
|
2 +1 |
−1) = |
|
) |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n
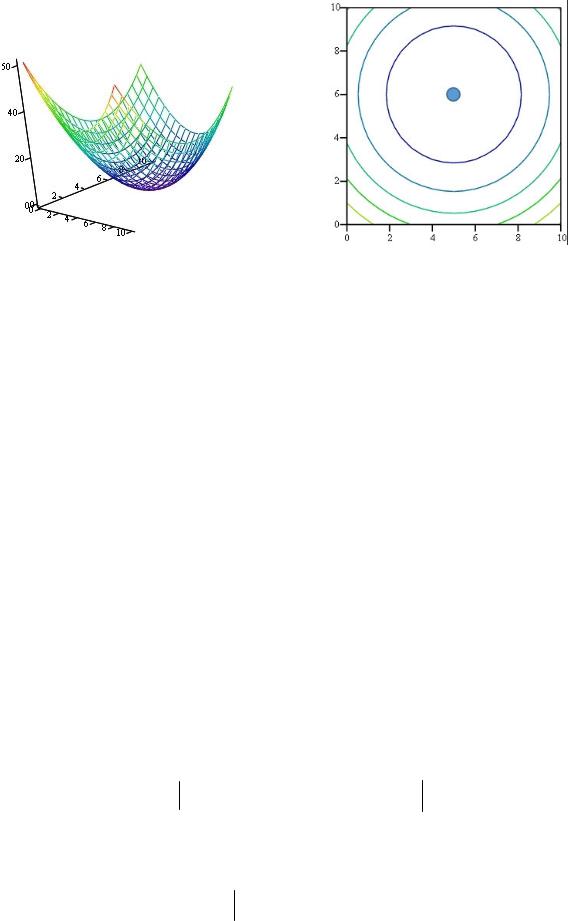
Рис. 2.3 – а) график функции f |
(x) |
= ( |
− |
) |
|
+ ( |
2 |
− |
) |
||||||||||||||||||||||||||||||||||
Матрица ɶ (2.1): |
|
|
|
|
|
б) контурный график 1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
xɶ |
j |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пусть точка x0 = |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
. Тогда матрица |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
x j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
То есть значения матрицы |
|
|
ɶ |
|
|
|
|
(2.3) увеличены на 2 (2.2). |
|
|
|||||||||||||||||||||||||||||||||
В вершинах симплекса вычислим |
ЦФ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
( |
i |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
f |
|
x0 |
|
= f (2,2) = (2 |
− 5)2 + |
(2 |
|
− 6)2 = 25; |
|
|
|
|||||||||||||||||||||||||||||||
f (x1 )= f ( |
( |
|
|
) |
|
|
x j |
|
|
|
) = ( |
≤ ε |
|
|
− |
|
)2 |
+ ( |
|
|
− )2 = |
|
|
||||||||||||||||||||
Проверяем условия: |
|
|
− x j−1 |
, f |
|
x j |
|
|
− f |
|
x j+1 |
|
|
≤ ε . |
|
||||||||||||||||||||||||||||
f (x2 )= f ( |
|
|
|
|
|
|
|
|
|
|
|
) = ( |
|
|
|
|
− |
|
)2 |
|
+ |
( |
|
|
− |
|
)2 |
= |
|
|
|||||||||||||
Разность значений |
|
функции в |
|
|
|
|
|
двух |
|
вершинах симплекса: |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
f |
|
x0 |
|
|
|
− f |
|
|
x1 |
|
|
|
|
|
|
= |
|
− |
( |
|
) |
|
= |
( |
|
|
) |
|
|
|
|
|||||||||
|
f |
x1 |
− f |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
= |
|
|
|
|
− |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
( |
|
|
) |
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(f |
(x)2 )− (f (x)0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
− |
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Расстояние между точками: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
x1 − x0 |
|
|
|
= |
|
|
|
( |
|
|
|
|
|
|
|
− |
)2 + ( |
|
|
− )2 |
= |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
ления.Полученные |
|
|
|
|
значения |
|
|
|
|
превышают |
ε |
|
|
|
|
и ε |
. Поэтому продолжаем вычис- |
||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Наихудшей |
|
|
|
|
|
|
|
|
|
|
|
|
является вершина |
, поскольку значение функции |
|||||||||||||||||||||||||||
в этой точке максимальновершинойравно 25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Вычислим координаты новой вершины: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
xɶ0 = |
2 |
|
|
n |
|
|
x j − x0 |
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− x0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Значение функции в этой точке равно 2,707: |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
∑j=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, точка не является наихудшей. Обозначим её . |
|||||||||||||||||||||||||||||||||||||||||
Условие останова не выполняется: |
)2 + ( |
|
|
|
|
|
|
− )2 = |
|||||||||||||||||||||||||||||||||
f ( |
|
|
|
|
|
|
|
|
|
|
|
|
) |
= |
( |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
f |
x0 |
|
|
− f |
|
|
|
x1 |
|
= |
|
|
|
|
|
− |
|
|
= |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
f |
(x1 ) |
− f |
|
(x |
2 ) |
|
= |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
= |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
f |
(x2) |
− f( |
|
x0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
= |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Наихудшей |
|
вершиной является |
|
вершина |
, |
|
поскольку значение функции |
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
в этой точке максимально |
|
|
|
|
|
равно 13,268. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Вычислим координаты |
новой вершины: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
xɶ1 = |
|
2 |
|
|
|
|
n |
|
|
x j |
− x1 |
|
|
= ( |
|
|
|
|
|
|
|
) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− x1 |
|
|
|
|
|
|
|
||||||||||||||||||||
Значение функции в этой точке равно 3,879: |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
∑j=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка не является наихудшей. Эта точка становится точкой . |
|||||||||||||||||||||||||||||||||||||||||
Условие останова не выполняется: |
)2 + ( |
|
|
|
|
|
|
− )2 = |
|||||||||||||||||||||||||||||||||
f ( |
|
|
|
|
|
|
|
|
|
|
|
|
) |
= |
( |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
(x0 )− f (x1 ) |
|
= |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
(x1 )− f (x2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
(x2 )− f (x0 ) |
|
|
= |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
