
Исследование операций и методы оптимизации
..pdf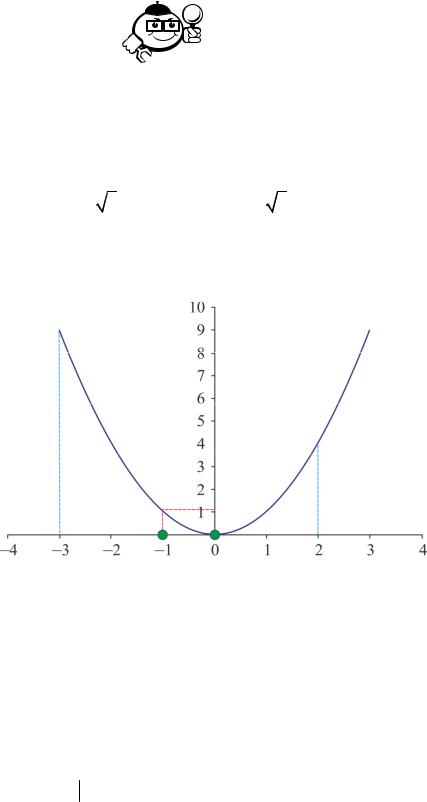
|
б) если L |
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
> l , положить k = k +1 и перейти к шагу 4. |
|
|||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
Пример 1.4 ······················· |
|||
······················· |
|
|
|
|
|||||||||||
|
Выполним поиск минимума рассмотренной на рисунке 1. функции ме- |
||||||||||||||
тодом золотого сечения. Пусть начальный интервал равен |
[−3;2]. Точность |
||||||||||||||
l = 2. |
Вычислим величины |
y0 , z0 (рис. 1.8): |
|
5 (2 − (−3))= −1,09; |
|||||||||||
|
y = a |
+ |
3 |
− |
|
5 (b |
− a |
) = −3 + 3− |
|||||||
|
0 |
0 |
z |
|
|
2 |
|
+ b |
0 |
− y |
0 |
= −3 + 2 |
2 |
|
|
|
|
|
0 |
= a |
|
0 |
− (−1,09) = 0,09. |
|
|||||||
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|||
|
Рис |
|
|
|
|
|
|
|
|
|
ция 1) |
|
||
|
Значения функции в точках: |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
f (y |
) = (−1,09)2 =1,19; |
|
|
|
|
||||
|
Выполняется условие: |
|
f (z0 |
= (0,09)2 |
= 0,01. |
|
|
|
y = 0,09, |
|||||
z |
|
f (y0 |
> f (z |
0 |
). Значит, a = −1,09, b = 2 , |
|||||||||
= −1,09 + 2 − 0,09 = 0,82 (рис. 1.09). |
|
|
1 |
1 |
|
1 |
||||||||
1 |
Вычисляем L |
= |
b |
− a |
|
= 2 − (−1,09) |
= |
3,09 . Эта величина |
|
больше задан- |
||||
|
|
|
||||||||||||
ной точности (l = 2), |
поэтому |
|
переходим |
|
следующей итерации. |
|
|
|||||||
|
k |
|
1 |
1 |
|
функции в точках y , z : |
|
|
|
|
||||
|
Рассчитаем значения |
|
|
|
|
|
||||||||
|
|
|
|
|
|
f (y |
) = (0,09)2 |
= 0,01; |
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (z |
22 |
= 0,67. |
|
|
|
||
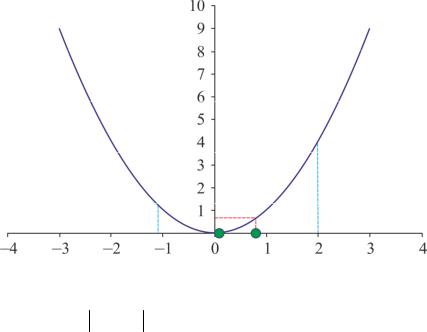
Так как f (y |
) |
≤ f (z |
) |
) = (0,82)2 |
|
и |
y = −1,09 + |
||||||
то1 |
полагаем |
a |
|
= −1,09, b = 0,82 |
|||||||||
+ 0,82 − 0,09 |
= −0,36, |
z2 |
= 0,09. |
|
|
2 |
|
2 |
|
2 |
|||
|
1 |
|
|
1 |
|
|
|
|
|
|
|||
Рис |
|
|
|
|
|
|
|
|
|
|
|
|
ция 2) |
Вычисляем L = |
b |
|
− a |
= 0,82 − (−1,09) =1,91. Полученное знач |
|||||||||
еньше точности, поэтому поиск минимума завершается и в качестве решения |
|||||||||||||
можно взять точку: |
1 |
|
2 |
|
2 |
|
|
|
|
|
|
||
|
x* = |
a |
+ b |
= |
−1,09 + |
0,82 |
= −0,135. |
||||||
|
|
|
2 |
2 |
2 |
|
2 |
|
|||||
································ ·········· ····························· |
|||||||||||||
Таким образом, алго итм схож с методом дихотомии, отличие заключает- |
|||||||||||||
ся в выборе точек для определения поведения функции: в методе дихотомии |
|||||||||||||
малое число откладывалось по обе стороны от средней точки, в методе золото- |
|||||||||||||
го сечения берутся точки золотого сечения. |
|
|
|||||||||||
1.4.4 Метод Пауэлла |
|
|
|
|
|
|
|
|
|
|
|
||
Этот метод основан на последов тельном применении процедуры оцени- |
|||||||||||||
вания с использованием квадратичной |
аппроксимации [2]. |
||||||||||||
Алгоритм |
– начальная точка; ∆x |
– выбранная величина шага по оси x , |
|||||||||||
Пусть x |
|||||||||||||
ε > 0 и δ > 0 –1 |
заданные точности. |
|
|
|
|
||||||||
Шаг 1. Вычислить |
x |
2 |
= x |
+ ∆x . |
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Шаг |
2. Вычислить |
|
( |
|
) и |
|
|
( |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, если |
|
( ), |
|||||||||||||||||||||
то |
|
3. Если |
|
|
|
( |
|
|
) > |
|
( |
|
|
) , положить |
|
|
= |
|
|
|
+ |
|
∆ |
( ) ≤ |
|||||||||||||||||||||||||
|
= |
|
|
− ∆ |
|
. Если x |
|
< x |
, то перенумеровать точки в естественном порядке: |
||||||||||||||||||||||||||||||||||||||||
x = x , |
x = x , x = x . |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
( |
|
), |
|
|
( |
) |
и |
|
( |
|
), найти |
|
|
|
|
|
|
|||||||||||||
1 |
|
Шаг 4. Определить |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
3 |
|
2 |
|
|
1 |
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
равно точке |
x |
|
, которая соответствует |
|
|
|
|
, используя квадратичную |
|||||||||||||||||||||||||||||||||||
|
|
Шаг 5. По трем точкам |
|
|
= |
|
вычислить |
|
|
|
|||||||||||||||||||||||||||||||||||||||
аппроксимацию: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
|
|
|
|
|
|
} |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
− |
|
f (x |
)− f (x ) |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x ) |
− f |
(x |
) |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a2 = x − x |
|
a |
|
|
x3 |
− x |
2 |
1 |
1 |
|
|
|
|
x2 |
|
|
− x 1 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
( |
) |
− |
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
x |
|
3 |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Шаг 6. Проверка на окончание поиска: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
а) |
|
|
F |
|
|
− f |
(x ) |
|
|
≤ ε; |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
б) |
|
|
Xmin |
|
− x |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
≤ δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Если |
условия а) и б) выполняются одновременно, то закончить поиск |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(в качестве |
результата взять точку |
|
|
). Иначе переход на шаг 7. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
Шаг 7. Выбрать «наилучшую» точку ( X |
|
|
|
или |
) и две точки по обе |
||||||||||||||||||||||||||||||||||||||||||
стороны от нее. Обозначить эти точки в естественном порядке и перейти на |
|||||||||||||||||||||||||||||||||||||||||||||||||
шаг 4.Замечание: после пятого шага необходимо провести дополнительную |
|||||||||||||||||||||||||||||||||||||||||||||||||
проверку, |
|
. к. точка |
|
|
|
может находиться за интервалом |
( |
|
) |
. В этом случае |
|||||||||||||||||||||||||||||||||||||||
точка |
|
заменяется |
|
|
|
|
|
и осуществляется переход к шагу 1. |
|
|
|
||||||||||||||||||||||||||||||||||||||
·················· · ···· |
|
|
|
|
|
|
|
|
|
Пример 1.5 |
······················· |
||||||||||||||||||||||||||||||||||||||
|
|
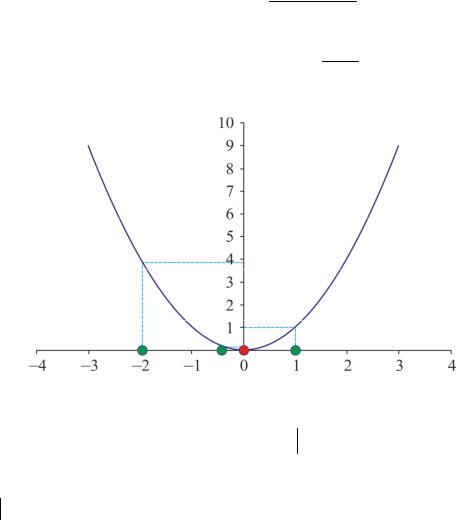
Рассмотрим применение |
|
|
|
|
|
|
|
|
для функции (рис. 1.3). Пусть началь- |
||||||||||||||||||||||||||||||||||||||
ная точка равна x |
= − |
|
|
|
∆ |
= |
|
алгоритмаε = δ = . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Вычислим x |
|
= x |
|
+ ∆x = − |
+ |
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
(x |
|
|
|
|
24 |
|
|
|
|
|
= 4; |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) = (−2)2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x |
|
) |
|
= (−0,5)2 |
|
= 0,25. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Так как |
f (x > f (x |
|
) |
|
|
то x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x ) =1 = |
||||||||||||||
|
|
|
|
= x + 2∆x = −2 + 2 1,5 =1, |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
F = min{f , f , f |
|
} |
= |
|
|
|
|
|
, |
3 |
X |
|
|
1 |
= −0,5. |
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||||||||
|
1 |
|
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
По трем точкам |
|
, x |
0,25x вычислим |
, используя квадратичную |
||||||||||||||||||||||||||||||||||||||||||||
min |
|
2 |
|
|
3 |
|
|
f (x )− f |
|
|
min |
|
|
|
|
|
0,25 − 4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
симацию (рис. 1.10): |
|
|
|
|
1 |
|
(x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
a |
= |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= −2,5; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
x |
− x |
|
|
|
|
|
|
|
−0,5 − |
(−2) |
|
|
|
|||||||||||||||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
) |
|
|
|||||||||||||||||||||||
|
a2 = |
x |
|
|
x |
|
|
|
|
|
|
|
x3 |
|
|
x |
|
|
1 |
|
|
|
− |
|
|
x2 |
x |
|
1 |
|
|
= |
|
|||||||||||||||
|
|
|
− |
|
|
|
|
|
|
1 |
− |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
− |
4 |
|
|
|
|
|
|
0,25 |
− 4 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
0,5 |
2 |
|
1 |
|
|
|
|
|||||||||||||||
|
|
= 1− |
(−0,5) 1 |
|
|
(−2) − |
(− |
) |
=1; |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
− |
|
− − |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
+ x |
|
|
|
|
a |
|
|
|
|
|
−0,5 |
− 2 |
|
|
−2,5 |
|
|
|
|
|
|||||||||||||||||
|
|
|
x |
= |
|
|
|
2 |
2 |
1 |
− |
|
2a1 |
|
= |
|
|
2 |
|
|
− |
|
2 |
|
1 |
= 0. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. аппрок-
Проверим окончание поиска |
|
F |
− f (x ) |
≤ ε : |
|||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
• |
условие не выполняется |
|
|
|
0,25 − 0 |
|
≤ 0,1; |
||||||
|
|
|
|||||||||||
|
|
−0,5 − 0 |
|
≤ 0,5 выполняется. |
|
|
|
|
|
|
|||
• |
|
x является x , т. . значение функции |
|||||||||||
|
|
|
|
|
или |
||||||||
Наилучшей |
|
точкой |
X |
|
|||||||||
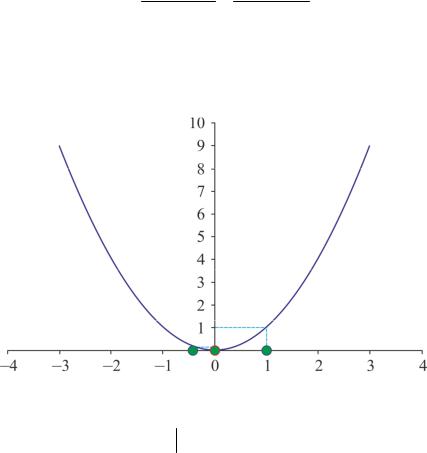
в этой точке минимально изравноmin0. Нужно выбрать две точки по обе стороны
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
от неё. Это будут точки −0,5 и 1. Обозначим эти точки в естественном поряд- |
|||||||||||||||||||||||||||||||||||||||||||||||||
ке: |
x |
= −0,5, x |
f |
= 0, |
x =1. |
|
|
|
|
= 0,25; f (x |
) = 0 |
|
|
|
|
f (x |
) =1 =1. |
||||||||||||||||||||||||||||||||
|
|
|
(x ) = (−0,5) |
|
|
|
|
= |
|
||||||||||||||||||||||||||||||||||||||||
|
1 |
|
2 |
1 |
3 |
|
|
|
|
|
|
|
|
F |
|
|
|
|
= min{f |
2, f |
|
|
, f |
|
}=0;. |
|
3 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
min |
|
|
|
|
|
Xmin |
1 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Вычислим |
(рис. 1.11): |
|
|
|
|
|
|
|
= |
0. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
)− f |
|
(x |
) |
|
|
|
|
0 − 0,25 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
f |
(x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
− x |
|
|
|
1 |
|
|
|
|
0 |
− (−0,5) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
a = |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= −0,5; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
(x |
|
)− f |
|
) |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
(x |
|
|
|
|
f (x )− f (x |
) |
|||||||||||||||||||||||||
|
|
|
|
|
a2 |
|
x |
|
|
|
|
x |
|
|
|
|
2 |
1 |
|
x 1 |
|
|
|
|
|
|
|
|
|
x2 |
x 1 |
|
|||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
− |
|
|
|
|
= |
|||||||||||||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
− |
|
|
|
|
0,25 |
− |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
1 |
1 |
0 |
1− |
0,25 |
|
|
− |
|
0 |
− |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
− |
1 |
|
− ( |
−0,5) |
0 |
− (−0,5) |
=1; |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
+ x |
|
|
|
a |
|
|
|
|
0 |
− |
0,5 |
|
−0,5 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
x |
= |
|
|
|
|
2 |
2 |
|
1 − 2a1 |
= |
|
|
|
2 |
|
|
|
|
− |
2 1 = 0. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверим окончание поиска |
F |
− f ( |
x |
) |
|
≤ ε : |
|
|||||||
|
|
|||||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
• |
|
|
− 0 |
|
|
|
≤ 0,1 выполняется; |
|
|
|
||||
|
|
|
|
|
|
|
||||||||
• |
е |
|
0 − 0 |
|
|
|
≤ 0,5 также выполняется; |
|
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
• |
условия |
|
окон |
|
чания поиска |
|
|
|
|
|
в качестве решения прини- |
|||
|
|
|
|
|
|
|
||||||||
|
мается точка |
|
|
x = 0, значениевыполняются,функции этой точке равно f (x ) = 0. |
||||||||||
·······································································

1.5 Методы, основанные на использовании производных |
|
|
|
|||||||||||||||||||||||||||
Данные методы предполагают вычисление производной, ледовательно, |
||||||||||||||||||||||||||||||
к функции предъявляют требование |
|
|
|
|
|
|
|
|
|
|
|
. Вычисление произ |
||||||||||||||||||
водной может быть выполнено аналитическидифференцируемостил бо помощью формул числен |
||||||||||||||||||||||||||||||
ного дифференцирования. Приведем |
простейшие |
формулы численного диффе- |
||||||||||||||||||||||||||||
ренцирования. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вычисление первой пр изв дной. В качестве приближенных формул пер- |
||||||||||||||||||||||||||||||
вой производной можно использовать: |
|
|
|
) |
|
( |
|
) |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
f |
′(x)≈ |
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
f |
′(x)≈ |
|
|
|
+ |
|
|
− |
|
|
|
|
|
|
|
|
|
||||||||
Здесь |
|
– шаг. |
|
|
|
( |
) |
|
|
|
( |
|
|
) |
|
|
|
|
|
|
||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Формула с большей точностью: |
|
|
− |
|
|
− |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вычисление второй производной. В качестве приближенных формул вто- |
||||||||||||||||||||||||||||||
|
|
|
|
f ′ |
|
x |
|
≈ |
|
|
|
( |
|
|
|
) |
|
|
( |
|
) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
рой производной можно использовать: |
|
|
− |
|
− |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|||
1.5.1 Метод Ньютона |
|
|
|
|
( − )− 2 (2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
)+ ( + ) |
|
|
|
|
||||||||||||||||||||
|
|
|
f ′′(x) |
≈ |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пусть |
|
– унимодальная, дважды дифференцируемая на |
= |
[ |
] |
|||||||||||||||||||||||||
функция [2]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 , построим последовательность |
||||||||||||||
Выбрав начальное приближение |
|
|
||||||||||||||||||||||||||||
Считая неравенство |
|
|
|
|
|
xn+1 |
= xn − |
|
|
′′ |
( |
n ) |
|
|
|
|
|
|
|
|
||||||||||
f ′(xn+1 ) ≤ ε |
(ε |
– малое число) условием достижения |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′( |
) |
|
|
|
|
|
|
|
|
|
требуемой точности вычислений, |
|
положим x* ≈ xn+1. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
······················· |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.6 ······················· |
||||||||||||||||
Рассмотрим применение данного метода для поиска минимума функции |
||||||||||||||||||||||||||||||
( ) = |
(рис. 1.3). Пусть начальная точка |
x |
= |
, точность ε = . |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|

Первая производная равна: |
0 |
|
|
|
|
2 )′ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Вторая производная: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
′( |
|
) = ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Новое значение |
|
f ′(x |
|
) = |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
равно: x |
= |
|
− |
|
2 2 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
f ′′(x) = |
( |
x)′ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ′(x ) |
|
|
|
|
|
|
f ′(x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Выполним проверку условия: |
|
|
|
≤ ε, |
|
|
) |
|
= |
|
= . Данное значе- |
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
меньше точности |
ε , следовательно, |
выполнение |
|
алгоритма завершается |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ниев качестве решения принимается точка x* |
|
= x |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
······································································· |
||||||||||||||||||||||||||||||||||||
1.5.2 Метод средней точки |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функция. |
||||||||||
Пусть |
|
– унимодальная, дифференцируемая на |
|
= |
|
|
|
|||||||||||||||||||||||||||||
Рассмотрим алгоритм метода средней точки [2]. |
|
|
|
|
|
|
|
|
|
|
[ |
|
] |
|
, ε > |
– |
||||||||||||||||||||
Шаг 1. Задать начальный интервал неопределенности |
|
= |
|
|
|
|||||||||||||||||||||||||||||||
точность. |
|
|
|
|
|
= . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
|
] |
|
|
|
Шаг 2. Положить |
|
|
|
|
|
|
|
zk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Шаг 3. Вычислить среднюю точку |
= |
|
|
|
|
|
|
|
|
|
′( |
). |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Шаг 4. Сравнить |
′( ) |
с нулем: |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
а) |
если |
|
′( k )< |
, положить |
|
+1 |
|
= |
|
|
, |
|
+1 |
= |
|
|
и перейти к шагу 5; |
|
||||||||||||||||||
б) |
f ′(zk ) > |
|
+1 |
|
= |
|
|
, |
|
+1 |
= . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Шаг 5. Проверить условие окончания: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
а) |
если |
|
f ′(zk ) |
≤ ε , процесс поиска завершается и в качестве прибли- |
||||||||||||||||||||||||||||||||
|
женного решения можно взять точку |
x* = z |
k |
|
; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
б) |
если |
|
f ′(zk ) |
|
> ε , положить |
= |
+ |
|
|
и перейти к шагу 3. |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
······················· |
28 |
Пример 1.7 ······················· |
|
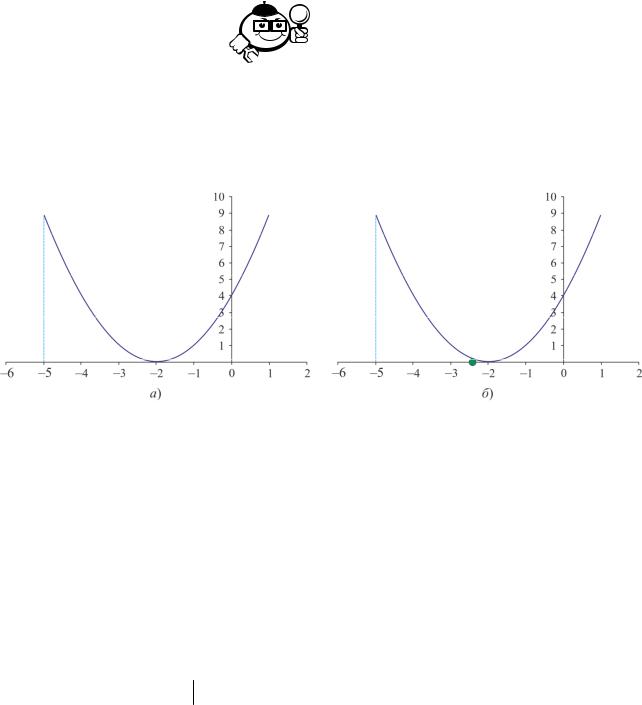
Рассмотрим поиск минимума функции f (x) = (x + 2)2 методом средней |
|
точки интервале [−5;0], ε = 0,5 |
(рис. 1.12). Как видно из рисунка, минималь- |
ное значение функции, равное нулю, наблюдается в точке −2.
|
|
|
|
|
|
Рис. 1.12 – График функции |
|
f (x) = (x + 2) |
|||||||||||||||||
Вычислим |
z0 |
a |
+ b |
−5 + 0 |
= −2,5 |
(рис. 1.12, б). |
|||||||||||||||||||
= 0 |
2 |
0 = |
2 |
||||||||||||||||||||||
Производная функции равна: |
|
= 2(x + |
2). |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f ′(x) |
|
|
|
|
|
||||||||
Значение производной в средней точке |
z0 |
: |
= −1. |
|
|||||||||||||||||||||
Так как |
f ′(z |
|
|
|
|
f ′( |
−2,5) = 2 |
(−2,5 |
+ 2) |
|
|||||||||||||||
|
)< 0 , то положим |
a = z |
|
= −2,5, b |
= b = 0. |
||||||||||||||||||||
Поскольку |
|
|
f |
′(z0 ) > ε, то переходим к расчету новой средней точки. |
|||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
1 |
|
0 |
z = |
a + b |
|
|
|
5 0 |
|
= −1,25 (рис. 1.13, а). |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= |
|
− + |
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
2 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
: |
|
|
|
|
|
|||
Значение производной в средней точке |
|
|
1,5. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
f ′(−1,25) = 2 |
(−1,25 |
+ 2) = |
|
|
||||||||||
Так как |
f ′(z |
) > 0, установим |
a |
|
= a |
|
|
|
1 |
|
|
|
= z = −1,25. |
||||||||||||
|
= −2,5, b |
||||||||||||||||||||||||
Критерий останова снова не выполняется. |
|
2 |
|
1 |
|||||||||||||||||||||
z2 = |
a |
+ b |
|
|
1 |
−2,5 |
−1,25 |
|
|
2 |
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
= −1,875 (рис. 1.13, б). |
|
|
|||||||||||||||||||
2 |
2 |
2 |
= |
|
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
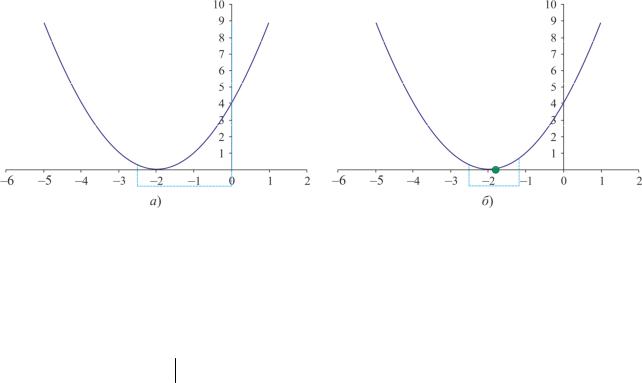
29
Рис. 1.13 – Вторая и третья итерации метода средней точки |
|
|||||||||||||
Значение производной |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
f ′(−1,875) = 2(−1,875 + 2) = 0,25. |
= −1,875. |
|
|||||||
f ′(z ) > 0, поэтому установим a = a |
= −2,5, b = z |
|
||||||||||||
Условие2 |
|
f ′(z |
|
) |
< 0,5 выполняется,3 |
поэтому2 |
работа3 2 |
алгоритма завершает- |
||||||
|
|
|||||||||||||
ся и в качестве |
|
решения |
принимается точка |
z |
|
= −1,875. |
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
······································································· |
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1.6 Решение задачи определения цены на товар |
|
спроса |
||||||||||||
Предприятие, изменяя цену на товар |
price, фи сировало |
|||||||||||||
demand . В итоге |
помощью метода наименьших квадратов значениебыл построена |
|||||||||||||
функция зависимости спроса от цены: |
|
|
|
|
|
|
|
|
||||||
Тогда |
|
|
|
|
demand |
= 90 −17,92 price. |
|
|
|
|||||
|
|
|
|
выручки |
income |
предприятия от цены может быть |
||||||||
представленазависимостьпомощью уравнения: |
|
17,92 price). |
|
|
||||||||||
|
|
|
|
|
income = price (90 − |
|
|
|||||||
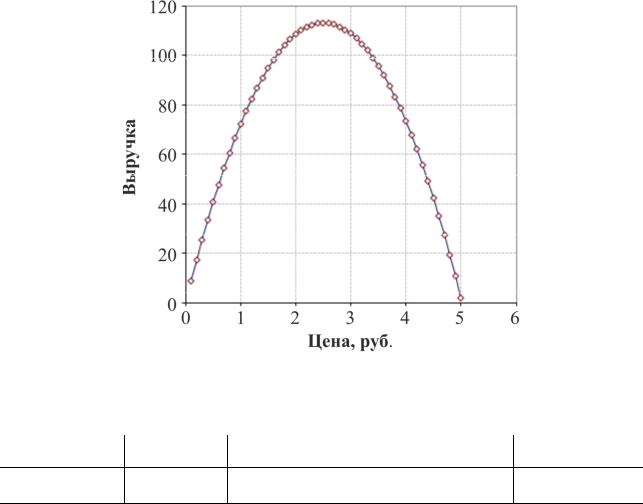
График этой функции представлен на рисунке 1.14. |
|
|
||||||||||||
Задача заключается в определении цены, при котор й выручка будет мак- |
||||||||||||||
симальной. Задачу определения максимума функции |
можно свести к |
адаче |
||||||||||||
определения минимума путем умножения функции на |
−1. Тогда минимизируе- |
|||||||||||||
мая функция имеет вид: |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
f ( price) = − price (90 −17,92 price). |
с ша- |
||||||||
Воспользуемся методом |
|
|
|
|
поиска на интервале [0;5] |
|||||||||
гом 0,1. Результаты представленыравномерноготаблице 1.1. |
|
|
|
|
||||||||||
Минимальное значение функции достигается в точке price = 2,5. |
|
|||||||||||||
30
|
|
|
|
Таблица 1.1 – Результаты равномерного поиска |
4,9 |
|
|
|
5 |
|
|
||||||||||||||
|
|
|
|
0,1 |
|
|
… |
2,4 |
2,5 |
|
|
|
2,6 |
|
… |
|
|
|
|
|
|||||
( |
) |
|
0 |
–8,821 |
|
|
|
–112,781 |
|
|
–113 |
|
|
–112,861 |
|
|
–10,741 |
|
|
|
–2 |
|
|||
|
Решим |
|
задачу с |
|
использованием |
|
метода |
|
Ньютона |
|
(начальная точка |
x |
|
0 |
= |
5, |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
ε = 0,1). Для этого будем использовать итерационную формулу: |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
xn+1 = xn |
− f |
′(xn ). |
|
|
|
|
|
|
|
|
|
|
|||||
|
Производная функции имеет вид: |
|
|
f |
′′(xn ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
f ′(x ) = 35,84x − 90. |
|
|
|
|
|
|
|
|
|
||||||||
|
В начальной точке значение производной функции равно 89,2: |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
n |
89,2. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
f ′(5) = 35,84 |
5 − 90 = |
|
|
|
|
|
|
|
|
|
||||||||
|
Значение второй произ |
дной равно |
f ′′(x |
|
) = 35,84. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
Вычислим значение новой точки: |
|
|
|
|
|
n |
= 2,511. |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
= x |
− f ′(x0 ) = 5 − |
89,2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
0 |
f ′′(x ) |
|
|
|
35,84 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
