
Исследование операций и методы оптимизации
..pdf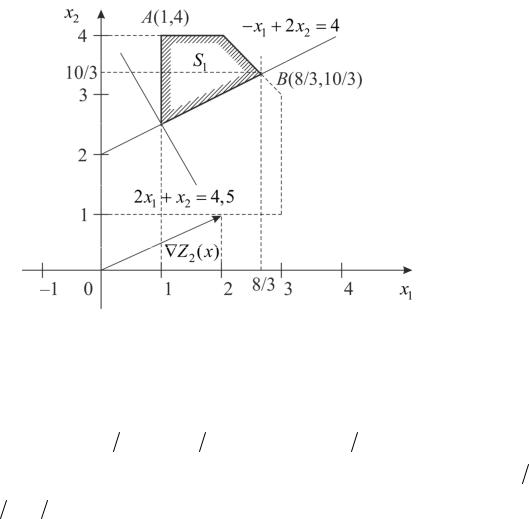
пать более чем на ∆ |
|
|
|
121 |
|
Z* − ∆ = 4 |
, то дополнительное |
|||
|
. Так как в нашем примере |
|||||||||
ограничение будет иметь вид: |
−x |
+ 2x |
|
≥ 4. |
1 |
1 |
|
(3.26) |
||
|
1 |
|
|
|
|
|
|
|
||
Задачу (3.23), (3.25), (3.26) также решаем графически (рис. 3.14). |
|
|||||||||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
Рис |
|
|
|
|
|
|
|
Z |
|
при условиях (3.25), (3.26) достига- |
||||||
|
|
Получаем, что максимум функции |
|
||||||||||||||||||
ется в точке B |
части S |
|
области S , так что2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
x** = 8 3; x** = |
10 3; Z |
* = Z (B) = 26 3. |
|
|
||||||||||||
|
|
Теперь |
|
1 |
|
по |
критерию |
|
Z |
|
|
на величину уступки |
|
= 5 3 |
|||||||
|
|
уступаем |
|
|
|
∆ |
|||||||||||||||
|
Z* − ∆ |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
( |
2 |
= 26 3− 5 3 = 7 |
) |
и получаем второе2дополнительное ограничение:2 |
(3.27) |
||||||||||||||||
2 |
|
|
|
|
|
|
2x |
+ x |
|
≥ |
7. |
|
|
||||||||
|
|
Максимизируем функцию Z |
(3.24) при условиях (3.25), (3.26) и (3.27). |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
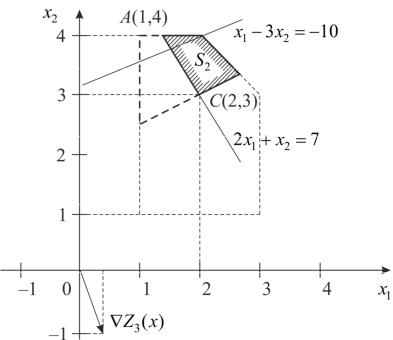
Решение этой задачи графическим 3методом представлено на рисунке 3.15. |
|
||||||||||||||||||||
|
|
Таким образом, получаем оптимальное решение рассматриваемой трех- |
|||||||||||||||||||
критериальной задачи (точка |
C на рис. 3.15): |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
x*** = |
2; |
x*** |
= 3. |
|
|
|||||||
|
|
Соответствующие значения1частных2 |
критериев при этом составляют: |
||||||||||||||||||
|
|
|
|
|
|
|
|
Z = 4; |
Z |
2 |
= |
7; |
Z |
3 |
= −7. |
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
122
Рассмотрим задачу об оптимальном ассортименте (табл. 3.6). Пусть в |
о |
|||||||||||||||||||
дели используются два критерия оптимальности: максимизация прибыли и |
ми- |
|||||||||||||||||||
нимизация трудозатрат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ограничение на объем сырья имеет вид: |
|
|||||||||||||||||||
Кроме того, переменные |
x |
|
4x |
+ 2x |
|
≤ 50. |
|
|||||||||||||
|
≥ 0, x |
|
|
|
≥ 0 (количество товара не может быть |
|||||||||||||||
отрицательным). |
|
|
|
|
|
1 |
|
1 |
|
2 |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Целевые функции: |
|
+ x |
|
|
8 − 3 → max (максимизация маржинальной |
|||||||||||||||
• |
f |
|
x |
,x |
= x |
10 − 4 |
|
|
|
|||||||||||
|
прибыли); |
1 |
( |
) |
|
2 |
( |
|
) |
|
|
|
|
|
|
|||||
|
f |
( |
1 |
2 |
|
|
|
|
|
|
|
|
|
|||||||
• |
|
x |
,x |
= 5x +10x |
|
→ min (минимизация трудоемкости). |
|
|||||||||||||
Пусть |
∆ = 20. |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
( |
1 |
2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Н йдем решение первой задачи (максимизация маржинальной прибыли) |
||||||||||||||||||||
при ограничении на объем ресурсов (рис. 3.16). |
|
|||||||||||||||||||
Для решения задачи минимизации трудоемкости добавим условие: |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6x |
+ 5x |
|
|
|
≥105. |
|
|||
По ученное решение представлено на рисунке 3.17 (заданные ограниче- |
||||||||||||||||||||
ния целевая |
функция п едставлены на рисунке 3.18). Таким образом, нужно |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
произвести 5 единиц товара 1 и 15 единиц товара 2. |
|
|||||||||||||||||||
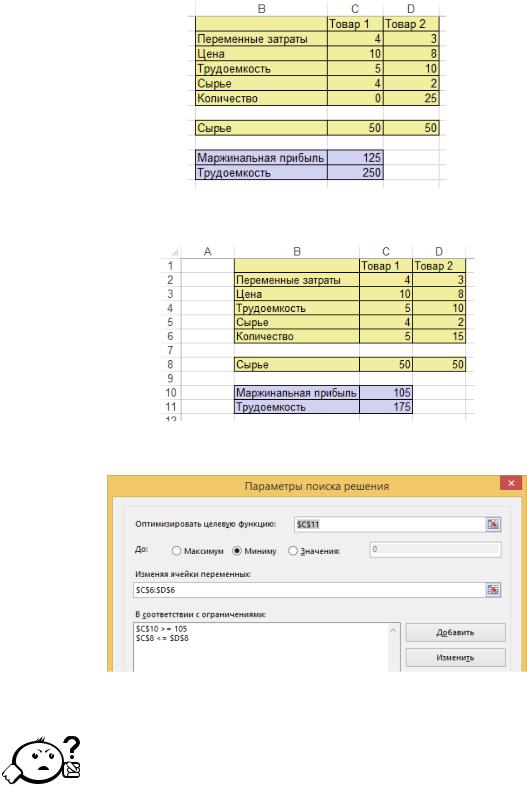
Рис. 3.16 – Решение |
маржинальной прибыли |
Рис. 3.17 |
трудоемкости |
|
····························································· |
|
Контрольные вопросы по главе 3 |
1 |
····························································· |
задачи линейного программирования? |
|
2. |
В чем суть графического метода решения задачи линейного програм- |
3 |
мирования? |
В чем состоит основная идея симплекс-метода? |
|
4 |
Опишите алгоритм симплекс-метода. |
5. |
Как происходит поиск разрешающей строки в симплекс-таблице? |
6 |
происходит поиск разрешающего элемента в симплекс-методе? |
|
7 |
Какие существуют методы поиска начального базиса? |
|
8 |
|
преобразования? |
9. |
симплексногокусственного базиса? |
|
10. |
В чем суть метода уступок? |
|
|
|
125 |
|
|
|
|
|
|
|
|
|
4 Транспортная задача |
|
|
|
||||||||
Важным част ым случаем задачи линейного программирования является |
|||||||||||
так называемая транспортная задача, которую можно сформулировать следую- |
|||||||||||
щим образом. |
|
|
|
|
|
|
|
|
|
|
|
4.1 Экономико-математическая модель транспортной задачи |
|||||||||||
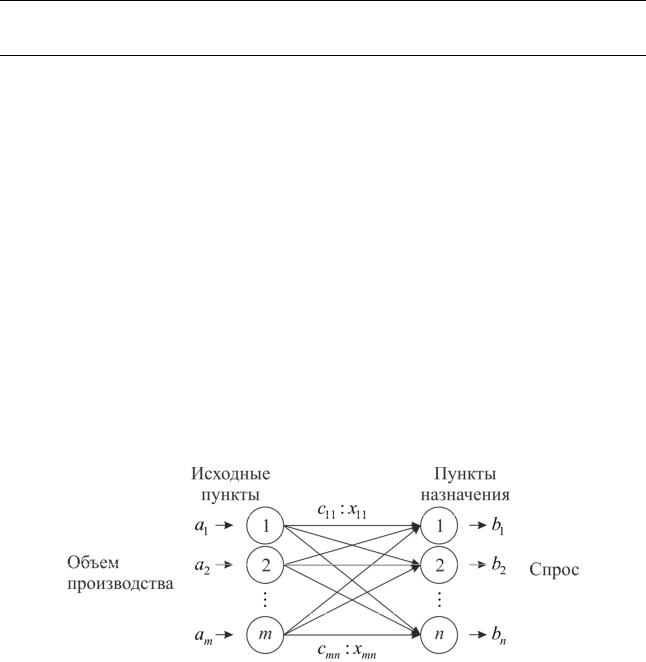
В m пунктах отправления |
A , |
A |
,…, |
A |
|
, кот рые |
|
дальнейшем будем |
|||
называть поставщиками, сосредоточено |
пределенное количество единиц неко |
||||||||||
торого однородного продукта, которое |
обозначим a (i =1,...,m). Данный про |
||||||||||
|
1 |
2 |
|
|
|
m |
|
|
|
|
|
дукт потребляется в n пунктах B |
,B |
,…,B |
, |
|
которыеi будем называть потреби- |
||||||
телями; объем потребления обозначим |
n |
b |
|
|
( j =1,...,n) |
(рис. 4.1). Известны |
|||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
расходы на перевозку единицы продукта из пункта A в пункт B , которые рав- |
|||||||||||
|
|
|
|
|
|
j |
|
|
c |
|
[1]. |
ны c и приведены в матрице транспортных расходов C = |
|
||||||||||
ij |
|
|
|
|
|
|
|
i |
( ij ) |
j |
|
|
|
|
|
|
|
|
|
|
|||
Рис. 4.1 – Геометрическая интерпретация транспортной задачи Требуется составить такой план прикрепления потребивывозитсяелей к поставщи-
кам,пункты. . план перевозок, при котором весь продукт из пунктов A в B в соответствии с потребностью и общая величина транспортныхi издержек будетj минимальной.
Обозначим количество продукта, перевозимого из пункта A в пункт B , через x . Совокупность всех переменных x для краткости обозначимi x , тогдаj целеваяijфункция задачи будет иметь вид: ij

|
|
|
|
|
|
|
f |
|
x |
|
= m |
|
|
n |
c |
x → |
|
(4.1) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
∑ ∑ ij |
ij |
|
|
|
|
|||||||
а ограничения будут выглядетьnследующим образом: |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
=1 j |
=1 |
|
|
|
|
|
(4.2) |
||||
|
|
|
|
|
|
|
|
∑ |
|
ij |
≤ |
|
|
i |
|
|
= |
|
||||||
|
|
|
|
|
|
|
|
j |
=1 |
|
≥ |
|
|
j |
|
|
= |
|
(4.3) |
|||||
|
|
|
|
|
|
|
|
∑ ij |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
x |
|
|
|
|
|
|
(4.4) |
||||
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
> |
|
|
|
|||||||
|
Первая группа ограничений (4.2) указывает, что суммарный объем пере |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
озок продукции из некоторого исходного пункта не может превышать п оиз |
||||||||||||||||||||||||
веденного количества этой продукции, вторая группа ограничений (4.3) требу- |
||||||||||||||||||||||||
ет, чтобы суммарные перевозки продукции в некоторый пункт потребления |
||||||||||||||||||||||||
полностью удовлетворяли спрос на эту продукцию. |
|
|
|
|
||||||||||||||||||||
|
Рассмотрим задачу, исходные данные которой представлены в табли- |
|||||||||||||||||||||||
це 4.1. |
|
|
|
Таблица 4.1 – Транспортная таблица. |
|
|
|
|||||||||||||||||
|
|
|
|
|
Стоимость доставки 1 кг конфет, д. е. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Город (спрос, кг) |
|
|
|
||
|
(производство, кг) |
|
|
Москва (2 000) |
|
|
|
(1 500) |
|
Новгород (800) |
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
Г род |
500) |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
Санкт-Петербург |
|
Нижний |
|
|||||
|
Подольск |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
7 |
|
||||
|
Балашиха |
(2 |
000) |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
15 |
|
|
16 |
|
||
|
Целевая функция |
|
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
f x |
= |
x |
|
|
+ x |
x |
+ x + x + x + x → |
||||||||||||||||
|
Ограничения: |
11 |
|
|
|
|
+ x |
|
|
+ x |
|
≤ |
22 |
23 |
|
|||||||||
|
|
|
|
12 |
|
|
|
|
|
13 |
|
|
|
21 |
|
|||||||||
|
|
|
|
|
|
|
|
x11 |
|
+ x12 |
|
+ x13 |
≤ |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x |
+ x |
|
|
≥ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
21 |
|
|
22 |
|
|
|
|
23 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
x11 |
+ x21 |
|
≥ |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
x21 |
|
+ x22 |
|
≥ |
|
|
|
|
|
||||
|
Полученное в Excel решение представлено на рисунке 4.2. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
32 |
|
|
|
|
|
|
|||

|
Из модели (4.1)–(4.4) видно, что суммарный объем производства в исход- |
||||||||||||||||
ных пунктах |
m |
не должен быть меньше суммарного спроса в пунктах назна- |
|||||||||||||||
чения |
|
n |
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
m |
|
= n |
|
|
|
|
(4.5) |
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то мод ль называют сбалансированной (закрытой) транспортной моделью. Она |
|||||||||||||||||
отличается |
от модели (4.2), (4.n3) тем, что |
j=1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
∑ |
|
|
|
|
(4.6) |
|
|
|
|
|
|
|
|
∑ ij |
= |
i |
|
= |
… |
|
|
|
||
|
|
|
|
|
|
|
|
j |
= |
j |
|
= |
… |
|
|
|
(4.7) |
|
|
|
|
|
|
|
∑ ij |
|
|
|
|
||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
······················· |
|
i |
|
|
Пример 4.1 |
······················· |
|||||||||||
|
|
|
|
||||||||||||||
|
Заводы автомобиль ой фирмы |
|
|
|
в п. |
. Центры распре- |
|||||||||||
деления (пункты |
назначения) |
расположенырасположены. |
|
. Объемы |
в |
||||||||||||
спроса |
в п. |
|
|
равна 2 300 и 1 400 автомобилей ежеквартальнпроизводства, . . суммар |
|||||||||||||
. |
|
|
равны 1 000, 1 500, 1 200 |
автомобилей |
ежеквартальн . Величина |
||||||||||||
ный объем произ одства равен суммарному спросу (3 700 |
автомобилей |
еже |
|||||||||||||||
биля из п. |
|
(условиеп. |
|
указана |
в таблице 4.2. |
|
|
|
|
||||||||
квартально) |
|
|
(4.5) выпол |
яется). Стоимость перевозки одного автомо- |
|||||||||||||
|
|
|
|
|
|
|
|
Таблица 4.2 – Стоимость перевозки |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пункты |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
назначения |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
215 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Исходнпунктые |
|
|
|
|
100 |
|
|
108 |
|
|
|
|
|
|
|
||
Модель |
|
|
|
|
|
|
С |
|
102 |
|
|
68 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x + x + x + |
x + x + x → |
||||||||||||||||||||||
f (x) = |
|
|
||||||||||||||||||||||||
|
21 |
+ x |
|
=1000; |
12 |
|
21 |
|
|
22 |
|
|
31 |
|
|
32 |
|
|
||||||||
|
+ |
|
22 =1500; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
11 |
|
12 |
=1200; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
31 |
+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ x |
|
+ x |
|
=1400; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
11 + x21 + x31 = 2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
xij |
≥ 0. |
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
12 |
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Занесем модель в таблицу 4.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Таблица 4.3 – Транспортная таблица |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
Спрос |
|
E |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 000 |
|
|
2 300 |
80 |
x |
1 |
|
400 215 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Объем производства |
|
|
|
|
1 500 |
|
|
|
|
|
|
100 |
12 |
|
|
|
|
108 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 200 |
|
x31 |
|
|
|
|
102 |
x32 |
|
|
|
68 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
······································································· |
|
|
|||||||||||||||||||||
······················· |
|
|
|
|
|
|
|
Пример 4.2 |
······················· |
|||||||||||||||||
|
Несбалансированная модель |
|
|
|
|
|
производит |
|||||||||||||||||||
|
Изменим условия |
|
|
примере 4.1. Предположим, что завод |
||||||||||||||||||||||
е 1 500, а 1 300 автомобилей. Это приведет к дисбалансу, поскольку суммар- |
||||||||||||||||||||||||||
ный объем производства (3 500) не равен суммарному |
осу (3 700). Другими |
|||||||||||||||||||||||||
слов ми, дисба анс означает, что спрос в цен рах распределения |
(в пунктах |
|||||||||||||||||||||||||
назначения) полностью |
удовлетворить не |
|
удается. В этом случае не бходимо |
|||||||||||||||||||||||
изменить транспортную модель таким образом, чтобы недостаток автомобилей |
||||||||||||||||||||||||||
( |
− |
= |
) оптимально распределился между |
|
. |
- |
||||||||||||||||||||
|
Введем фиктивный исходный пункт (фиктивный завод) с |
|||||||||||||||||||||||||
ностью 200 автомобилей. Стоимость |
|
|
|
|
|
|
|
с фиктивного заводапроизводитель. |
||||||||||||||||||
естественно положить равной нулю (тперевозок. . никакие перевозки не осуществляют- |
||||||||||||||||||||||||||
ся). Таким образом, сбалансированная модель имеет |
ледующий вид (табл. 4.4). |
|||||||||||||||||||||||||
Здесь |
|
– фиктивный завод. Если объем производства превышает спрос, мож- |
||||||||||||||||||||||||
но ввести дополнительные |
фиктивные пункты назначения. Пусть, например, |
|||||||||||||||||||||||||
в п. |
спрос упал |
2 300 до 1 900 автомобилей. В таблице 4.5 представлена |
||||||||||||||||||||||||
измененная модель (здесь |
– фиктивный пункт назначения). |
|
|
|||||||||||||||||||||||
|
|
Таблица 4.4 – Добавление фиктивного пункта-производителя |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 300 |
1 400 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
215 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 200 |
|
|
102 |
|
|
68 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
108 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
Таблица 4.5 – |
|
Добавление |
|
фиктивного пункта-потребителя |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 900 |
|
|
1 400 |
|
|
400 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
215 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 200 |
|
|
102 |
|
|
|
68 |
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
108 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
130 |
|
|
Автомобили, поступающие с некоторого завода в фиктивный пункт наз |
|||
начения, представляют собой избыток производства на этом заводе. Соответ- |
||||
ствующая стоимость перевозки равна нулю. Однако можно назначить штраф за |
||||
хранение автомобилей на складе завода, тогда стоимость перевозки одного ав |
||||
томобиля (п репроизведенного) будет равна штрафу за его хранение. Анало |
||||
гично |
модели |
с недопроизве енным |
автомобилей. Каждую не- |
|
допоставленную |
еди ицу |
продукции количествомпункт назнач ния можно обложить |
||
штра-фом. Тогда транспортные расходы на единицу недопроизведенной про- |
||||
дукции равны штрафу за недополученную продукцию. |
||||
······································································· |
||||
······················· |
Пример 4.3 ······················· |
|||
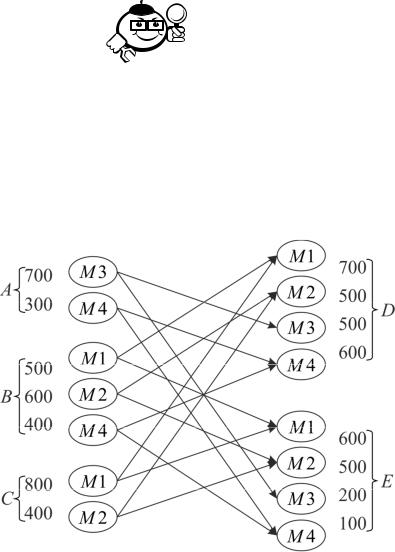
|
Многопродуктовая транспортная модель |
|||
|
Пусть автомобильная компания (заводы |
A, B, C ) производят автомоби |
||
четырех различных марок M1, M 2, M3, M 4, причем завод A выпускает модели |
||||
M 3, M 4 ; завод |
B – M1, M 2, M 4 ; завод C – |
M1, M 2 (рис. 4.3). В таблице 4.6 |
||
приведены объемы выпуска и спроса автомобилей всех марок.
Предположим, что стоимость перевозок автомобилей любой марки одинакова (стоимость перевозки на одну милю).
