Исследование операций и методы оптимизации

Если найден столбец, содержащий хотя бы один положительный элемент

(если таких столбцов несколько взять любой из них), отметить его вертикаль-

ной стрелкой (см. табл. 3.7) и перейти к шагу 3.

Шаг 3. Разделить свободные члены

соответствующие полож тельные

числа из выделенного столбца

выбрать

наименьшее

частное. Отметить стро

ку, соответствующую наименьшему частному горизонтальной стрелкой. Выде-

разрешающий элемент

, стоящий на пересечении отмеченных строки

литьстолбца. Перейти к шагу 4.

Шаг 4.

и

, остальные переменные оста-

1.

Поменять местами переменные

2.

вить на прежних местах.

.

На место опорного элемента поставить число

3.

На остальных местах разрешающей (опорной) строки записать соот

ветствующие элементы исходной таблицы, делённые на опорный эле-

4.

мент.

На свободные места разрешающего столбца поставить со знаком «ми-

нус» соотв тствующие элементы исходной таблицы, делённые на

опорный элемент.

Шаг 5. Оставшиеся свободные места в новой СТ заполнить построчно

следующим образом: из строки элементов исходной таблицы вычесть произве

дение ее элемента из разрешающего столбца на уже заполненную разрешаю-

щую строку новой таблицы.

-й базисной переменной имеем:

Например, для строки

Знак «←» сто

т на месте элемента разрешающего столбца, заполненного

согласно определению операции 4.

,

,

, +1

,

(

, +1

¬

,

)=

(

,

+1

¬

)−

(

¬

)

·······················

Пример 3.6

·······················

Решить ЗЛП симплекс-методом:

x

x

− x

4

+ x

=

1

5

2

+ x

+

x

=

+ x

4

x

5

f

x

−

=

=

3+ x

4−

x

5→

являются базис-

4

5

Из системы ограничений видно, что переменные

ными. Эти переменные используем в качестве начального опорного плана

(начального базиса). Поэтому 1-й, 2-й

3-й столбцы

из таблицы. Ре-

зультаты расчета

в

таблице

3.8. Привед

решение.

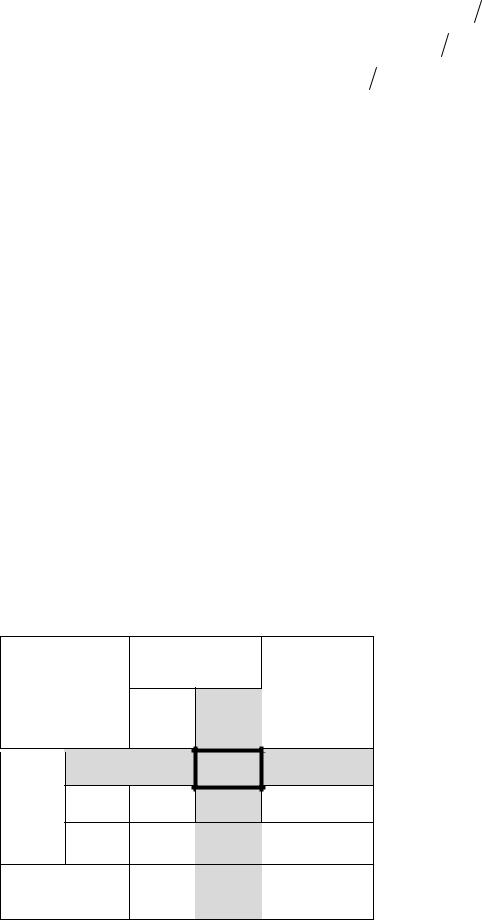
Шаг 1. В таблицепредставленыпоследней строке два элемента:исключаем1 –2. Один из них

является отрицательным, поэтому переходим к шагу .

Шаг 2. В столбце, соответствующем числу «–2», есть два положительных

элемента: 1 и 3. Выделяем столбец стрелкой.

Шаг 3. Разделим свободные члены на соответствующие положительные

числа из выделенного столбца:

1)

1

;

2)

7/3=2,33

) = .

и выберем наименьшее частное:

(

Отметим строку, соответствующую наименьшему частному горизонталь-

ной стрелкой (это первая строка). Выделим квадратом разрешающий элемент,

строкиоящий

на пере ечении отмеченных строки и столбца (пересечение первой

второго столбца – элемент «1»).

и

, остальные переменные

Шаг 4.

Поменять местами переменные

оставить на прежних местах.

= .

На место опорного элемента поставить число

На остальных местах разрешающей (опорной) строки запишем соответ

твующие элементы исходной

аблицы, делённые на опорный элемент. По-

скольку элемент равен единице,

то все значения останутся прежними.

Следовательно, элементы «3», «–2» и «–2» второго столбца будут изменены на

«–3», «2», «2».

Шаг 5. Оставшиеся свободные места в новой СТ заполнить построчно

следующим образом: из строки элементов исходной таблицы вычесть произве

дение ее элемента из разрешающего

лбца на уже заполненную разрешаю-

щую строку новой таблицы (

,

-я строка,

-й столбец).

Элемент первого столбца второй строки

(

)

будет преобразован: − ×

×(− ) = +

=

. Преобразование последующих элементов:

a

a

2,3

=

−

=

= − (− ) (−

) = − = −

3,1

a

=

− (−

)

=

+

=

3,3

Элементы последней строки:

p

= − (− ) (− ) = − = −

p1

= − − (− )

= − + =

3

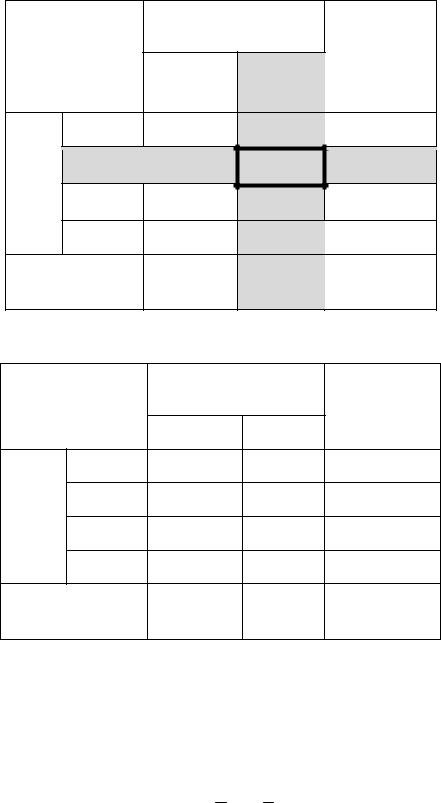
Заполнение новой таблицы 3.8, б закончено и происходит переход к ша-

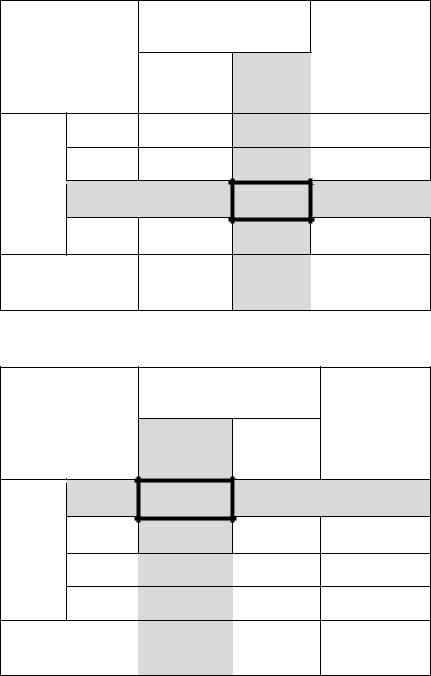
гу 1. Шаг 1. В таблице в последней строке два элемента: –1 и 2. Один из них

является отрицательным, поэтому переходим к шагу 2.

сть один положитель-

Шаг 2. В столбце, соответствующему числу «–1»

ный элемент: 5. Следовательно, вторая строка будет

разрешающей.

квадратом разрешающий элемент, стоящий на пересечении вто-

рой строкиВыделимпервого столбца – элемент «5».

и

, остальные переменные

Шаг 3. Поменяем местами переменные

оставить на прежних местах.

.

На место опорного элемента поставить число 1 =

На остальных местах разрешающей (опорной) строки запишем соответ

ствующие элементы исходной таблицы, делённые на опорный элемент. Полу

ч

м элем нт второй строки второго столбца: −

= −

. Элемент второй стро-

ки

третьего

столбца:

=

. Элемент

второй

строки третьего столбца:

Следовательно, элемент первой строки первого столбца будет равен: −(− )

=

=

. Элемент третьей строки первого столбца будет равен:

−

−

.)

=

.

Элемент четвертой строки первого столбца будет равен: −

(

−

)

= (

Шаг 4. Оставшиеся свободные места в новой СТ заполнить построчно

следующим образом: из строки элементов исходной таблицы вычесть произве

дение ее элемента из разрешающего столбца на уже заполненную разрешаю-

щую строку новой таблицы:

a

= − (− ) (− ) = −

=

a1,2

=

− (−

) (− ) =

+

=

a1,3

=

− (−

) (− ) =

−

=

3,2

a

=

−

(− ) =

+

=

3,3

Элементы последней строки:

p

=

−

(

−

)

(

−

)

=

−

=

За

2

p

=

−

−

)

=

+

=

3

лнение новой таблицы (табл. 3.8, в) завершено, переходим к шагу 1.

В посл дней строке все элементы положительны, следовательно, решение

задачи

найдено. Полученное

решение:

x

=

x

2

=

x =

x

4

=

x

= .

1

3

5

Подставляя решение в исходную функцию, получим её значение:

= 3

+

−

− x

=

+

−

= −

5

Таблица 3.8а – Решение задачи симплекс-методом (первая итерация)

Небазис

переменные

Свободные

члены

–1

↓

2

→

1

2

3

7

переменныеБазис

1

–2

1

1

–2

–3

Целевая

функция

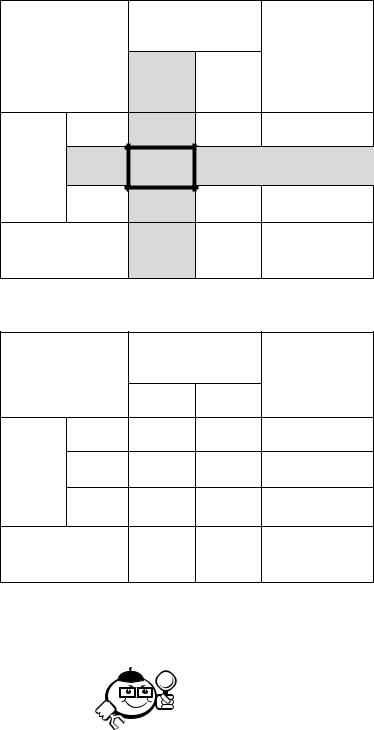
Таблица 3.8б – Решение задачи симплекс-методом (вторая итерация)

Небазис

переменные

Свободные

члены

↓

1

2

–1

→

5

–3

1

переменныеБазис

–1

2

5

1

Целевая

функция

Таблица 3.8в – Решение задачи симплекс-методом (решение)

Небазис

Свободные

переменные

члены

0,2

0,4

2,2

0,2

–0,6

0.2

переменныеБазис

0,2

1,4

5.2

0,2

1,40

1.2

Целевая

функция

f

= − .

Ответ: x* =

*

·······································································

·······················

·······················

Решить ЗЛП симплекс-методом: Пример 3.7

при ограничениях

f (x) =

x

+

x

→

x

1

2

+

x

2

≤

1

x + x

2

≤

1

x2 ≤

x

≤

1

Приведем задачу к стандартному виду с помощью дополнительных пере-

менных:

x +

x

2

+ x

=

1

3

x + x

+ x

=

1

2

4

x2 + x5 =

x

+ x

=

1

6

Дальше решаем симплексным методом (табл. 3.9, а–г).

Таблица 3.9а – Симплекс-таблица (первая итерация)

Небазис

переменные

Свободные

члены

1

↓

8

3

2

1

16

переменныеБазис

→

0

1

5

3

0

21

Целевая

–2

–3

0

функция

Таблица 3.9б – Симплекс-таблица (вторая итерация)

Небазис

переменные

Свободные

члены

↓

–3

3

→

1

2

–1

11

переменныеБазис

0

1

5

3

0

21

Целевая

–2

3

15

функция

Таблица 3.9в – Симплекс-таблица (третья итерация)

Небазис

переменные

Свободные

члены

1

↓

3

–3

→

–2

5

5

переменныеБазис

0

1

5

–3

9

12

Целевая

2

–3

21

функция

Таблица 3.9г – Симплекс-таблица (результат)

Небазис

Свободные

переменные

члены

1

3

6

–2/5

1/5

1

переменныеБазис

2

4

3

–9/5

3

Целевая

4/5

3/5

24

Ответ:

функция

f * = .

x* = (

)

Таким образом, мы можем записать

3

1

=

+ 5

−

5

2

1

=

−

+

=

+ 5

−

5

3

9

=

−

+

5

5

Коэффициенты целевой функции, полученные в последней строке, мы

взяли со

ком «минус», так как мы умножали целевую функцию на –1. Опти

мальное

значение

целевой функции берем со знаком «плюс» (потому что в ис-

=

−

−

ходной задаче мы ищем максимум

).

·······································································

·······················

Пример 3.8

·······················

Решить ЗЛП симплекс-методом:

при ограничениях

Z =

y

+

y

2

+

y

+

y

4

→

1

y

3

y

y

y

+

+

≥

+ y

2

+ y

≥

1

i

4

y

≥

=

3

1

2

со знаком «минус» [1]. По-

Вводим дополнительные переменные

лучим стандартную ЗЛП

y

i

y

y

− y

+

+

=

y

+ y

2

+ y

− y

=

1

i

4

5

y

≥

=

3

6

1

2

. Для этого первое урав-

В качестве базисных переменных возьмем

i

нение разделим на 3. Выразим базисные переменные через свободные

y

=

−

y

− y

2

+ y

3

1

6

и подставим в целевую функцию, получим

=

−

−

+

Дальше решаем симплексным методом (табл. 3.10, а–в).

=

−

−

+

+

Таблица 3.10а – Симплекс-таблица (первая итерация)

Небазисные переменные

Свободные

члены

↓

1

0

–1

3

→

3

переменныеБазис

1/3

2/3

–1/3

0

2/3

–4

–3

7

5

–29

Целевая

функция

Таблица 3.10б – Симплекс-таблица (вторая итерация)

Небазисные переменные

Свободные

члены

1/3

↓

0

–1/3

1

1/3

→

–1/9

5/9

–1/3

1/9

1/3

переменныеБазис

4/3

–5/3

7

11/3

–25

Целевая

функция

Таблица 3.10в – Симплекс-таблица (решение)

Небазисные переменные

Свободные

2/5

–3/5

1/5

–2/5

члены

4/5

переменныеБазис

–1/5

9/5

–3/5

1/5

3/5

1

3

6

4

–24

Целевая

функция

) Z* = .

Ответ: y* = (

=

−

+

−

+

·······································································

=

+

−

+

−

=

+

+

+

+

3.3.4 Поиск начального базиса

Для решения задачи ЛП симплексным методом необходимо получить

начальный опорный план (начальный базис).

Рассмотрим спос б получения начального базиса (начальной угловой

точки многогранника допустимой

области). Если в исходной задаче ЛП огра-

ничения заданы в виде неравенств, например,

(3.19)

n

≤

=

∑ ij

j

i

,

,..., =

приве-

j=1

то введение дополнительных переменных

1

=

+1

2

=

+2

дет (3.19) к виду:

i =

n

j

+

Вектор

X = y y

i − ∑ ij

=

являться

начальным

опорным

2

y

m

j=1

будет

1

планом (начальным базисным решением).

Метод имплексного преобразования

де равенств (то есть

Е ли ограничения исходной задачи ЛП заданы в в

имеем сразу

стандартную фор

у ЗЛП), то для получени

начального базиса

можно воспользоваться

методом симплексного преобразования, который явля-

ется одной из модификаций метода Гаусса – Жордана [1].

Запишем систему

n

j

=

i

=

в виде таблицы 3.11.

∑ ij

. Алгоритм симплексного

j=1

При этом предполагается, что все

≥

=