
Исследование операций и методы оптимизации
..pdf
при ограничениях: x + x |
2 |
≥ |
≤ x ≤ |
|
|
|
|
|
≤ x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
≤ |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.2.6 Задача об оптимальном ассортименте |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Имеются два вида товара, характеризующиеся цен й, переменными за- |
|||||||||||||||||||||||||||||
тратами, трудозатратами (время на изготовление одного |
|
товара), необходимым |
||||||||||||||||||||||||||||
количеством сырья (табл. 3.6). На предприятии существует ограничения трудо- |
||||||||||||||||||||||||||||||
затрат (80 часов) и сырья (50 кг). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Таблица 3.6 – Исходные данные |
Товар 2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Товар 1 |
|
|
|
|
|
||||||||||||||
|
|
|
Ц Характеристикана, д. . |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
8 |
|
|
|
|
||||||
|
|
|
Переменные. . |
затраты, |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||
|
|
|
Трудозатраты, час |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|||||
|
|
|
Сырье, кг |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
Необходимо определить |
|
|
|
|
|
|
|
|
|
|
товара |
|
каждого вида, имеющее мак |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
симальную маржинальную прибыль,количествопри этом трудозатраты и сырье не долж- |
||||||||||||||||||||||||||||||
ны превышать ограничений. |
|
|
|
|
|
|
|
|
|
|
|
модель задачи. Обозн чим |
, |
– |
||||||||||||||||
|
Составим экономико- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
равны |
+ |
(см. рис. 3.7),математическуюобъем необходимого сырьятрудозатратысостави |
+ |
. |
||||||||||||||||||||||||||
количество товаров первого |
второго вида. Тогда |
бщие |
|
|
будут |
|||||||||||||||||||||||||
Получим систему неравенств: |
|
|
x + |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
(3.15) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x + |
|
|
x |
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
|||||
|
Кроме того, переменные |
|
1 |
x |
|
|
|
|
2 |
|
|
(количество товара не может быть |
||||||||||||||||||
|
x |
≥ |
|
|
|
≥ |
|
|
|
|||||||||||||||||||||
отрицательным). |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Маржинальная прибыль составит: |
|
|
|
|
|
|
+ x ( − |
|
|
|
|
|
(3.16) |
||||||||||||||||
|
|
|
|
|
f (x x ) = x ( |
|
|
|
− |
|
) |
) |
|
|
|
|
||||||||||||||
|
Итак, экономико-математическая модель задачи: определить |
|
|
|||||||||||||||||||||||||||
товаров каждого вида |
= ( |
1 |
) |
, удовлетворяющего системе (3.15)количествоусловию |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
(x ≥ |
|
x ≥ |
), при котором функция (3.16) принимает максимальное значение. |
|||||||||||||||||||||||||||
1 |
Решением задачи являются значения: |
x |
= |
|
|
x |
|
= |
кг. |
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Трудоемкость составит: |
x + |
|
x |
|
= |
|
|
|
+ |
|
|
|
= часов. |
|
|||||||
Расход сырья: |
x |
+ |
x |
|
= |
|
|
|
|
2 |
+ |
|
|
|
= |
кг. |
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, ограничения задачи выполняются. |
|
|
|
|
|||||||||||||||||
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Маржинальная прибыль составит: |
|
|
|
|
|
|
|
д. е. |
|
|
|||||||||||
f |
(x x |
) = x |
( − |
) |
+ x |
2 |
( − |
) = |
|
|
|
||||||||||
|
1 |
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.3 Решение задач линейного программирования |
|
|
|||||||||||||||||||
3.3.1 Графический метод решения задач |
|
|
|
|
|
|
|||||||||||||||
линейного программирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Графический метод применяют, когда число переменных не превосхо |
|
||||||||||||||||||||
дит 2. На практике задачи такой размерности встречаются редко, однако графи |
- |
||||||||||||||||||||
ческий метод хорошо иллюстрирует основные понятия, используемые |
|||||||||||||||||||||
шении ЗЛП большой размерн сти. Графический метод рассмотрим на примере |
|||||||||||||||||||||
задачи (задача технического |
контроля) |
[1]. |
|
|
······················· |
||||||||||||||||
······················· |
|
|
|
|
|
|
|
Пример 3.4 |
|||||||||||||
|
|
|
|
|
|
x |
x +=x |
|
≥ + |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
≤ |
|
|
x |
|
|
≤ |
|
|
|
|
|
|
||
|
|
|
|
|
|
x1 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≥ |
|
|
x2 |
|
|
≥ |
|
|
|
|
|
|
|||
В качестве первого шага решения |
2 |
следует определить допустимую об- |
|||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
ласть, или область допустимых решений (ОДР). |
|
|
всех огран чений. Все |
||||||||||||||||||
Для изображения ОДР следует наче ти ь |
|
|
|||||||||||||||||||
допустимые решения лежат в первом |
квадранте,графикит. . x x |
2 |
≥ |
(см. рис. 3.7). |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
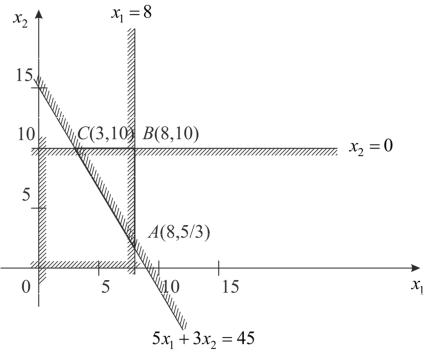
ОДР задачи является треугольник93ABC (рис. 3.8) (в общем случае много-
точек. Нужно найти точку, в которой f (x) = min .
гранник M при m > 2 ), кот рый содержит бесконечное число допустимых
Если зафиксировать значение ЦФ |
|
f = 40x |
+ 36x |
|
, то соответствующие |
|||||
ему точки будут лежать на некоторой прямой. При изменении величины f |
||||||||||
прямая |
|
|
|
|
|
|
1 |
|
2 |
|
параллельному переносу. При поиске максимума линия |
||||||||||
смещаетсяподвергаетсяаправлении |
д ента, при поиске минимума – антиградиента до |
|||||||||
точки последнего касания границы ОДР. |
|
|
|
|
|
|
||||
Рассмотрим прямые, соответствующие различным значениям f , имею |
||||||||||
ие с ОДР хотя бы одну общую точку. Построим линию уровня ЦФ, проходя- |
||||||||||
щую через ОДР, например, через точку |
|
B(8,10) |
. Значение ЦФ в этой точке |
|||||||
f (8,10) = 40 8 |
+ 36 10 = 680, построим прямую |
|
|
|
||||||
|
f (x) = 680 |
40x |
+ |
36x = 680 |
|
|||||
|
|
10x |
+ |
9x |
|
=170. |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
Также укажем на рисунке направление антиградиента ЦФ (рис. 3.9): |
||||||||||
|
|
1 |
|
2 |
−40 |
|
|
|
||
|
|
|
|
40 |
|
|
|
|
||
|
|
|
|
36 |
|
−36 |
|
|
|
|
|
|
−f (x) = − |
|
|
|
= |
. |
|
|
|
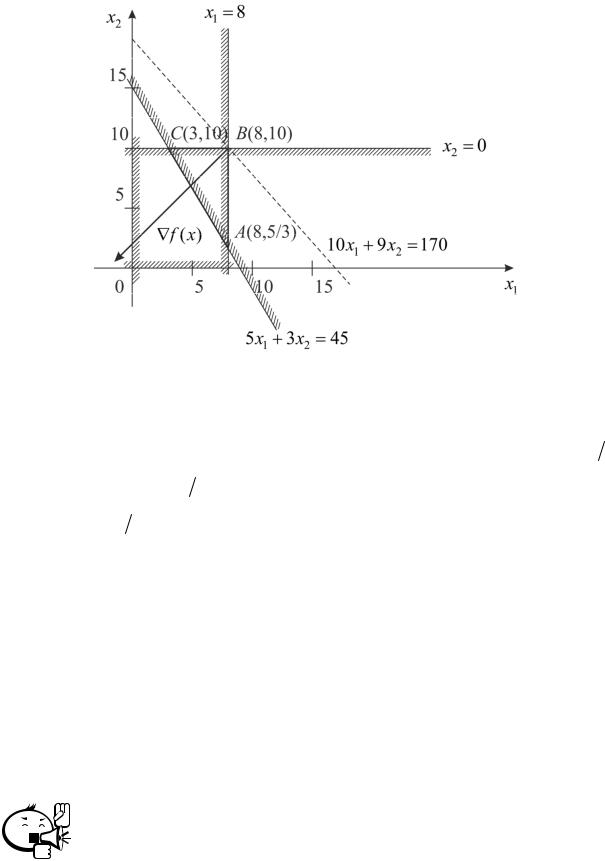
94
|
|
Рис |
|
|
|
нта |
f умень- |
|
|
При приближении прямой |
ЦФ |
к началу координат значение |
|||
шается. Минимальное значение |
достигается в узловой точке |
A(8, 5 3). |
|||||
Следовательно, x = (8, 5 3); f |
= 380 |
– оптимальное решение задачи. Таким |
|||||
образом x = (8, 5 3) – оптимальный план. |
|
||||||
|
|
Итак, для |
режима работы ОТК необходимо использовать |
||||
8 контролеров 1-оптимальногоразряда |
1,6 контролера 2-го разряда. Дробное зна |
||||||
x |
2 |
=1,6 соответствует ситуации, |
|
когда один из двух К2 используется в течение |
|||
неполного рабочего дня. При недопустимости неполной загрузки контро ер в |
|||||||
дробные знач ния обычно округляются, получая приближенное оптимальное |
|||||||
целочисленное решение x = 8, |
x |
2 |
= 2. |
|
|
||
|
|
1 |
|
|
|
|
|
·······································································
Из рассмотренногосоответствуетпримера р шения задачи ОТК мы видим, что оптимальное решение задачи одной из вершин многогранника.
·····························································
Отсюда можно сделать исключительнообластиважный вывод: оптимальное решение – координаты вершины допустимых решений.
·····························································
|
95 |
Из этого вывода следует метод решения задач линейного программирова- |
|
ния, который заключается в следующем: |
|
1. |
Найти в ршины области допустимых решений как точки пересечения |
2 |
ограничений. |
Определить последовательно значения целевой функции в вершинах. |
|
3. |
Вершина, в которой целевая функция приобретает оптимальное (max |
4. |
или min) значение, является опт мальной вершиной. |
Координаты оптимальной вершины есть оптимальные значения иско- |
|
|
мых переменных. |
·····························································
Возможны следующие частныепрямаяслуч и:
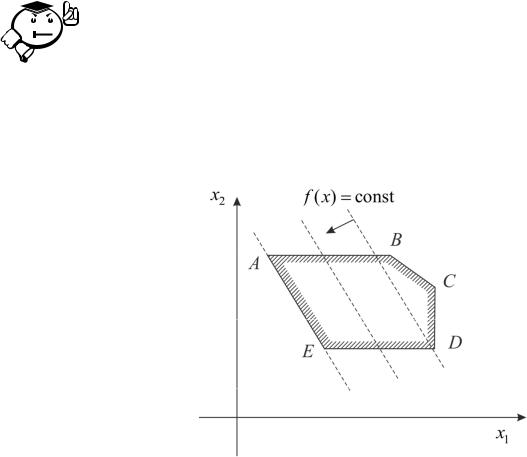
1. При параллельном переносе f x const совпадает множествоодной из сторон многогранника решений. Имеем бескточканечное AE решенийоптимальным(р с. 3.10). В данном примере( ) =каждая от-
резка является решением.
Рис. 3.10 |
решений |
2. ОДР не ограничена сверху (так |
называемый «стакан», |
рис. 3.11). |
|
Если антиградиент направлен ко «дну стакана» (вниз), то за- чаед ча будет иметь решение только на минимум, в противном слу
– только на максимум.
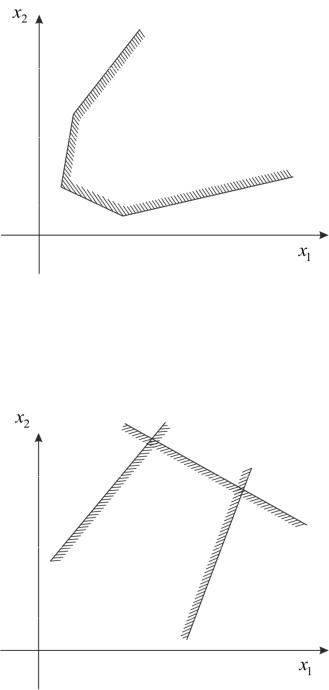
96
3. ОДР не ограничена снизу («перевернутый стакан», рис. 3.12).
Аналогично, если антиградиент направленнако «дну стакана» (вверх),случаето з дача будет иметь решение только минимум, в противном – только на максимум.
·····························································
3.3.2 Основы симплекс-метода
Рассмотрим общую(канонической)ЗЛП m ограничениями и n переменными, записанную в стандартной форме:
|
|
|
|
|
|
|
|
f (x) = ct x = |
n |
|
|
c |
j |
x |
j |
|
→ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
n |
n = |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
+ |
x |
|
|
+…+ |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
≥ 0; |
|
|
j |
=1,n. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|||
|
Как правило, число уравнений задачи меньше числа переменных (т. е. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
j |
|
+…+ |
|
|
|
|
|
= |
|
|
|
|
|
|||||||
< |
), поэтому множество |
|
допуст мых решений равно ∞ . Задача состоит |
|||||||||||||||||||||||||||||
в том, чтобы найти наилучшее решение |
|
в смысле принятого |
критерия (мини- |
|||||||||||||||||||||||||||||
мума целевой функции). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Выше было отмечено, что оптимальное решение представляет собой одну |
|||||||||||||||||||||||||||||||
из вершин многогранника допустимой области. Другими словами, оптимальное |
||||||||||||||||||||||||||||||||
решение – это одно из базисных решений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Получение одного из базисных решений основано на известном класси |
|||||||||||||||||||||||||||||||
ческом методе решения систем линейных уравнений – |
|
тоде Гаусса – Жорда- |
||||||||||||||||||||||||||||||
а. Основная идея этого метода состоит в сведении системы |
|
уравнений с |
||||||||||||||||||||||||||||||
неизвестными |
к каноническому или ступенчатому виду при помощи элемен- |
|||||||||||||||||||||||||||||||
тарных операций над строками: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1) |
|
умнож ние |
юбого уравнения системы на положительное или отрица- |
||||||||||||||||||||||||||||
|
2) |
|
тельное число; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
прибавление к любому уравнению другого уравнения системы, умно- |
||||||||||||||||||||||||||||||
|
|
|
женного на положительное или отрицательное ч |
ло. |
|
|
||||||||||||||||||||||||||
|
При использовании первых |
|
|
переменных такая система имеет следую- |
||||||||||||||||||||||||||||
щий вид: |
|
|
|
|
0 |
+1 |
|
+1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
, |
|
0 |
|
(3.17) |
|||
|
|
|
|
|
1 |
+ |
, |
|
+…+ |
|
, |
|
|
|
|
+…+ |
|
= |
1 |
|
||||||||||||
|
|
|
|
|
+ |
1,m+1 |
m+1 |
+ |
…+ |
1,s s |
+ |
… |
+ |
1,n n |
= |
|
|
|||||||||||||||
|
Подставляя эти переменные в целевую функцию, получим |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
+ |
, |
+1 |
|
+1 |
+ |
…+ |
|
, |
|
|
n |
+ |
…+ |
|
|
= |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
( |
) |
= |
0 |
+ |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
j |
∑ |
|
|
|
|
|
|
|
|
|
|
|
|||
где |
0 = |
|
m |
0 |
0 = − m |
0 |
|
|
j |
|
|
|
|
|
=m+1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
+ |
|
|
= |
|
+ |
|
|
… |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
∑ i |
i |
j |
∑ i |
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
i=1 |
|
|
i |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
Систему уравнений можно переписать следующим образом: |
(3.18) |
||||||||||||||||||
|
|
|
|
|
|
|
i |
= |
0 − |
|
n |
|
|
0 |
j |
= |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
i |
j |
∑ |
|
|
ij |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
=m+1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
····························································· |
|||||||||||||||||||
|
|
|
|
|
Переменные |
|
… |
|
, входящие с |
|
|
|
коэффициен- |
||||||||||
|
|
|
|
тами в одно уравнение1 |
системы (3.17),единичными(3.18) |
нулевыми – в |
|||||||||||||||||
|
|
|
|
остальные, называются базисными |
или |
зависимыми. В канониче- |
|||||||||||||||||
|
|
|
|
ской системе (3.17), (3.18) каждому уравнению соответствует |
|||||||||||||||||||
|
|
|
|
ровно одна базисная переменная. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
····························································· |
|||||||||||||||||||
или |
|
Остальные |
( − |
) переменные |
|
|
( |
+1 |
… |
) |
называются |
небазисными |
|||||||||||
|
|
переменными. |
|
|
|
|
|
|
|
|
|
|
|
можно полу- |
|||||||||
|
|
|
независимымиПри писи системы в каноническом виде все ее решен |
||||||||||||||||||||
чить, |
рисв ивая |
независи |
|
ым переменным про звольны |
значения и решая |
||||||||||||||||||
затем получающуюся систему относительно |
ависимых переменных. |
||||||||||||||||||||||
|
|
|
|
Базисным решением системы (3.17) |
называется решение, полученное при |
||||||||||||||||||
нулевых значениях небазисных переменных. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Например, в системе (3.17) одно из базисных решений задается как |
|||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
0 |
, |
2 |
= |
0 |
,…, |
m = |
0 |
|
|
|
|
|
||
|
|
|
|
|
|
= 1 |
2 |
m |
|
|
|
|
|||||||||||
|
|
|
|
|
|
x |
|
|
= |
0;…; x |
|
|
= |
0 |
|
|
|
|
|
|
если |
||
|
|
|
|
|
|
m+1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Базисное решение называется допустимым базисным |
|||||||||||||||||||
значения входящих в него базисных переменных |
|
j ≥ |
= |
|
решением,что эквива- |
||||||||||||||||||
|
|
||||||||||||||||||||||
лентно условию |
0 ≥ |
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как различные базисные реш ния системы (3.14) соответствуют раз- |
|||||||||||||||||||
личным вариантам выбора |
( ) |
из |
общего числа |
( |
) |
переменных , то число |
|||||||||||||||||
допустимых базисных решений (угловых точек) не превышает |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
cm |
= |
|
|
n! |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
n |
|
|
( |
|
− |
) |
|
|
|
|
|
|
|
|
|
|
|
Поэтому ЗЛП можно решать посредством перебора конечного числа уг- |
|||||||||||||||||||
ловых точек допустимого множества |
|
, сравнивая значения ЦФ в этих точках. |
|||||||||||||||||||||
Это наихудший вариант решения ЗЛП, |
т. к. требует огромного объема вычис- |
||||||||||||||||||||||
лений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

······················· |
|
|
|
|
|
Пример 3.5 ······················· |
|||||||||||||
|
Если |
= |
|
|
= |
|
(задача небольшой размерности), то количество пе- |
||||||||||||
реборов составит |
|
|
|
|
|
|
|
|
|
|
. Даже если ЭВМ будет вы- |
||||||||
полнять |
|
|
|
переборов вариантов(количество1 с,вариантов)ей потребуется 40 лет для поиска |
|||||||||||||||
решения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Обычно |
= |
|
|
|
|
|
= |
|
|
|
|
|
||||||
·········· ····························································· |
|||||||||||||||||||
|
|
|
|
|
|
|
Идея симплекс-метода (СМ) состоит в направленном перебо- |
||||||||||||
|
|
|
|
|
ре угловых точек допустимого множества |
с последовательным |
|||||||||||||
|
|
|
|
|
уменьшением ЦФ |
( |
) . |
|
|
|
|
||||||||
|
|
|
|
|
····························································· |
||||||||||||||
|
СМ разработал Дж. Данциг (американский ученый) в 1947 г. Этот метод |
||||||||||||||||||
также называют методом последовательного улучшения решения (плана). |
|||||||||||||||||||
|
Гарантии результативности СМ обеспечиваются следующей теоремой. |
||||||||||||||||||
|
|
|
|
|
····························································· |
||||||||||||||
|
|
|
|
|
|
|
Т орема |
|
конечности алгоритма симплекс-метода. Если су |
||||||||||
|
|
|
|
|
ществует оптимальное |
решение ЗЛП, то существует и базисное оп |
|||||||||||||
|
|
|
|
|
тимальное решение. Это решение может быть получено через ко |
||||||||||||||
|
|
|
|
|
нечное число шагов симплекс-методом, причем начать можно с лю- |
||||||||||||||
|
|
|
|
|
бого исходного |
базиса. |
|
|
|
|
|||||||||
|
|
|
|
|
····························································· |
||||||||||||||
3.3.3 Алгоритм симплекс-метода |
|
|
|
ть в виде так |
|||||||||||||||
|
Ручные вычисления по симплекс-ме оду удобно |
||||||||||||||||||
называемых |
симплекс- |
|
|
|
. Для |
удобства |
составл ниоформлясимплекс-таблицы |
||||||||||||
(СТ) будем считать, чтотаблицЦФ система ограничений переписаны в форме [1]: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
где |
|
0 = m |
|
0 |
0 = − m |
|
|
0 + |
= |
= |
j=m+1 |
|
|
||||||
|
|
|
|
+ … |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
0 + |
∑ |
0 |
|
||
|
0 |
|
|
∑ i |
i |
j |
|
∑ i |
ij |
j |
|
|
|
|
|||||
|
|
|
|
|
i=1 |
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
i |
+ |
n |
|
0 |
= |
0 |
= |
|
|
|
|
|
|
|
|
||
|
|
∑ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
ij j |
|
i |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
j=m+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По исходным данным заполняется исходная СТ (табл. 3.7). В первый |
|||||||||||||||||||||||||||||||
столбец выписывают базисные переменные, в последний столбец – свободные |
||||||||||||||||||||||||||||||||
члены. В первую строку выписывают |
ебазисные переме ные, в последнюю |
|||||||||||||||||||||||||||||||
строку – коэффициенты при переменных |
в целевой |
функции. В последней |
||||||||||||||||||||||||||||||
клетке последней строки заносим |
со знаком «минус». |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
В остальные клетки заносятся коэффициенты ограничений. |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Сформулируем алгоритм СМ применительно к данным, внесенным в таб- |
|||||||||||||||||||||||||||||||
лицу 3.7. |
|
|
|
|
Таблица 3.7 – Симплекс-таблица |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
Свободные |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
↓ |
|
|
|
|
|
|
|
члены |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
a0 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Целевая |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Шаг |
|
1. Выяснить, |
|
имеются |
|
ли |
|
|
последней |
|
строке таблицы |
|
отрицатель- |
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
ные числа ( |
|
не принимается во внимание). Если все числа неотрицательны, |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
то процесс закончен; базисное решение |
b0 |
… b0 |
… |
|
является оптималь- |
|||||||||||||||||||||||||||
ным: |
= . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1 |
|
|
m |
|
|
) |
|
|
|
|
|
|
, |
|||
|
Если в последней строке имеются отрицательные числа |
+1 |
|
|
+2 |
… |
||||||||||||||||||||||||||
перейти к шагу 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
трица- |
|||||||||
|
Шаг 2. Просмотреть |
|
|
|
|
|
|
соответствующий наименьшему |
|
|||||||||||||||||||||||
тельному числу |
|
0, |
+1 |
≤ |
|
столбец,≤ и выяснить, имеются ли в нем положительные |
||||||||||||||||||||||||||
числа |
|
|
|
= |
|
.kЕсли |
|
в одном из таких столбцов нет положительных чи- |
||||||||||||||||||||||||
сел, то оптимального |
решения не существует. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
ik |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
