Приборы и устройства оптического и СВЧ диапазонов

241

При m>0 лазер генерирует. Разность населенностей n в этом режиме не зависит от уровня накачки, тогда как выходная мощность лазера (пропорциональная m) линейно возрастает с ростом W

В 3-х уровневом лазере порог уровня накачки определяется двумя факторами: 1)временем жизни метастабильного уровня; 2)потерями резонатора.

Анализ выражений (9.3), (9.4) для четырехуровневой системы проводится аналогично. В 4-х уровневом лазере Wпор ограничена в основном потерями в резонаторе. При достижении Wпор, n прекращает расти. Оценим Pвых генератора непрерывного режима.

Полная мощность рассеивающаяся, в резонаторе, и излучаемая через зер-

рая теряется на излучение через зеркало. Если через τc обозначить часть времени жизни фотонов в резонаторе, обусловленную потерями излучения за счет прохождения его через зеркало, а τ0 – время жизни, обусловленное всеми прочими ви-

Оценки показывают, что для рубинового лазера длиной активного элемента ℓ =2÷ 5см и диаметром d=2÷ 3мм в генерации участвует только часть этого объема. Примем диаметр генерирующей области d=1мм, а l=4см. Тогда, используя полученное уравнение, получим Pвых≈10Вт [4,10,19].

9.4.2.Пички и режим свободной генерации

Первые же экспериментальные исследования работы твердотельных лазеров выявили существенную нестационарность их излучений. Даже при непрерывном питании лампы накачки излучение имеет вид импульсов, амплитуда которых и расстояние между которыми могут изменяться во времени. Эти импульсы называют пичками. Для рубиновых лазеров длительность пичков ~ 1 мкс, период ~ 10 мкс. Характер пичковой генерации зависит от свойств резонатора и уровня накачки. В резонаторах с плоскими зеркалами пички, как правило, носят нерегулярный характер. В резонаторах со сферическими зеркалами последовательность пичков может быть регулярной, незатухающей или затухающей к постоянному уровню.

Анализ пичкового режима является сложной математической задачей [4]. Это объясняется тем, что в генерации могут принимать участие много типов колебаний, сильно взаимодействующих друг с другом, однако, физические причины образования пичков просты и могут быть поняты на основе следующих соображений.

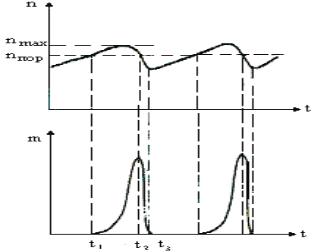
Пусть в начальный момент времени t = 0 в лазере включается сильное поле накачки, уровень которой будем предполагать постоянным. Под действием этого поля частицы перекачиваются на верхний метастабильный уровень. В некоторый момент времени t = t1 , разность населенностей n становится равной пороговой

242

nпор . При t> t1 , разность населенностей становится больше пороговой n > nпор , и

в результате возникает индуцированное поле, амплитуда которого быстро нарастает (рис 9.5.).

Рис. 9.5. Зависимость разности населенностей n и числа фотонов m в резонаторе лазера от времени

Возникновение поля и появление индуцированных переходов приводит к опустошению верхнего уровня. Рост n замедляется, затем прекращается и далее n начинает падать, достигая при t = t2 порогового значения. При t>t2, усиле-

ние в резонаторе меньше потерь и поле начинает падать. К моменту времени t = t3

поле исчезает, и n оказывается меньше порогового значения. Под действием накачки n снова начинает увеличиваться и процесс повторяется.

В тех случаях, когда пички не являются столь глубокими, как показано на рис.9.5, а представляют собой сравнительно небольшие колебания m относительно стационарного значения числа фотонов, их можно описать аналитически. Рассмотрим случай одномодовой генерации трехуровнего лазера. Примем, что

где mст и nст – стационарные значения m и n, а x и y малые отклонения m и

n относительно стационарных значений. Используя уравнения (9.2),(9.3) и (9.7) из предыдущего параграфа для х и у получим линейные дифференциальные уравнения

Уравнения (9.9) легко решаются. Исключим из (9.9) х. Тогда для у будет

Из (9.19) следует, что для рубинового лазера (при следующих параметрах: α = 2 , L=1м, l=10см, τ = 10−3 c , χ = 0.4см−1 ,ϑ = 3 ×1010 см. / c ) период следования пичков t0 = 10мкс , что по порядку величины соответствует экспериментальным данным.

Аналогичным образом можно оценить время затухания пичков. Оно имеет порядок 10−3 c и уменьшается с ростом накачки.

Пичковая генерация типична для подавляющего большинства лазеров, работающих в режиме свободной генерации. Этот режим реализуется при разряде батарей конденсаторов блока питания через лампу накачки. Время, в течение которого происходит разряд, составляет по порядку величину 10-3 с. Время затухания пичков в лазере имеет тот же порядок величины. Поэтому выход на стационарный режим в таких лазерах (т.е. регулярные пички), как правило, не происходит. Более того, в ряде случаев такой выход невозможен при любом увеличении длительности импульса накачки. Наличие пичков, а также хаотичность их во времени, является недостатком лазеров и препятствует ряду их применений.

Приведём некоторые цифры, характеризующие режим свободной генерации. Энергия излучения в импульсе колеблется от сотых долей джоуля до тысяч джоулей. Длительность импульса составляет 10-3с, и, соответственно импульсная мощность достигает десятков и сотен кВт, к.п.д. – может достигнуть нескольких процентов.

9.4.3.Лазер с модуляцией добротности

В режиме свободной генерации излучение твердотельных лазеров представляет собой импульс общей длительностью порядка 1 мс. Этот импульс состоит из множества пичков. Для ряда приложений лазеров таких как дальнометрия, оптическая локация, желательно иметь короткий и мощный моноимпульс. Получение моноимпульсов излучения длительностью 10 – 100 нс. и энергией в импульсе порядка 100 МВт возможно в лазере с модуляцией добротности. Принцип действия такого лазера состоит в следующем.

В режиме свободной генерации излучение света начинается в тот момент, когда разность населенностей рабочих уровней равна пороговому значению. Максимум излучения приходится на момент времени, когда эта разность вновь равна пороговой. В промежутке между этими моментами времени разность населенностей достигает максимального значения (см. рис. 9.7.) Очевидно, что энергия, излученная в «пичке», определяется тем, насколько разность населенностей «успела» превысить свое пороговое значение. Энергия, запасенная избыточным чис-

246

Для определения выходной энергии генератора и длительности импульса следует подставить (9.22) во второе уравнение (9.20) и провести его интегрирование. Ограничимся лишь оценками. Энергия(ϖ нач ), запасенная в образце на рабо-

чем переходе перед началом генерации, очевидно, равна

ϖ нач = N 2Hω ,

где N 2 – число атомов на уровне 2.

Энергия, излученная в импульсе, меньше ϖ нач , так как импульс заканчивается

в момент, когда часть частиц остается на втором уровне и полного высвечивания не происходит. При значительном превышении порога можно принять, что в кон-

Проведем численные оценки для рубинового лазера. Пусть кристалл имеет объем 5см3 и плотность активных частиц в нем составляет 1.6 ×1019 см−3 . Примем длину резонатора L=1м, коэффициент отражения зеркала R=0.5, N 2нач = 0.9N и

соответственно n2нач = 0.8N . Величина Hω на длине волны рубинового лазера равна 2.85 ×10−19 Дж . Подставляя эти значения в формулы (9.26), (9.27), (9.28), найдем:

R max = 0.7 ×109 Вт,

ϖ = 9.1Дж,

τ = 13нс.

Таким образом, в режиме модуляции добротности, лазер излучает наносекундные импульсы с высокой пиковой мощностью, достигающей сотен мегаватт

[4,13,14].

9.4.4.Синх ронизация мод в твердотельном лазере и

генерация ультракоротких импульсов (УКИ)

Обычно, твердотельные лазеры генерируют на достаточно большом числе типов колебаний (мод). При этом, однако, фазовая связь между полями различных мод отсутствует. Усложнением схемы генератора можно добиться жесткой связи между фазами колебаний мод. В таком случае говорят, что генератор работает в режиме синхронизации мод. Если связь между фазами мод устанавливается самопроизвольно, то говорят что, имеет место самосинхронизация мод.

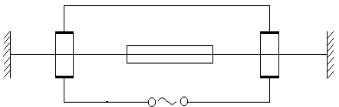
При появлении синхронизации мод, временные характеристики лазеров резко меняются. Чтобы понять происходящие изменения, рассмотрим схему лазера бегущей волны (рис. 9.6).

247

Рис. 9.6. Схема лазера бегущей волны с синхронизацией мод:

1 – зеркала; 2 – активный элемент; 3 – модулятор

В резонаторе такого генератора поле может быть представлено в виде суммы волн, бегущих со скоростью света в каком-то направлении, например, по часовой стрелке. Для простоты будем полагать, что этих типов колебаний всего два

E1= Em×sin(w0×t – k0×x )

E2= Em×sin(w1×t – k1×x ) ,

где k0, 1 = w0, 1 / c -– волновое число; w0, 1 – частота типов колебаний.

Расстояние между ними по частоте w1= 2p×с/ L совпадает с расстоянием между продольными модами. Соответственно волновые числа волн отличаются на k1= 2 p / L , где L – полная длина резонатора.

Примем также, что амплитуды волн равны, а фазы колебаний в момент времени t = 0 в точке z= 0 совпадают и далее жестко между собой связаны. Тогда поле в точке z в момент времени t будет

Отсюда видно, что произведение сомножителей перед последним синусом может быть взято за амплитуду поля, медленно меняющуюся во времени и пространстве. Интенсивность света I пропорциональна квадрату амплитуды поля, так что из (9.29) получим

График зависимости I(z,t) представлен на рис.9.7. Как видно, распределение поля неравномерно, причем поле в интервале L/2 превышает среднее значение и в таком же интервале оно меньше среднего. Вся картина поля не остается неизменной в пространстве, а перемещается вдоль оси резонатора z со скоростью света c=w1/k1. В некоторый момент времени максимум интенсивности света набегает на выходное зеркало. В этот момент через зеркало проходит максимальная мощность излучения. Через промежуток времени 2L/ c у зеркала окажется минимум интенсивности. При этом мощность излучения минимальна. Вывод: при синхронизации двух типов колебаний интенсивность выходного излучения является периодической функцией времени с периодом 2L/c.

248

Рис. 9.7. Распределение интенсивности поля в резонаторе

при синхронизации двух типов колебаний

Качественно эта картина остается верной и при синхронизации большого числа мод. Однако распределение интенсивности света в резонаторе гораздо более неравномерно, чем при двух синхронизованных модах. Амплитуда результирующего поля при синхронизации типов колебаний отлична от нуля в интервале 2L/N (N – число синхронизованных мод). На остальной части резонатора поле близко к нулю (рис.9.8).

Рис. 9 8. Распределение поля в резонаторе лазера

при синхронизации N мод

Максимум поля по-прежнему перемещается в направлении оси резонатора со скоростью света. Каждый раз, когда максимум интенсивности оказывается у выходного зеркала, генератор излучает импульс света.

Таким образом, в режиме синхронизации мод лазер выдает импульс света с периодом повторения T= 2L/ c и длительностью импульсов τ = T/ N . Если 2L=1м,

то Fповт=1/ T= 300 МГц, а τ при синхронизации 100 мод будет 3×10–11 с. Пиковая мощность превышает среднюю в (T/ τ)=100 раз.

Переход к генерации с синхронизацией мод может быть осуществлен с помощью модулятора потерь, помещенного в резонатор лазера. Если коэффициент пропускания этого модулятора изменяется с частотой Fповт= c/2L, то при отсутствии синхронизации мод, потери энергии в модуляторе будут пропорциональны среднему за период коэффициенту пропускания модулятора.

При синхронизации типов колебаний формируется импульс, который может проходить через модулятор как раз в те моменты времени, когда потери в модуля-

249

торе малы. В результате режим с синхронизацией мод оказывается энергетически более выгодным и, следовательно, в схеме, представленной на рис.9.8 он разовьется в первую очередь. Могут быть и другие схемы получения режима синхронизации мод.

В настоящее время в режиме синхронизации типов колебаний могут быть получены импульсы света с длительностью, измеряемой долями пс и пиковой мощностью 1011 Вт (число синхронизированных мод ограниченно, так как это зависит от многих факторов [4].

9.4.5. Спектральные и угловые характеристики твердотельных лазеров

Хотя излучение лазера обладает на несколько порядков меньшей шириной спектра (чем тепловые источники) полностью монохроматичным назвать нельзя. Например, в рубиновом лазере, если не принять специальные меры Dּν= 30 ГГц, т.е. 5×10–5 от ν0. Для многих приложений это недопустимо. Кроме того, наряду с нерегулярным во времени излучением (“ пичками”) наблюдается также нерегулярное изменение спектра – в генерацию входят в разных “ пичках” различные продольные моды. Разберем причины нерегулярности спектра излучения лазера во времени.

Вначале генерация лазера развивается на том аксиальном типе колебаний, который расположен наиболее близко к центру линии люминесценции и, следовательно, обладает большим усилением. По мере возрастания амплитуды поля этого колебания, разность населений рабочих уровней будет падать, а с ней и коэффициент усиления. Однако, поскольку поле аксиальной моды представляет собой стоячие волны, разность населенностей будет падать в основном вблизи пучностей стоячей волны (см. рис.9.9).

Рис. 9.9. Распределение поля аксиальной моды в резонаторе

Высвечивание активных ионов в минимумах очевидно не происходит. Это благоприятствует возбуждению тех мод, пучности которых расположены в области узлов основной моды. Таким образом, происходит срыв генерации одной моды (или группы мод) и в генерацию входят другие моды.

Расчеты показывают, что за счет неоднородности распределения поля мод, генерация происходит на многих модах в частотном интервале

250

Как видно из (9.31), ширина спектра генерации Dν зависит от уровня накачки. На пороге генерации a ® 1 и Dν ® 0. При повышении уровня накачки Dν растет, очень быстро достигая насыщения ν пред при a ®0. Это предельное значе-

Оценим Dνпред.. При длине резонатора L = 0,5 м - dν = c/ 2L= 300 МГц,

пусть далее Dνл= 300 ГГц, тогда Dνпред » 20 ГГц, что согласуется с экспериментальными результатами.

Из изложенного следует, что устранение продольной неоднородности поля мод, должно приводить к сужению спектра излучения лазера.

Устранение неоднородности взаимодействия вещества и поля можно достичь различными способами, например, двигая активный элемент вдоль оси резонатора в процессе генерации, или двигая поле в активном элементе с помощью электрооптических кристаллов, помещенных в оптический резонатор (рис. 9.10).

Рис. 9.10. К иллюстрации устранения неоднородностей с помощью двух электрооптических кристаллов

Впоследнем случае, электрическое поле изменяет скорость распространения света в кристаллах, поэтому меняется l = υ/ ν = c/ ν π, и при изменении напряжения стоячая волна двигается в активном элементе. Важным является также то, что

втаких лазерах происходит не только сужение спектра генерации, но и улучшение ее кинетики. Последовательность пичков приобретает хорошую регулярность.

Существенно зависят спектральные и временные характеристики лазера от сферичности зеркал резонатора. При достаточно большой сферичности в генерацию вовлекается большое число поперечных мод. Когда имеет место сильное перекрытие спектров мод с различными аксиальными индексами, последовательность пичков регуляризуется, спектр сужается. Но угловая расcходимость излучения при этом возрастает. Использованием различных методов сужения спектра излучения лазера можно добиться его ширины до нескольких десятков МГц.

Взаключении раздела отметим, что в твердотельных лазерах (при генерации многих поперечных мод) угловая расcходимость излучения значительно превы-

шает дифракционную (она составляет (1¸5)×10–3 рад.). Предельное значение угловой расcходимости при выходе в генерацию многих поперечных мод и при высоком уровне накачки, можно оценить по формуле [4].

αпред @ 0.7×[ln( 1/ r)]1/ 3×[ l/ d]1/ 3, (9.33)

где r – коэффициент отражения выходного зеркала, d – диаметр активного элемента.