
Нечеткая логика и нейронные cети
..pdf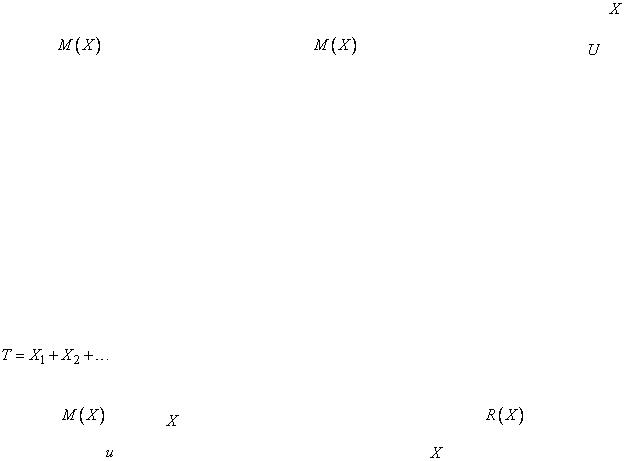
|
|
|
41 |
правило, ставящее в соответствие |
каждой нечеткой переменной |
ее |
|
смысл |
, (нечеткое подмножество |
универсального множества |
). |
Конкретное название 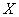 , порожденное синтаксическим правилом
, порожденное синтаксическим правилом 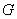 ,
,
называется термом. Терм, состоящий из одного слова или нескольких слов,
всегда фигурирующих вместе друг с другом, называется атомарным термом.
Терм, состоящий из одного или более атомарных термов, называется составным термом. Конкатенация некоторых компонент составного терма является подтермом. Если  — термы в
— термы в 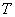 , то
, то 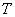 можно представить в виде объединения
можно представить в виде объединения
Смысл |
терма определяется как ограничение |
на базовую |
переменную , обусловленное нечеткой переменной : |
|
|
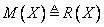 ,
,
имея в виду, что 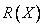 и, следовательно,
и, следовательно,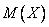 можно рассматривать как нечеткое подмножество множества
можно рассматривать как нечеткое подмножество множества 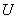 , имеющее название
, имеющее название 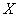 . Связь между ее лингвистическим значением и базовой переменной показана на рис. 1.2.3.
. Связь между ее лингвистическим значением и базовой переменной показана на рис. 1.2.3.
Лингвистическое значение включает связки, такие, как “и, или, ..., ни и т. п.;
отрицание не; неопределенности, как очень, более или менее, совершенно,
совсем, безусловно, чрезвычайно, отчасти и т. п”. Связки, неопределенности и отрицание можно трактовать как операторы, видоизменяющие смысл первичных термов особым образом.
42
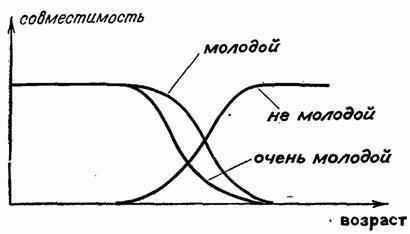
Если функция принадлежности лингвистического значения “молодой” изображается кривой, показанной на рис. 1.2.4, то смысл лингвистического значения “очень молодой” получается возведением в квадрат значений функции совместимости лингвистического значения молодой. Смысл лингвистического значения “не молодой” можно получить, вычитая из 1 значения этой функции
совместимости (рис. 1.2.4).
Рис. 1.2.4. Функции совместимости значений “молодой, не молодой, очень молодой”.
Лингвистическая переменная “Возраст” является по своей природе числовой переменной. Смысл лингвистического значения, такого, как молодой,
определяется функцией принадлежности, ставящей в соответствие каждому значению базовой переменной из интервала 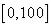 число из интервала
число из интервала 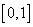 ,
,
представляющее принадлежность данного возраста с понятием “молодой”.
Лингвистическая переменная “Внешность” не имеет четко определенной базовой переменной. Степень красоты с помощью физических величин трудно выразить. В этом случае каждой женщине приписывается степень принадлежности классу прекрасных женщин, например Фэй - степень 0.9,
Адели - 0.7, Кетти - 0.8 и Вере - 0.9. Но эти значения функции принадлежности основаны лишь на впечатлениях, которые точно не формализуются.
43
Базовая переменная - численная по природе. Лингвистическими перемен-ными
можно оперировать путем использования принципа обобщения для нечетких множеств. Для красоты способ обращения с лингвистическими переменными носит качественный характер. Поскольку присутствуют вычисления,
лингвистический подход не является по своей природе целиком качественным,
а имеет соответствующие вычисления.
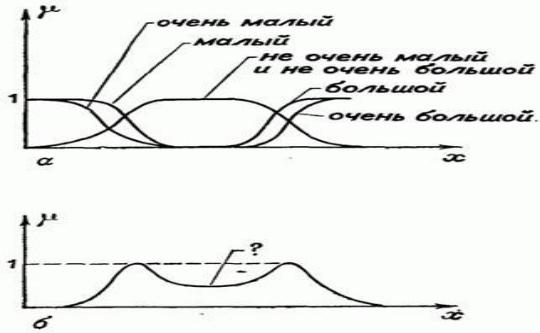
Рис. 1.2.5. а. Функции принадлежности значений малый, очень малый, большой,
очень большой и не очень малый и не очень большой. б.
Лингвистическое приближение представляет задачу нахождения приближенного лингвистического описания функции принадлежности.
Поэтому лингвистическая переменная представляет область приближенных рассуждений.
Нечеткую переменную можно представить сумкой с мягкими стенками
(Рис.1.2.6). Если лингвистическая переменная определяется как переменная,
значениями которой являются нечеткие переменные, то лингвистическая переменная представляется в виде твердой сумки, в которую можно поместить
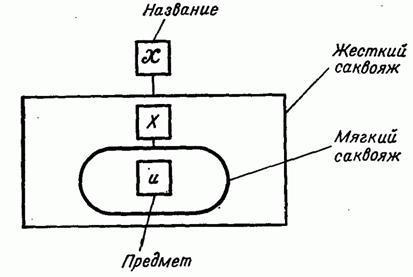
44
мягкие сумки с ярлыками. На каждом из этих ярлыков приведено описание нечеткого ограничения на множество предметов, которые можно поместить в соответствующую мягкую сумку.
Рис. 1.2.6 Аналогия с саквояжем для лингвистической переменной
1.3. Функции принадлежности
Нечеткие множества описывают расплывчатые понятия человеческого языка и для этого характеризуются функцией принадлежности. На практике функция принадлежности задается вне самой задачи и, ее адекватность не может быть проверена теоретически. Поэтому в каждом методе построения функции принадлежности формулируются свои требования и обоснования.
Функция принадлежности приписывает каждому элементу 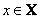 степень его принадлежности к нечеткому множеству
степень его принадлежности к нечеткому множеству 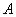 , при этом возможны три варианта:
, при этом возможны три варианта:
1) 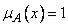 означает полную принадлежность элемента
означает полную принадлежность элемента 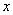 к нечеткому множеству
к нечеткому множеству 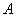 , т.е.
, т.е. 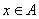 ;
;
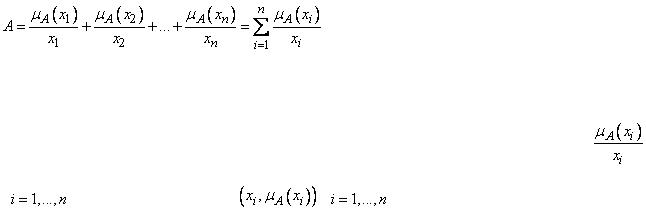
45
2) 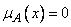 означает отсутствие принадлежности элемента
означает отсутствие принадлежности элемента 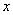 к нечеткому множеству
к нечеткому множеству 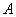 , т.е.
, т.е.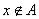 ;
;
3) 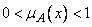 означает частичную принадлежность элемента
означает частичную принадлежность элемента 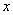 к нечеткому множеству
к нечеткому множеству 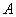 .
.
Если 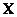 - это пространство с конечным количеством элементов, т.е.
- это пространство с конечным количеством элементов, т.е. 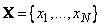 , то нечеткое множество
, то нечеткое множество 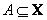 представляется, как
представляется, как
. (1.14)
Эта запись имеет символьный характер и означает приписывание конкретным
элементам 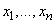 степеней принадлежности
степеней принадлежности 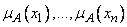 . Запись
. Запись
, |
означает пару |
, |
. |
(1.14) |
Функций принадлежности определяется следующими условиями:
1.Функция принадлежности должна быть положительной,
т.е. μ А i (x)>0.
2.Функция принадлежности должна быть нормальной
Sup μ А i x = 1.
Если условие нормальности принято, то запрещается использование функций принадлежности, не удовлетворяющих этому условию.
46
Рис. 1.3.1. Нормальные (1,2) и запрещенные (3) функции принадлежности
3. В базовом множестве термов Т запрещается использование пар термов,
представленных рис. (1.3.2. а, б). В первом случае отсутствует разделение понятий, представленных соседними термами τi u τi+1, во втором - участку [c, d]
из области определения не поставлено в соответствие какоелибо понятие.
Рис. 1.3.2. Пары термов запрещенные к использованию
4. Термы с минимальными и максимальными номерами не должны соответ-
ствовать колоколообразным функциям принадлежности. Для этих термов функции принадлежности имеют S-образный вид
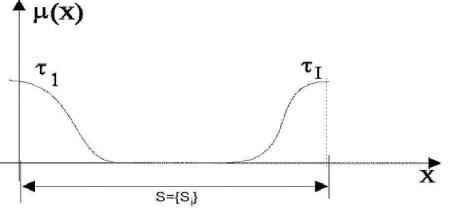
47
Рис. 1.3.3. Функция принадлежности для термов с минимальными и макси-
мальными номерами
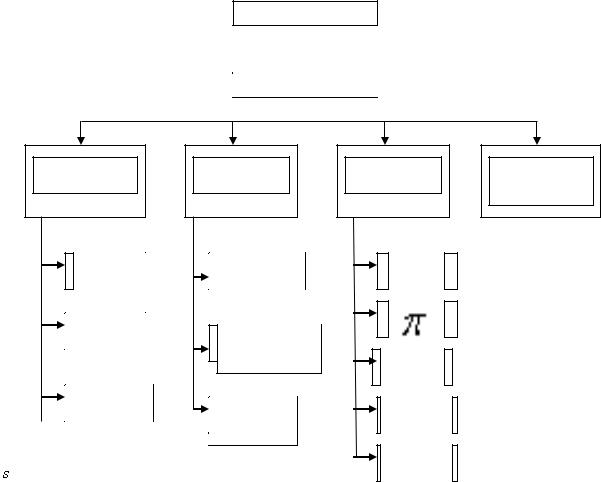
Можно выделить следующие способы здания функций принадлежности (Рис.
1.3.4.)
-прямые
-косвенные
-типовые формы
-по результатам эксперимента
В прямых методах эксперт просто задает правила определения значений функции принадлежности μA множества A. Эти значения согласуются с его предпочтениями на множестве U.
Целесообразность прямых методов обосновывается в [4]: «По своей природе оценка является приближением. Во многих случаях не требуется высокая точность. Человеческий мозг использует допустимость такой неточности, кодируя информацию элементами нечетких множеств/ Поток информации, поступающий в мозг через органы зрения, слуха, осязания и др.,
сжимается в тонкую струйку информации, необходимой для решения поставленной задачи с минимальной степенью точности».
48
Прямые методы, основанные на непосредственном определении функции принадлежности, используются в случае, когда эксперты свободны от случайных ошибок и работают как «надежные и правильные приборы».
Способы
задания
функций
прямые |
косвенн |
осн.типы |
по |
|
|
|
резуль- |
табл |
1 эксперт |
S |
|
форму |
Группа |
|
|
|
|
|
|
|
экспертов |
y |
|
графики |
Парное |
t |
|
|
|
||
|
сравнеи |
|
|
|
|
L |
|
Рис. 1.3.4. Классификация способов построения функций принадлежности
Примеры прямых методов: непосредственное задание μA таблицей, формулой,
графиком. Прямые методы задания функции принадлежности используются для измеримых величин, таких как скорость, время, расстояние, давление,
температура и т. д., или когда выделяются полярные значения.
Во многих задачах при характеристике объекта можно выделить набор признаков и для каждого из них определить полярные значения,
49
соответствующие значениям функции принадлежности, 0 или 1. При этом
используют следующую процедуру:
–определить список свойств, по которым оценивается объект;
–найти в этом списке полярные свойства и сформировать полярную шкалу;
–для каждой пары полюсов оценить, как сильно он обладает этим свойством.
Например, в задаче распознавания лиц можно выделить следующие шкалы:
|
Признаки |
0 |
1 |
Xl |
Высота лба |
Низкий |
Широкий |
Х2 |
Профиль носа |
Курносый |
Горбатый |
Х |
Длина носа |
Короткий |
Длинный |
|
|||
Х4 |
Разрез глаз |
Узкие |
Широкие |
Х5 |
Цвет глаз |
Светлые |
Темные |
Х6 |
Форма |
Остроконечный |
Квадратный |
X |
Толщина губ |
Тонкие |
Толстые |
Х8 |
Цвет лица |
Темный |
Светлый |
X |
Очертание лица |
Овальное |
Квадратное |
Для конкретного лица A эксперт, исходя из приведенной шкалы, задает
µA (х) € [0,1], формируя векторную функцию принадлежности µA (х 1), µA (х2),
…,µА (х9)}.
Также используются прямые методы для группы экспертов, когда, например,
группе экспертов предъявляют конкретное лицо, и каждый должен дать один из двух ответов: «этот человек лысый» или «этот человек не лысый», тогда количество утвердительных ответов, деленное на общее число экспертов, дает значение µ «лысый» (данного лица).
Допустим, что 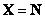 - множество натуральных чисел. Определим понятие множества натуральных чисел, «близких числу 7». Это можно сделать определением следующего нечеткого множества
- множество натуральных чисел. Определим понятие множества натуральных чисел, «близких числу 7». Это можно сделать определением следующего нечеткого множества 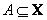 :
:
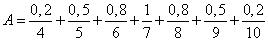 .
.
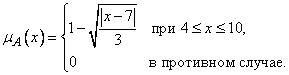
50
Если 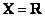 , где
, где 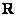 - множество действительных чисел, то множество действительных чисел, «близких числу 7», можно определить функцией принадлежности вида
- множество действительных чисел, то множество действительных чисел, «близких числу 7», можно определить функцией принадлежности вида
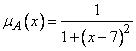 . (1.15)
. (1.15)
Поэтому нечеткое множество действительных чисел, «близких числу 7»,
описывается выражением
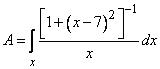 .
.
Нечеткие множества натуральных или действительных чисел, «близких числу
7», можно записать различными способами. Например, функцию принадлежности (3.10) можно заменить выражением
(1.16)
На рис. 1.3.1 а и б представлены две функции принадлежности нечеткого множества  действительных чисел, «близких числу 7».
действительных чисел, «близких числу 7».
