
Нечеткая логика и нейронные cети
..pdf211
числе и не представленных при обучении, называется свойством обобщения нейронной сети.
Для настройки параметров нейронных сетей широко используется также процедура адаптации, когда подбираются веса и смещения с использованием произвольных функций их настройки, обеспечивающие соответствие между входами и желаемыми значениями на выходе.
Методы определения экстремума функции нескольких переменных делятся на три категории – методы нулевого, первого и второго порядка:
методы нулевого порядка, в которых для нахождения экстремума используется только информация о значениях функции в заданных точках;
методы первого порядка, где для нахождения экстремума используется градиент функционала ошибки по настраиваемым параметрам;
методы второго порядка, вычисляющие матрицу вторых производных функционала ошибки (матрицу Гессе).
Кроме перечисленных методов можно выделить также стохастические алгоритмы оптимизации и алгоритмы глобальной оптимизации, перебирающие значения аргументов функции ошибки.
Правило обучения Хебба
Правила обучения Хебба относятся к ассоциативным обучающим правилам.
Согласно правилу Хебба обучение сети происходит в результате усиления силы связи между одновременно активными элементами, его можно определить так:
wij (t 1) wij (t) xi y j , |
(3.6) |
где t – время, xi, yj – соответственно выходные значения i-го и j-го нейронов, -
скорость обучения равна 1. В начальный момент предполагается, что wij(0)=0
для всех i и j. Правило Хебба можно использовать как при обучении с учителем, так и без него. Если в качестве выходных значений сети
212
используются целевые значения, тогда реализуется обучение с учителем. При использовании в качестве y реальных значений, которые получаются при подаче входных образов на вход сети, правило Хебба соответствует обучению без учителя. В этом случае коэффициенты сети в начальный момент времени инициализируются случайным образом. Обучение заканчивается после подачи всех имеющихся входных образов на нейронную сеть. В общем случае это правило не гарантирует сходимости процедуры обучения сети.
Требуется реализовать обучение нейронной сети по правилу Хебба с учителем для операции «логическое И», используя биполярную кодировку двоичных сигналов.
Общее количество входных образов, подаваемых на нейронную сеть, L=4.
Правило Хебба в случае сети с тремя нейронами на входе и одним на выходе реализуется по формулам:
w11(t 1) w11(t) x1 y,
w21(t 1) w21(t) x2 y, (3.7)
S0 (t 1) S0 (t) y.
Обучение с учителем для «логического И» соответствует данным,
приведенным в табл. 1.
Таблица 1
Результаты обучения сети по правилу Хебба
X1 |
X2 |
X3=S0 |
Y |
W11 |
W21 |
S0 |
|
|
|
|
|
|
|
-1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
1 |
-1 |
-1 |
-1 |
0 |
2 |
2 |
|
|
|
|
|
|
|
-1 |
1 |
-1 |
-1 |
1 |
1 |
3 |
|
|
|
|
|
|
|
1 |
1 |
-1 |
1 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
213 |
Эта таблица формируется по строкам. Считая S0 (0)=0, начальные w(0) |
0 , |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
w |
(0) |
0, |
|
для |
|
|
четырех |
входных образов |
получаем |
|
|||||||
|
|
|
|
|
|
||||||||||||
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
последовательно следующие значения для первого образа |
|
||||||||||||||||
w |
(1) |
(0) |
|
x |
|
y 0 ( 1) ( 1) 1, |
|
|
|||||||||
|
|
w |
|
|
|
|
|
|
|
||||||||
|
11 |
11 |
|
1 |
|
|
|
|
|
|
|
|
|||||
w |
(1) |
(0) |
|
x |
|
y 0 ( 1) ( 1) 1, |
|
|
|||||||||
|
|
w |
|
|
|
|
|
|
|
||||||||
|
21 |
21 |
|
2 |
|
|
|
|
|
|
|
||||||
S (1) S |
|
(0) y 0 ( 1) 1; |
|
|
|
||||||||||||
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||
для второго |
|
|
|
|
|
|
|
|
|||||||||
w |
(2) |
w |
|
(1) |
x |
|
|
y 1 1 ( 1) 0, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
11 |
11 |
|
1 |
|
|
|
|
|
|
|||||||
w |
(2) |
w |
|
(1) |
x |
|
|
y 1 ( 1) ( 1) 2, |
|
|
|||||||
21 |
21 |
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
S |
0 |
(2) S |
0 |
(1) y 1 ( 1) 2; |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
для третьего |
|
|
|
|
|
|
|
|
|||||||||
w |
(3) |
w |
(2) |
x |
|
y 0 ( 1) ( 1) 1, |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
11 |
11 |
|
|
1 |
|
|
|
|
|
|
||||||
w |
(3) |
w |
(2) |
x |
|
y 2 1 ( 1) |
1, |
|
|
||||||||
21 |
21 |
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
S |
0 |
(3) S |
0 |
(2) y 2 ( 1) 3; |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и для четвертого образа |
|
|
|
|
|||||||||||||
w |
(4) |
w |
|
(3) |
x |
|
y 1 1 1 2, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
11 |
11 |
|
|
1 |
|
|
|
|
|
|
||||||
w |
(4) |
w |
|
(3) |
x |
|
y |
1 1 1 2, |
|
|
|
||||||
21 |
21 |
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
S |
0 |
(4) S |
0 |
(3) y 3 1 2. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Таким образом, в результате обучения получается уравнение разделяющей |
|||||||||||||
линии для операции «логическое И», представленной ранее на рис. 3.2.6: |
|
||||||||||||||||
2 x1 2 x2 2 0 , |
или |
x2=1-x1 . |
|
|
|||||||||||||
|
|
|
|
Правило обучения по Хеббу в общем случае задается формулой: |
|
||||||||||||
wij (t 1) wij (t) xi y j , |
i=1,2,…,L, |
j=1,2,…,p, |
|
||||||||||||||

214
где – коэффициент обучения или темп обучения, в нейроимитаторе NNT это правило реализует процедура настройки learnh. Правило Хебба с модификацией весов определяется по формуле:
wij (t 1) wij (t) xi y j wij (t),
где – коэффициент убывания или возрастания веса.
Для решения задачи «исключающего ИЛИ» можно использовать сеть второго
порядка, |
включающую произведение переменных, тогда взвешенная сумма |
S 2 x1 |
2 x2 4 x1 x2 1. (Рис.3.2.7) |
Правило обучения перцептрона
Персептрон – нейронная сеть прямой передачи сигнала с бинарными входами и бинарной пороговой функцией активации.
Правило обучения Розенблатта в общем случае является вариантом правил обучения Хебба, формирующих симметричную матрицу связей, и в тех же обозначениях имеет вид:
w |
(t 1) w |
(t) (t |
i |
y |
j |
) x |
, |
ij |
ij |
|
|
i |
|
(3.8)
где – коэффициент обучения, 0<<1, tj – эталонные или целевые значения.
Правило обучения персептрона с нормализацией используется тогда, когда имеется большой разброс в значениях компонент входного вектора. Тогда каждая компонента делится на длину вектора:
x |
' |
|
|
|
xi |
, |
|
i |
|
|
|
|
|||
|
x |
2 |
x |
2 |
x |
2 |
|
|
|
||||||
|
|
|
2 |
n |
|||
|
|
1 |
|
|
|||
i=1,2,…,n.
Алгоритм обучения Розенблата:
1.Весовые коэффициенты сети инициализируются случайным образом или устанавливаются нулевыми.
2.На вход сети поочередно подаются входные образы из обучающей выборки,
которые затем преобразуются в выходные сигналы Y.
215
3.Если реакция нейронной сети yj совпадает с эталонным значением tj, то весовой коэффициент wij не изменяется.
4.Если выходное значение не совпадает с эталонным значением, то есть yj не равно tj, то производится модификация весовых коэффициентов wij по соответствующей формуле.
5.Алгоритм повторяется до тех пор, пока для всех входных образов не будет
достигнуто совпадение с целевыми значениями или не перестанут
изменяться весовые коэффициенты.
Линейная разделяющая поверхность, формируемая персептроном, позволяет решать ограниченный круг задач.
Правило обучение Видроу - Хоффа
Правило Видроу – Хоффа используется для обучения сети, состоящей из слоя распределительных нейронов и одного выходного нейрона с линейной функцией активации. Такая сеть называется адаптивным нейронным элементом (Adaptive Linear Element) или «ADALINE». Выходное значение такой сети определяется по формуле
|
n |
|
|
|
|
|
y |
|
w |
x |
i |
S |
0 |
|
i1 |
|
|
|||
|
i 1 |
|
|
|
|
|
,
где n – число нейронов распределительного слоя, S0 – смещение.
Правило обучения Видроу – Хоффа известно под названием дельта-правила
(delta-rule). Оно предполагает минимизацию среднеквадратичной ошибки нейронной сети, которая для L входных образов определяется следующим образом:
|
1 |
L |
2 |
|
|
|
|
|
|||
E |
y (k ) t (k ) , |
(3.9) |
|||
2 |
|||||
|
k 1 |
|
|
||

216
где y(k) и t(k) – выходное и целевое значения сети соответственно для k-го образа.
Правило Видроу – Хоффа базируется на методе градиентного спуска в пространстве весовых коэффициентов и смещений нейронной сети. По этому методу веса и смещения изменяются с течением времени следующим образом:
w |
(t 1) |
i1 |
|
w |
(t)-α |
i1 |
|
E(k) |
|
w |
(t) |
i1 |
|
,
S |
0 |
(t 1) |
|
|
|
|
S |
|
(t) |
E(k) |
||
0 |
S |
|
(t) |
||
|
|
|
|||
|
|
|
0 |
||
|
|
|
|
|
|
, i=1,2,…,n,
где – скорость обучения, 0<<1.
Вычислим частные производные:
E(k) |
|
|
E(k) |
|
y |
(k ) |
|
|||||||
|
|
|
|
( y |
||||||||||
w |
|
y |
(k ) |
|
w |
|
|
|
||||||
(t) |
|
|
|
|
|
(t) |
||||||||
|
|
|
|
|
|
|||||||||
i1 |
|
|
|
|
|
|
|
i1 |
|
|
||||
E(k) |
|
E(k) |
|
|
y |
(k ) |
|
|||||||
|
|
|
|
|
|
|
( y |
|||||||
(t) |
|
y |
(k ) |
|
S0 |
(t) |
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(k )
(k )
t
t
(k )
(k )
)
)
,
x(k ) i
,
|
|
|
(k ) |
– i-я компонента |
|||||
где xi |
|||||||||
w |
|
(t 1) w |
|
(t) ( y |
( |
||||
|
|
|
|||||||
|
i1 |
|
|
i1 |
|
|
|
||
S |
|
(t 1) S |
|
(t) ( y |
(k |
||||
0 |
0 |
|
|
||||||
|
|
|
|
|
|
|
|
||
k-го образа. По дельта-правилу
k ) |
t |
(k ) |
) x |
(k ) |
, |
|||
|
|
|
|
i |
||||
|
|
|
|
|
|
|
|
|
) |
t |
(k ) |
), |
|
i 1,2,...,n. |
|||
|
|
|
|
|||||
Выражение для пересчета весов сети эквивалентно правилу обучения Розенблатта, если на выходе линейного адаптивного элемента использовать пороговый элемент. Видроу и Хофф доказали, что минимизация среднеквадратичной ошибки сети производится независимо от начальных значений весовых коэффициентов. Суммарная среднеквадратичная ошибка сети
E должна достигнуть заданного минимального значения Emin. Для алгоритма Видроу – Хоффа рекомендуется выбирать значение скорости обучения по
следующему правилу: (l) 1l , где l – номер итерации в алгоритме обучения.
Адаптивный шаг обучения для линейной нейронной сети позволяет повысить скорость обучения и определяется по формуле [2]:
217
(t) |
1 |
. |
|
|
|||
n |
|||
|
|
||
|
1 xi2 (t) |
|
|
|
i 1 |
|
Способ обучения с обратным распространением ошибки
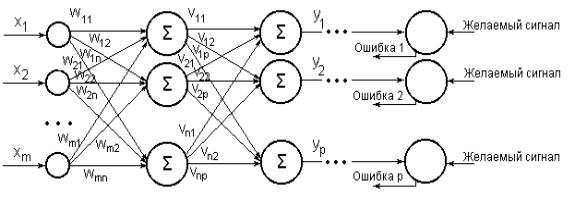
Этот способ обратного распространения ошибки предложен несколькими авторами независимо в 1986 г. для многослойных сетей с прямой передачей сигнала. Многослойная нейронная сеть способна осуществлять любое отображение входных векторов в выходные (рис. 3 . 5 . 1 )
Р и с . 3 . 5 . 1 . Многослойная сеть со скрытым слоем из n нейронов
Входной слой нейронной сети выполняет распределительные функции.
Выходной слой нейронов служит для обработки информации от предыдущих слоев и выдачи результатов. Слои нейронных элементов, расположенные между входным и выходным слоями, называются скрытыми. Как и выходной слой,
скрытые слои являются обрабатывающими. Выход каждого нейрона предыдущего слоя сети соединен синаптическими связями со всеми входами нейронных элементов следующего слоя. В качестве функций активации в многослойных сетях чаще других используются сигмоидальные функция и гиперболический тангенс. Метод обратного распространения ошибки минимизирует среднеквадратичную ошибку нейронной сети, при этом

218
используется метод градиентного спуска в пространстве весовых коэффициентов и смещений нейронных сетей. Согласно методу градиентного спуска по поверхности ошибок изменение весовых коэффициентов и смещений сети осуществляется по формулам:
w (t 1) w (t) |
E(k) |
, |
|||||||||
|
|||||||||||
|
ij |
ij |
|
|
wij |
(t) |
|||||
|
|
|
|
|
|
||||||
S |
|
(t 1) S |
|
(t) |
|
E(k) |
|||||
0 j |
0 j |
S |
|
|
(t) |
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0 j |
||||
|
|
|
|
|
|
|
|
|
|
||
,
(3.10)
i=1,2,…,n; j=1,2,…,p,
где E – среднеквадратичная ошибка сети для одного из k образов,
определяемая по формуле
|
1 |
p |
|
E |
( y j |
||
|
|||
|
2 j 1 |
||
t |
|
) |
2 |
j |
|
||
|
|
|
,
здесь tj – желаемое или целевое выходное значение j-го нейрона.
Ошибка j-го нейрона выходного слоя равна: j = yj – tj.
Для любого скрытого слоя ошибка i-го нейронного элемента определяется рекурсивно через ошибки нейронов следующего слоя j:
i
m j j 1
F ' (S |
j |
) w |
|
ij |
,
где m – количество нейронов следующего слоя по отношению к слою i, wij – вес или синаптическая связь между i-ым и j-ым нейронами разных слоев, Sj –
взвешенная сумма j-го нейрона.
Весовые коэффициенты и смещения нейронных элементов с течением времени изменяются следующим образом:
wij (t 1) wij (t) j F' (S j ) yi , |
|
S0 j (t 1) S0 j (t) j F' (S j ), |
i=1,2,…,n, j=1,2,…,p, |
219
где – скорость обучения. Это правило называется обобщенным дельта-
правилом. Для сигмоидальной функции активации:
w |
(t 1) w |
(t) |
j |
y |
j |
(1 y |
j |
) y |
i |
||
ij |
|
ij |
|
|
|
|
|
||||
S0 j (t 1) |
S0 j (t) j y j (1 y j ) , |
i=1,2,…,n, j=1,2,…,p, |
|||||||||
ошибка j-го нейрона выходного слоя определяется как
j = y j – tj,
а j-го нейрона скрытого слоя
m
К
m |
|
j j yi (1 |
yi ) wij , где |
i 1 |
|
– количество нейронов следующего слоя по отношению к слою j.
недостаткам метода обратного распространения ошибки относят следующие:
медленную сходимость градиентного метода при постоянном шаге обучения;
возможное смешение точек локального и глобального минимумов;
влияние случайной инициализации весовых коэффициентов на скорость поиска минимума.
Для их преодоления предложено несколько модификаций алгоритма обратного распространения ошибки:
1) с импульсом, позволяющим учесть текущий и предыдущий градиенты
(метод тяжелого шарика), изменение веса тогда:
wij (t 1) j F' (S j ) yi wij (t) ,
где – коэффициент скорости обучения, – импульс или момент, обычно
0< <1, 0,9;
2) с адаптивным шагом обучения, изменяющимся по формуле

220
(t) |
1 |
|
1 x |
||
|
2 i
(t)
;
3) с модификацией по Розенбергу, предложенной им для решения задачи преобразования английского печатного текста в качественную речь:
w |
(t 1) (1 ) |
j |
F' (S |
j |
) y |
i |
ij |
|
|
|
wij (t 1) wij (t) wij (t 1) .
wij
(t)
,
Использование производных второго порядка для коррекции весов алгоритма обратного распространения ошибки, как показала практика, не дало значительного улучшения решений прикладных задач.
Для многослойных сетей прямой передачи сигнала с логистической функцией активации рекомендуется случайные начальные значения весов инициализировать по правилу (Р. Палмер)
wij 1 ,
n(i)
где n(i) – количество нейронных элементов в слое i.
По мнению других авторов [2], начальные весовые коэффициенты следует выбирать в диапазоне [-0.05;0.05] или [-0.1;0.1]. При этом смещение S0
принимает единичные значения в начальный момент времени. Кроме этого,
количество нейронных элементов скрытых слоев должно быть меньше тренировочных образов. Для обеспечения требуемой обобщающей способности сети можно использовать сеть с несколькими скрытыми слоями, размерность которых меньше, чем для сети с одним скрытым слоем. Однако нейронные сети,
имеющие несколько скрытых слоев, обучаются значительно медленнее.
Искусственные нейронные сети могут обучаться по существу тем же самым образом посредством случайной коррекции весов. Вначале делаются большие случайные коррекции с сохранением только тех изменений весов, которые
