
Нечеткая логика и нейронные cети
..pdf221
уменьшают целевую функцию. Затем средний размер шага постепенно уменьшается, и глобальный минимум в конце концов достигается.
Обучение нейронных сетей способом отжига
Это напоминает отжиг металла, поэтому для ее описания часто используют термин «имитация отжига». В металле, нагретом до температуры,
превышающей его точку плавления, атомы находятся в сильном беспорядочном движении. Как и во всех физических системах, атомы стремятся к состоянию минимума энергии (единому кристаллу в данном случае), но при высоких температурах энергия атомных движений препятствует этому. В процессе постепенного охлаждения металла возникают все более низкоэнергетические состояния, пока не будет достигнут глобальный минимум. В процессе отжига распределение энергетических уровней описывается следующим соотношением:
P(e) = exp(–e/kT) |
(3.11) |
где Р(е) – вероятность того, что система находится в состоянии с энергией е; k –
постоянная Больцмана; Т – температура по шкале Кельвина.
При высоких температурах Р(е) приближается к единице для всех энергетических состояний. Таким образом, высокоэнергетическое состояние почти столь же вероятно, как и низкоэнергетическое. По мере уменьшения температуры вероятность высокоэнергетических состояний уменьшается по сравнению с низкоэнергетическими. При приближении температуры к нулю становится весьма маловероятным, чтобы система находилась в высокоэнергетическом состоянии.
Алгоритм больцмановского обучения
Этот стохастический метод непосредственно применим к обучению искусственных нейронных сетей:
222
1.Определить переменную Т, представляющую искусственную температуру.
Придать Т большое начальное значение.
2.Предъявить сети множество входов и вычислить выходы и целевую функцию.
3.Дать случайное изменение весу и пересчитать выход сети и изменение целевой функции в соответствии со сделанным изменением веса.
4.Если целевая функция уменьшилась (улучшилась), то сохранить изменение веса.
Если изменение веса приводит к увеличению целевой функции, то вероятность сохранения этого изменения вычисляется с помощью распределения Больцмана:
P(c) = exp(–c/kT) |
(3.12) |
где Р(с) – вероятность изменения с в целевой функции; k – константа,
аналогичная константе Больцмана, выбираемая в зависимости от задачи; Т –
искусственная температура.
Выбирается случайное число r из равномерного распределения от нуля до единицы. Если Р(с) больше, чем r, то изменение сохраняется, в противном случае величина веса возвращается к предыдущему значению.
Система выполняет случайный шаг в направлении, искажающем целевую функцию, позволяя ей тем самым вырываться из локальных минимумов, где любой малый шаг увеличивает целевую функцию.
Для завершения больцмановского обучения повторяют шаги 3 и 4 для каждого из весов сети, постепенно уменьшая температуру Т, пока не будет достигнуто допустимо низкое значение целевой функции. В этот момент предъявляется другой входной вектор, и процесс обучения повторяется. Сеть обучается на всех векторах обучающего множества, с возможным повторением, пока целевая функция не станет допустимой для всех них.

223
Величина случайного изменения веса на шаге 3 может определяться различными способами. Например, подобно тепловой системе весовое изменение w может выбираться в соответствии с гауссовским законом распределения:
P(w) = exp(–w2/T2),
где P(w) – вероятность изменения веса на величину w, Т – искусственная температура.
Скорость уменьшения температуры должна быть обратно пропорциональна логарифму времени, чтобы была достигнута сходимость к глобальному минимуму. Скорость охлаждения в такой системе выражается следующим образом:
|
T |
|
|
T (t) |
0 |
|
|
log(1 |
t) |
||
|
где T(t) – искусственная температура как функция времени; Т0 – начальная искусственная температура; t – искусственное время.
Машины Больцмана часто требуют для обучения очень большого ресурса времени.
Обучение Коши
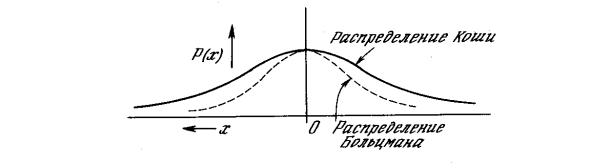
В работе [6] развит метод быстрого обучения подобных систем. В этом методе при вычислении величины шага распределение Больцмана заменяется на распределение Коши. Распределение Коши имеет, как показано на рис.3.4.2
более длинные «хвосты», увеличивая тем самым вероятность больших шагов. В
действительности распределение Коши имеет бесконечную (неопределенную)
дисперсию. С помощью такого простого изменения максимальная скорость уменьшения температуры становится обратно пропорциональной линейной величине, а не логарифму, как для алгоритма обучения Больцмана. Это резко
224
уменьшает время обучения. Эта связь может быть выражена следующим
образом:
T (t) |
T0 |
(3.13) |
||
1 t |
|
|||
Распределение Коши имеет вид |
|
|||
P(x) |
T (t) |
(3.14) |
||
|
||||
T (t)2 x 2 |
||||
где Р(х) есть вероятность шага величины х.
Рис. 3.4.2. Распределение Коши и распределение Больцмана
В уравнении (5.6) Р(х) может быть проинтегрирована стандартными методами.
Решая относительно х, получаем
xc = T(t) tg(P(x)),
где – коэффициент скорости обучения; хc – изменение веса.
Для нахождения х в этом случае (метод Монте Карло) выбирается случайное число из равномерного распределения на открытом интервале (–/2, /2)
(необходимо ограничить функцию тангенса). Оно подставляется в формулу
(5.7) в качестве Р(х), и с помощью текущей температуры вычисляется величина шага.
225
Метод искусственной теплоемкости
Несмотря на улучшение, достигаемое с помощью метода Коши, время обучения может оказаться все еще слишком большим. Способ, уходящий своими корнями в термодинамику, может быть использован для ускорения этого процесса. В
этом методе скорость уменьшения температуры изменяется в соответствии с искусственной «теплоемкостью», вычисляемой в процессе обучения.
Во время отжига металла происходят фазовые переходы, связанные с дискретными изменениями уровней энергии. При каждом фазовом переходе может иметь место резкое изменение величины, называемой теплоемкостью.
Теплоемкость определяется как скорость изменения температуры с энергией.
Изменения теплоемкости происходят из-за попадания системы в локальные энергетические минимумы.
Искусственные нейронные сети проходят аналогичные фазы в процессе обучения. На границе фазового перехода искусственная теплоемкость может скачкообразно измениться. Эта псевдотеплоемкость определяется как средняя скорость изменения температуры с целевой функцией. Сильное начальное возбуждение делает среднюю величину целевой функции фактически не зависящей от малых изменений температуры, т. е. теплоемкость близка к константе. Аналогично при очень низких температурах система останавливается в точке минимума, так что теплоемкость снова близка к константе. Ясно, что в каждой из этих областей допустимы сильные изменения температуры, так как не происходит улучшения целевой функции.
При критических температурах небольшое уменьшение температуры приводит к большому изменению средней величины целевой функции. Средняя величина целевой функции испытывает скачкообразное изменение. В этих критических точках алгоритм должен изменять температуру очень медленно, чтобы гарантировать, что система не окажется случайно в точке, локального минимума. Критическая температура может быть обнаружена по резкому
226
уменьшению искусственной теплоемкости, т. е. средней скорости изменения температуры с целевой функцией. При достижении критической температуры скорость изменения температуры должна замедляться, чтобы гарантировать сходимость к глобальному минимуму. При всех остальных температурах может без риска использоваться более высокая скорость снижения температуры, что приводит к значительному снижению времени обучения.
3.6. Нейронные сети прямого распространения
Персептрон
Модель МакКаллока-Питтса лежит в основе простейшей однонаправленной нейронной сети, названной персептроном. Эту сеть предложил и исследовал Розенблатт в конце пятидесятых - начале шестидесятых годов XX века. На рис.
3.6.1 представлена структура персептрона, иногда называемого простейшим персептроном.
Рис. 3.6.1 Персептрон.
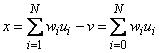
227
В качестве функции 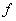 в модели МакКаллока-Питтса (2.2) применялась биполярная функция активации (см.3.3.3).
в модели МакКаллока-Питтса (2.2) применялась биполярная функция активации (см.3.3.3).
Сигнал 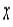 на выходе линейной части персептрона задается выражением
на выходе линейной части персептрона задается выражением
, (3.15)
где 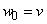 ,
, 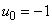 .
.
Задача персептрона заключается в классификации вектора 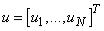 в смысле отнесения его к одному из двух классов, обозначаемых символами
в смысле отнесения его к одному из двух классов, обозначаемых символами 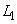 и
и 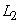 . Персептрон относит вектор
. Персептрон относит вектор 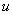 к классу
к классу 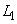 , если выходной сигнал
, если выходной сигнал 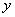 принимает значение 1, и к классу
принимает значение 1, и к классу 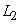 , если выходной сигнал
, если выходной сигнал 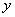 принимает значение
принимает значение 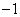 . После этого персептрон разделяет
. После этого персептрон разделяет 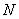 -мерное пространство
-мерное пространство
входных векторов 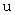 на два полупространства, разделяемые
на два полупространства, разделяемые 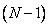 -мерной гиперплоскостью, задаваемой уравнением
-мерной гиперплоскостью, задаваемой уравнением
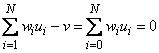 .
.
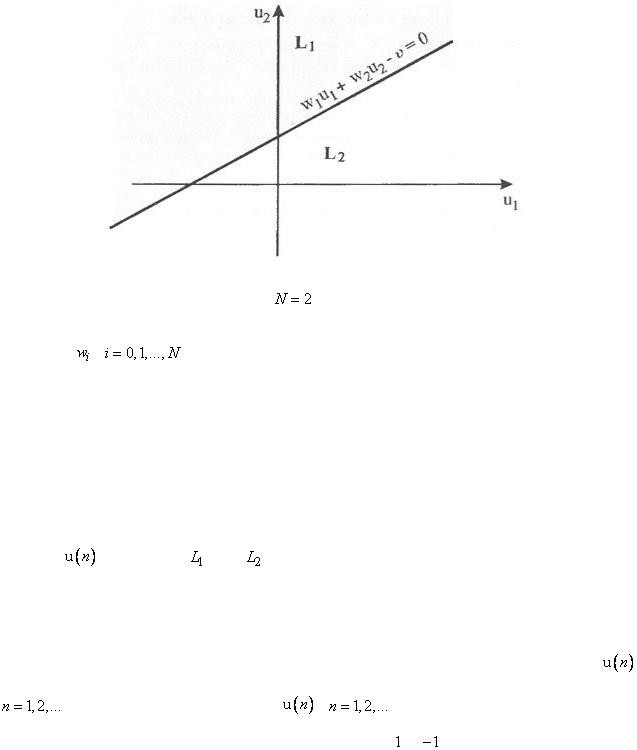
Гиперплоскость (2.9) называется решающей границей. Если 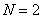 , то решающая граница - это прямая линия, задаваемая уравнением
, то решающая граница - это прямая линия, задаваемая уравнением
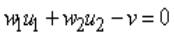 .
.
Точка 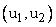 , лежащая над этой прямой (рис. 3.6.2.), относится к классу
, лежащая над этой прямой (рис. 3.6.2.), относится к классу  ,
,
тогда как точка 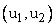 , лежащая под этой прямой, относится к классу
, лежащая под этой прямой, относится к классу 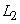 .
.
228
Точки, лежащие на границе решения, можно произвольно отнести и к классу 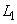 и к классу
и к классу 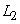 .
.
Рис. 3.6.2. |
Решающая граница для |
. |
|
Если веса |
, |
в уравнении гиперплоскости (2.9) неизвестны, тогда на |
|
вход персептрона последовательно подаются так называемые обучающие сигналы 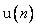 ,
, 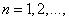 где
где 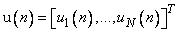 .
.
Неизвестные значения весов будут определяться в процессе обучения
персептрона. |
Роль «учителя» |
заключается в корректном отнесении |
сигналов |
к классам или |
, несмотря на неизвестность весов уравнения |
решающей границы (2.9). По завершении процесса обучения персептрон должен правильно классифицировать поступающие на его вход сигналы, в том
числе |
и |
те, которые отсутствовали в обучающей последовательности |
||||
, |
. |
Множества |
векторов |
, |
, |
для которых выходной |
персептрона принимает соответственно значения |
и |
, линейно отделены, т.е. |
||||
лежат |
в |
двух различных |
полупространствах, разделенных гиперплоскостью |
|||
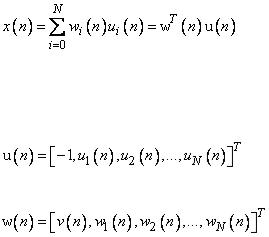
229
(2.9). Другими словами, допускается разделение обучающей последовательности 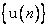 на две последовательности
на две последовательности 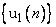 и
и 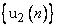 так,
так,
что 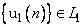 и
и 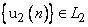 .
.
В 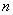 -й момент времени сигнал на выходе линейной части персептрона определяется выражением
-й момент времени сигнал на выходе линейной части персептрона определяется выражением
, |
(3.16) |
где
,
.
Выходной сигнал персептрона может быть описан выражением
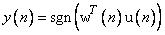 . (3.17)
. (3.17)
С учетом введенных обозначений рекурсии (2.14) и (2.15) принимают вид
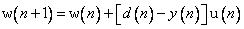 . (3.18)
. (3.18)
Разность 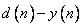 можно интерпретировать как погрешность между эталонным (заданным) сигналом
можно интерпретировать как погрешность между эталонным (заданным) сигналом 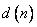 и фактическим выходным сигналом
и фактическим выходным сигналом 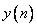 .
.
По завершении обучения решающая граница персептрона определяется выражением
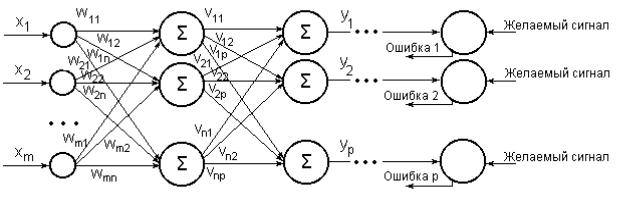
230
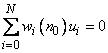 , (3.19)
, (3.19)
а персептрон корректно классифицирует как сигналы, которые принадлежат к обучающей выборке 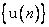 .
.
Из рис. 3.6.2 следует, что не существует прямой, которая отделила бы точки со значениями функции исключающего ИЛИ (XOR), равными 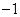 , от точек со значениями, равными 1. В этом случае роль примерной границы играет эллипс,
, от точек со значениями, равными 1. В этом случае роль примерной границы играет эллипс,
и поэтому алгоритм (2.18) не был бы сходящимся. Проблему XOR можно разрешить с помощью двухслойного персептрона.
Многослойная нейронная сеть
Рис. 3.6.3.. Многослойная нейронная сеть.
В каждом слое расположено 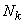 нейронов с нелинейной функцией (сигмоидой либо гиперболическим тангенсом). Нейронная сеть имеет m входов, на которые подаются входные сигналы x1(n),… xm(n).
нейронов с нелинейной функцией (сигмоидой либо гиперболическим тангенсом). Нейронная сеть имеет m входов, на которые подаются входные сигналы x1(n),… xm(n).
Выходной сигнал 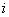 -го нейрона в p-м слое обозначается yi(n), i=1…p.
-го нейрона в p-м слое обозначается yi(n), i=1…p.
детальная структура 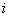 -го нейрона в p-м слое на рис 3.2.1.
-го нейрона в p-м слое на рис 3.2.1.
