
Нечеткая логика и нейронные cети
..pdf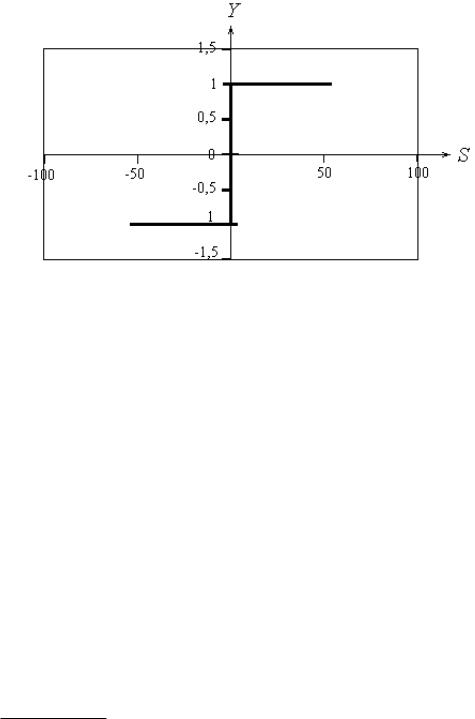
201
Р и с . 3.4.1.).. Бинарная пороговая функция
2. Сигнум, или модифицированная пороговая функция, для которой значение
S0=0 (рис. 3.4.2), задается уравнением
1, S S0
Y (s) 0, S 0
1, S S0
Р и с . 3 4 .2. Функция сигнум
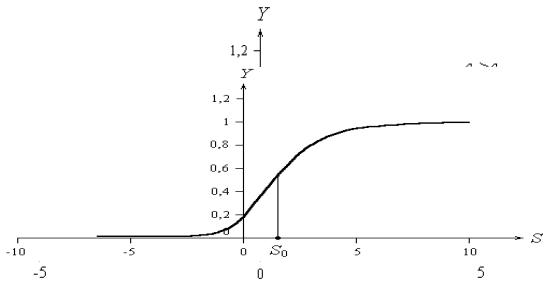
3. Сигмоидная логистическая функция (S-образная, имеющая две горизонтальные асимптоты и одну точку перегиба) является возрастающей сжимающей функцией, значения которой принадлежат интервалу (0; 1) (рис.
3 . 4 .3):
Y (s) |
|
1 |
1 exp(c s)
,
202
где с>0 – коэффициент, характеризующий крутизну логистической функции,
усиливающей слабые сигналы (S)).
Р и с . |
3 . 4 .4. Сигмовидная функция |
|
||
В общем случае сигмовидная функция определяется уравнением: |
||||
Y (s) |
1 |
,где S0 |
– значение смещения. Если значение |
|
|
|
|||
1 exp( c (s s0 )) |
||||
коэффициента с велико, то график общей сигмовидной функции приближается к пороговой функции (рис. 3 4 .4 ).
Р и с . 3 . 4 .4 . Общая сигмовидная функция
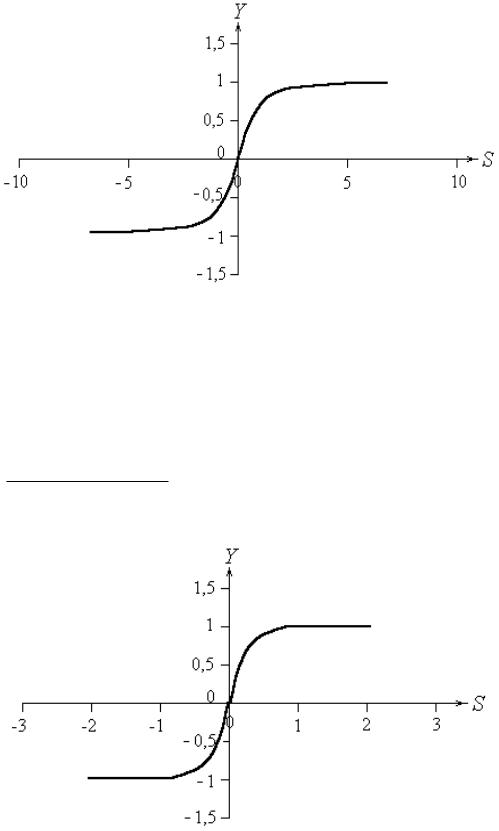
Биполярная сигмоидная функция (рис. 3 4 .5), уравнение которой
Y (s) |
2 |
1, |
|
||
1 exp( c s) |
203
принимает значения в диапазоне (-1; 1).
Ри с . 3 4 .5. Биполярная сигмовидная функция
4.Гиперболический тангенс (рис. 7) аналогичен биполярной логистической
функции без смещения и является симметричной функцией (tansig(S)):
Y (s) |
exp(c s) exp(c s) |
|
exp(c s) exp(c s) |
||
|
.
Р и с . 3 4 .6. Гиперболический тангенс
204
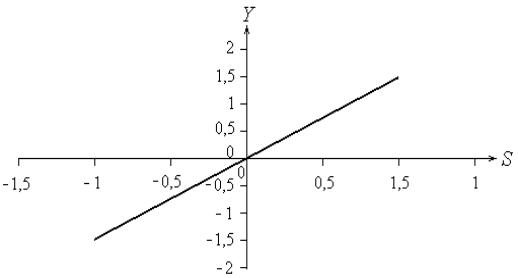
5. Линейная функция активации, уравнение которой Y(s)=k s, где k –
угловой коэффициент наклона прямой, представлена на рис. 3 3.7 (S).
Р и с . 3 4 .7. Линейная функция
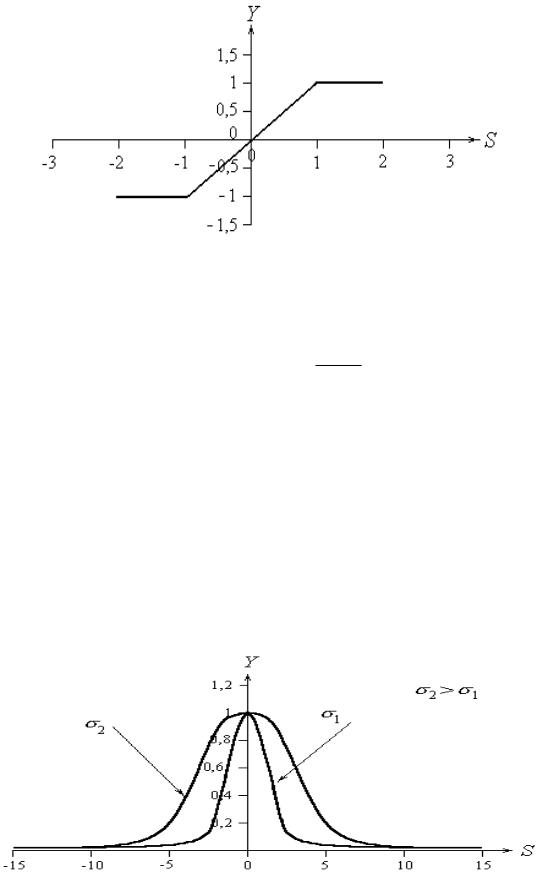
6. Линейная, ограниченная на отрезке [-a; a] функция активации (рис. 3 3.8)
определяется по формуле:
|
p, s a |
|
|
p, s a |
|
Y (s) |
||
|
s, a s a |
|
|
||
|
||
где p, как правило, равно единице: |
|
205
Ри с . 3 4 .8. Линейная ограниченная функция
7.Радиально-базисная функция активации характеризуется функцией Гаусса для нормального закона распределения, в соответствии с которой:
|
s |
2 |
|
|
Y (s) exp |
|
|
2 |
|
|
2 |
|
||
|
|
|
||
,
где – cреднеквадратичное отклонение, характеризующее крутизну радиально-
базисной функции (рис.10). Величина s определяется в соответствии с евклидовым расстоянием между входным и весовым векторами:
S2 =|X-W|2 =
|
n |
|
(xi |
i 1 |
|
w ) |
2 |
|
|
i |
|
.
Наряду с перечисленными функциями могут использоваться и другие функции активации, например, логарифмическая функция [2].
Р и с . 3 4 .9. Радиально-базисная функция Многомерные радиальные распределения позволяют производить многомерный
анализ путем сведения его к анализу одномерных симметричных распределений,
206
таких как многомерное нормальное распределение или равномерное в шаре с
центром в начале координат [6].
Выбор функции активации определяется:
1.Спецификой задачи.
2.Удобством реализации на ЭВМ в виде электрической схемы или другим способом.
3.Алгоритмом обучения: некоторые алгоритмы накладывают ограничения на вид функции активации, их нужно учитывать.
Чаще всего вид нелинейности не оказывает принципиального влияния на решение задачи. Однако удачный выбор может сократить время обучения в несколько раз.
3.5.Алгоритмы обучения нейронных сетей
Среди всех свойств искусственных нейронных сетей наиболее интересно так их способность к обучению, напоминающее процесс интеллектуального развития человека. Но возможности обучения искусственных нейронных сетей ограниченны, и нужно еще решить много сложных задач для понимания процедур обучения.
Сеть обучается, чтобы множества входов соответствовало желаемому множеству выходов. Каждое такое входное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал выходной вектор. Различают алгоритмы обучения с учителем и без учителя.
Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе
207
они называются обучающей парой. Обычно сеть обучается на некотором числе таких обучающих пар. Предъявляется выходной вектор, вычисляется выход сети и сравнивается с соответствующим целевым вектором, разность (ошибка) с
помощью обратной связи подается в сеть и веса изменяются в соответствии с алгоритмом, стремящимся минимизировать ошибку. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.
Несмотря на многочисленные прикладные достижения, обучение с учителем критиковалось за свою биологическую неправдоподобность. Трудно вообразить обучающий механизм в мозге, который бы сравнивал желаемые и действительные значения выходов, выполняя коррекцию с помощью обратной связи. Обучение без учителя является намного более правдоподобной моделью обучения в биологической системе. Развитая Кохоненом [3] и многими другими, она не нуждается в целевом векторе для выходов и, следовательно, не требует сравнения с предопределенными идеальными ответами. Обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны преобразовываться в некоторую понятную форму, обусловленную процессом обучения.
Большинство современных алгоритмов обучения выросло из концепций Хэбба
(см. 3.2.Нейрон Хебба). Им предложена модель обучения без учителя, в которой
208
синаптическая сила (вес) возрастает, если активированы оба нейрона, источник и приемник. Таким образом, часто используемые пути в сети усиливаются и феномен привычки и обучения через повторение получает объяснение.
В искусственной нейронной сети, использующей обучение по Хэббу,
наращивание весов определяется произведением уровней возбуждения передающего и принимающего нейронов. Это можно записать как
wij(n+1) = w(n) + α* xi*yi,
где wij(n) – значение веса от нейрона i к нейрону j до подстройки, wij(n+1) –
значение веса от нейрона i к нейрону j после подстройки, α – коэффициент скорости обучения, yi – выход нейрона i и вход нейрона j, xj – выход нейрона j.
Сети, использующие обучение по Хэббу, конструктивно развивались, однако за последние 20 лет были разработаны более эффективные алгоритмы обучения с учителем, приводящие к сетям с широким диапазоном характеристик обучающих входных образов и большими скоростями обучения, чем использующие простое обучение по Хэббу.
Адаптация и самоорганизация искусственных нейронных сетей достигается в процессе их обучения. Целью обучения нейронных сетей является такая подстройка их весов, которая обеспечивала бы для некоторого множества входов требуемое множество выходов.
При решении прикладных задач с помощью нейронных сетей необходимо собрать достаточный объем данных, для того чтобы обучить нейронную сеть решению этих задач. Обучающий набор данных – это набор наблюдений, содержащих признаки изучаемого объекта. Первоначальный выбор признаков осуществляется на основе имеющегося опыта, с учетом мнения экспертов. Вопрос о том, сколько необходимо иметь данных для обучения сети, оказывается непростым. Известны эвристические правила, устанавливающие связь между количеством
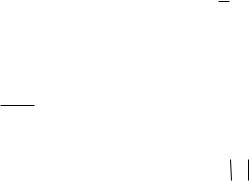
209
используемых для обучения данных и размерами сети. Простейшее из них гласит,
что количество наблюдений должно быть в 10 раз больше числа связей в сети.
Процесс обучения – это процесс определения параметров модели процесса или явления, реализуемого нейронной сетью. Ошибка обучения для конкретной конфигурации сети определяется после прохода через сеть всех имеющихся данных и сравнения выходных значений с целевыми значениями в случае обучения с учителем. Соответствующие разности позволяют сформировать так называемую функцию ошибок. Если ошибка сети, выходной слой которой имеет n
нейронов, ei yi ti есть разность между реальным и желаемым сигналами на выходе i-го нейрона, то в качестве функций ошибок могут быть использованы следующие функции:
|
n |
2 |
|
|
|
|
|
|
|
, |
|
|
|
||
сумма квадратов ошибок sse = ei |
|
|
|
||||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
|
средняя квадратичная ошибка |
mse = |
ei2 |
, |
||||
n |
|||||||
|
|
|
|
i 1 |
|
||
|
|
|
|
|
|
||
регулируемая или комбинированная ошибка
msereg =
n
n |
2 |
|
1 |
e |
|
||
|
|
|
|
i 1 |
i |
|
n |
|
|
n |
|
e |
|
|
2 |
i 1 |
i |
|
|
, где
- параметр регуляризации,
|
|
1 |
n |
|
средняя абсолютная ошибка mae = |
|
ei . |
|
|||
|
|
n i 1 |
|
При моделировании нейронных сетей с линейными функциями активации нейронов можно построить алгоритм, гарантирующий достижение абсолютного минимума ошибки обучения. Для нейронных сетей с нелинейными функциями активации в общем случае нельзя гарантировать достижение глобального минимума функции ошибки. Поверхность функции ошибок определяется как совокупность точек-значений ошибок в N+1-мерном пространстве всевозможных сочетаний весов и смещений с общим числом N. Цель обучения при
210
геометрическом анализе или изучении поверхности ошибок состоит в том, чтобы найти на ней глобальный минимум. В случае линейной модели сети и минимизации суммы квадратов ошибок поверхность ошибок представляет собой параболоид, имеющий единственную точку минимума. В случае нелинейной модели поверхность ошибок имеет сложное строение и может иметь локальные минимумы, плоские участки, седловые точки и длинные узкие овраги.
Как правило, при обучении такой сети вычисляется градиент функции ошибок в случайно выбранной точке поверхности, а затем эта информация используется для продвижения вниз по склону. Алгоритм продвижения завершается в точке минимума, локального или глобального. По существу алгоритмы обучения нейронных сетей аналогичны алгоритмам поиска глобального экстремума функции многих переменных.
Сети с большим количеством весов позволяют воспроизводить сложные функции, но в этом случае возможно так называемое «переобучение» сети, когда ошибки обучения малы, но полученная модель имеет слабое отношение к истинной зависимости. Нейронная сеть же с небольшим количеством весов может оказаться недостаточно гибкой, чтобы смоделировать имеющуюся зависимость. Для преодоления эффекта переобучения используется контрольная проверка. Часть обучающих наблюдений резервируется как контрольные наблюдения и не используется при обучении сети. Если контрольная ошибка перестает убывать или начинает расти, то это означает, что сеть слишком близко следует исходным данным и обучение следует остановить. В этом случае необходимо уменьшить количество нейронов или слоев, так как сеть является слишком мощной для решаемой задачи. Если же сеть имеет недостаточную мощность для воспроизведения имеющейся зависимости, необходимо добавить нейронов или даже слоев.
Способность сети, обученной на некотором множестве данных выдавать правильные результаты для достаточно широкого класса новых данных, в том
