Нечеткая логика и нейронные cети
..pdf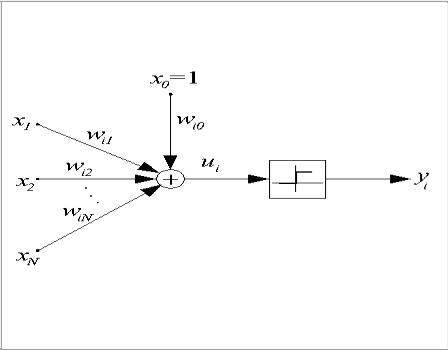
191
В простейших однослойных (без обратных связей и каскадов) сетях входные
сигналы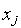 
нейрона — входные сигналы сети в целом, а выходные сигналы 
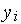нейрона — выходные сигналы сети в целом. В многослойных сетях роль
входных сигналов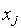 
некоторых нейронов играют выходные сигналы 
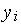предыдущих слоев ИНС.
Входному вектору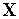 
значение 
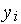определяет принадлежность входного вектора тому или иному 
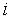-му классу. Cтепень успеха зависитот "правильности"
подбора/назначения весовых коэффициентов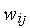 
и функции активации 
.
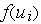Однако, в практических ИНС обычно функции активации назначаются однократно и подбираются только весовые коэффициенты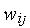 
.
Перцептрон предложен в 1943 г. и называется также моделью МакКаллока-
Пится. В этой модели искусственный нейрон считается бинарным элементом,
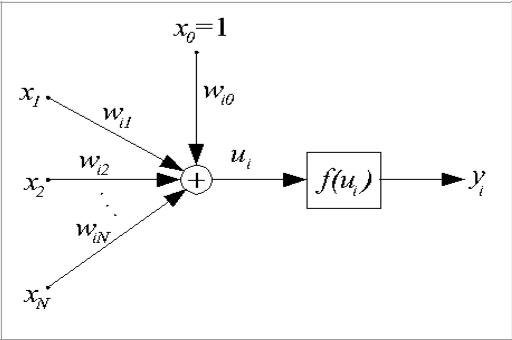
его структурная схема представлена на рис. 1.
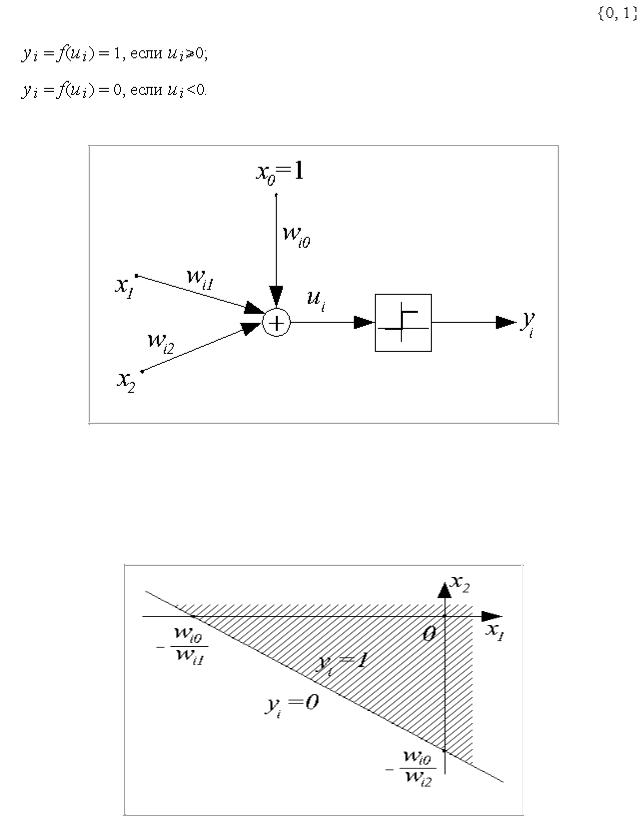
Рис. 3.3.2. Структурная схема персептрона
192
Выходной сигнал нейрона может принимать только два значения
Двухвходовой нейрон
Рис. 3.3.3. Структурная схема двухвходового персептрона Для нейрона выражение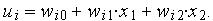 
определяет плоскость в
двухмерном пространстве, пересекающаяся с плоскостью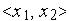 
по линии,
определяемой уравнением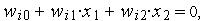 
(рис. 3.3.4)
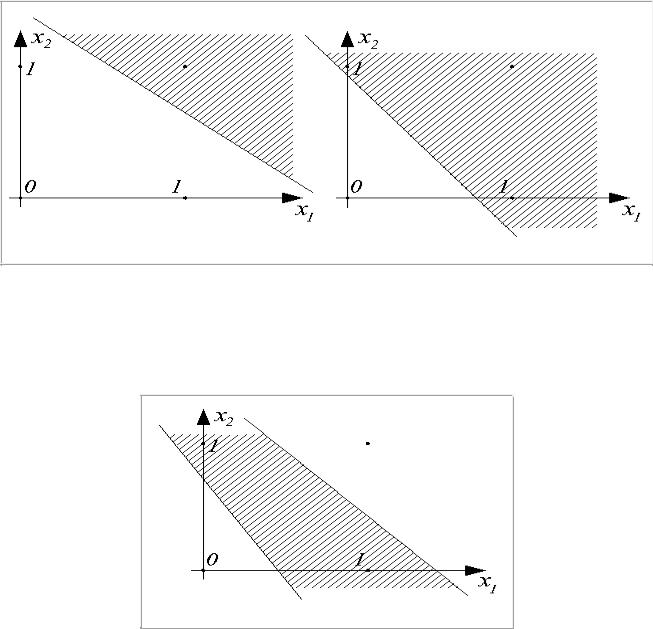
Рис.3.3.4 . Разделение пространства входных данных двухвходовым персептроном.
193
Пространство входных сигналов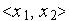 
делится на две области: в одной из них (штрих) значения 
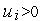, функция активации принимает значение 1; в
другой —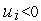 
, и 
.
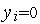Персептрон является простейшим линейным классификатором. С его помощью можно обеспечить, реализацию логических функций "И" и "ИЛИ" над входам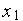и 
и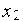 
, (рис. 4.)
Рис. 3.3.5. Реализация логических функций И и ИЛИ двухвходовым персептроном
Логическую функцию "исключающее ИЛИ" двухвходовым персептроном реализовать невозможно (Рис. 3.3.6).
Рис. 3.3.6. Разделение пространства входных данных для реализации функции
"исключающее ИЛИ"
194
Сигмоидальный нейрон
Сигмоидальный нейрон устраняет основной недостаток персептрона — разрывность функции активации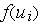 
. Структурная схема нейрона данного вида представлена на рис. 3.3.7 .
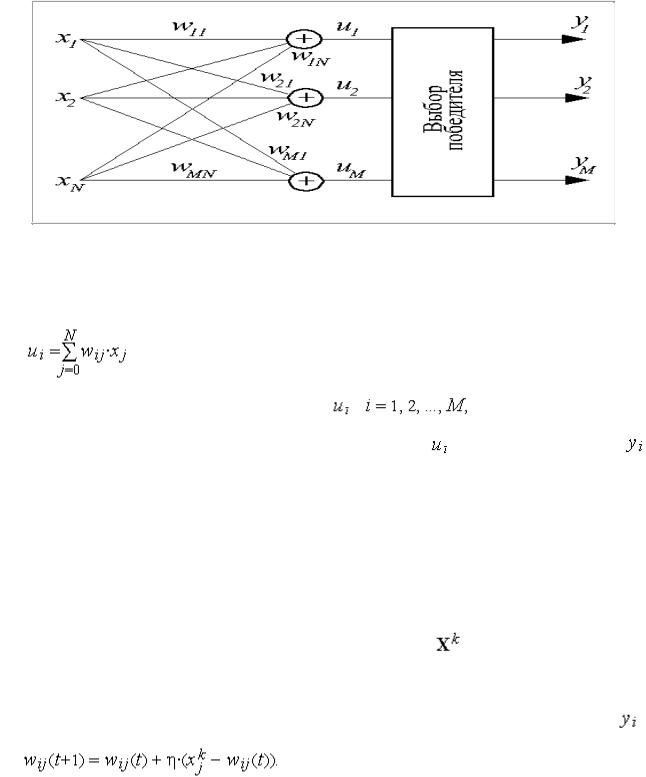
Рис. 3.3.7. Структурная схема сигмоидального нейрона В качестве функции активации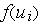 
выступает сигмоидальная функция. На
практике используются как униполярные, так и биполярные функции активации.
Нейроны типа WTA
Нейроны типа WTA (Winner Takes All — победитель получает все) всегда используются группами, в которых конкурируют между собой.
195
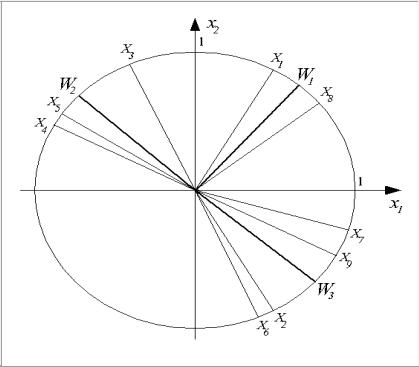
Рис. 3.3.8. Структурная схема слоя нейронов типа WTA
Каждый конкурирующий нейрон в группе получает одни и те же входные сигналы. Каждый нейрон рассчитывает выходной сигнал своего сумматора
. обычным образом |
|
|
|
По результатам сравнения всех |
, |
выбирается |
нейрон- |
победитель, обладающий наибольшим |
значением |
. Выходной |
сигнал |
нейрона-победителя получает значение 1, выходные сигналы всех остальных
нейронов — 0.
Для обучения нейронов типа WTA не требуется учитель. Начальные значения весовых коэффициентов всех нейронов выбираются случайным
образом с последующей нормализацией относительно 1. |
|
При предъявлении каждого обучающего вектора |
определяется нейрон- |
победитель, что дает ему право уточнить свои весовые коэффициенты по
упрощенному |
(в |
силу |
бинарности ) |
|
|
(3.2) |
|
Все проигравшие нейроны оставляют свои весовые коэффициенты неизменными.
196
В каждом цикле обучения побеждает нейрон, чей текущий вектор входных весов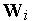 
наиболее близок входному вектору 
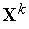. При этом вектор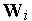 
корректируется в сторону вектора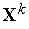 
. Поэтому в ходе обучения каждая группа близких друг другу входных векторов (кластер) обслуживается отдельным нейроном.
Результат обучения слоя нейронов типа WTA на последовательности девяти двухкомпонентных входных векторов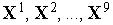 
иллюстрирует рис. 3.3.9.
Здесь были выделены три кластера входных векторов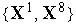 
, 
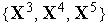
и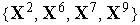 
. За их распознавание отвечают три нейрона с векторами входных весов 
, 
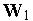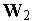и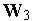 
соответственно.
Рис. 3.3.9. Результат обучения слоя нейронов типа WTA
При использовании нейронов типа WTA возникает возможность появления нейронов, ни разу не победивших в конкурентной борьбе в ходе обучения и поэтому оставшихся в начальном состоянии. Для исключения "ложных"
197
срабатываний в режиме классификации “мертвые” нейроны после окончания обучения должны быть удалены.
Для уменьшения количества “мертвых нейронов” (и, следовательно,
повышения точности распознавания) используется модифицированное обучение, основанное на учете числа побед нейронов и шрафовании наиболее
"зарвавшихся" среди них. Дисквалификация может быть реализована либо назначением порога числа побед, после которого слишком активный нейрон
"засыпает" на заданное число циклов обучения, либо искусственным уменьшением величины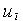 
пропорционально
Нейрон Хебба
Д. Хебб, в 1949 г. вычислил усиление связи двух взаимодействующих клеток при их одновременном возбуждении. Это позволило ему предложить правило
уточнения |
входных |
весов нейрона |
в |
следующем |
виде: |
|
|
|
|
|
(3.3) |
где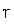 
— коэффициент обучения, значение которого выбирается из интервала (0,
1). Правило Хебба применимо для нейронов с различными функциями
активации. Обучение нейрона может производиться как с учителем, так и без
него. В первом случае |
в правиле Хебба вместо фактического |
|
значения выходного сигнала |
используется ожидаемая реакция |
. |
Особенностью правила Хебба является возможность достижения весом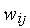 
произвольно большого значения за счет многократного суммирования приращения в циклах обучения. Одним из способов стабилизации процесса
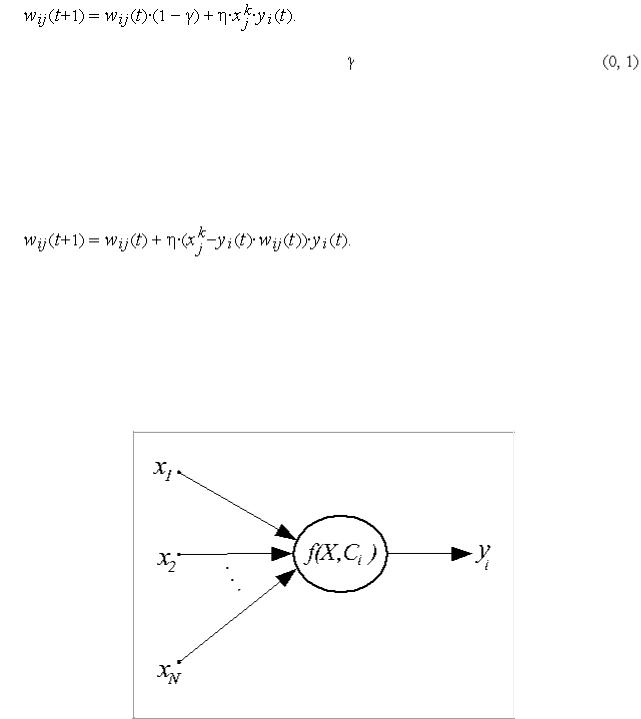
обучения по Хеббу служит уменьшение уточняемого веса |
на величину, |
пропорциональную коэффициенту забывания . При этом |
правило Хебба |
|
198 |
принимает |
вид |
(3.4) |
|
Значение коэффициента забывания выбирается из интервала |
, |
рекомендуется соблюдать условие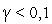 
.
При обучении по правилу Хебба нейрона с линейной функцией активации стабилизация не достигается даже при использовании забывания. В 1991 г.
Е.Ойя предложил модификацию правила Хебба, имеющую следующий вид:
Радиальный нейрон
Радиальные нейроны существенно отличаются от нейронов других типов.
Они используются только группами, составляя первый слой в многослойных радиальных нейронных сетях. Структурная схема такого нейрона дана на рис. 3.3.10.
Рис. 3.3.10 . Структурная схема радиального нейрона Здесь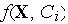 
— радиальная функция с центром в точке с координатами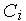 
. Такие функции разнообразны, но на практике чаще всего используется
функция Гаусса, имеющая следующий вид:
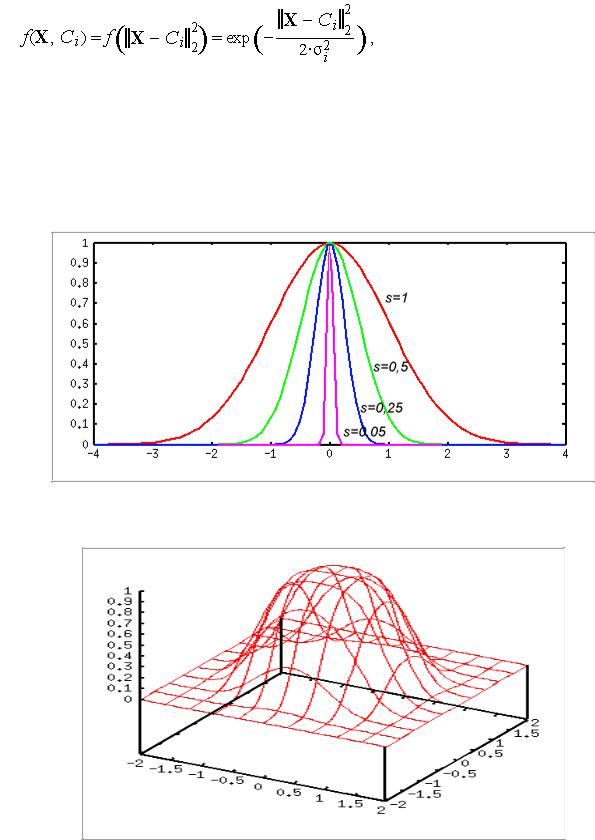
199
(3.5)
где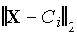 
— эвклидова норма расстояния между входным вектором 
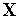и центром 
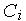нейрона, 
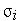— параметр, определяющий "ширину" функции. На рис. 3.3.10 представлены графики этой функции в скалярном варианте для различных значений 
.
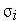Рис. 3.3.11 . График одномерной радиальной функции На рис. 3.3.12 дан график для двух входных сигналов.
Рис. 3.3.12. График двумерной радиальной функции
200
Принципиальное отличие радиального нейрона от сигмоидального нейрона и персептрона в том, что они разбивают многомерное пространство входных сигналов гиперплоскостью, а радиальный — гиперсферой.
Обучение радиального нейрона заключается в подборе параметров радиальной функци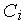и 
и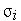 
.
3.4. Активационные функции нейронных элементов |
|
|||
Наиболее |
распространенными |
функциями |
активации, |
нелинейными |
усилительными характеристиками нейронного элемента или передаточными функциями являются следующие: пороговая, сигнум, логистическая,
гиперболический тангенс, линейная, линейная ограниченная, радиальная базисная и др.
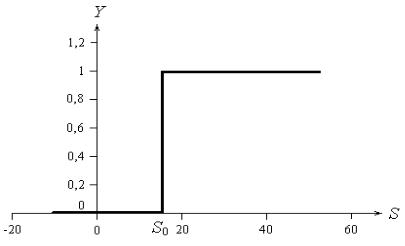
1. Пороговая бинарная функция – это функция, для которой нейронный элемент
остается |
неактивным до достижения входом порогового значения S0 (рис. |
|
3.4.1.). |
|
|
|
|
|
0, S S |
||
Y (s) |
|
0 |
|
|
|
1, S S |
0 |
|
|
|
|
Если S0=0 , то бинарная пороговая функция называется единичной функцией активации с жестким ограничением (hardlim(S)).