
Нечеткая логика и нейронные cети
..pdf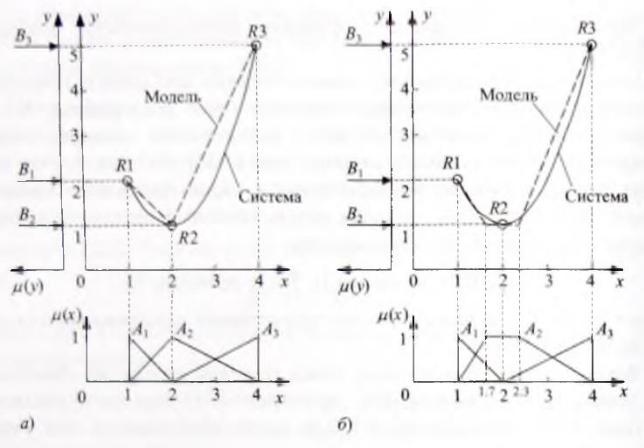
161 R1, R2, R3 — интерполяция имеет нелинейный характер, но при этом является локально линейной. Использование на участках между «существенными » точками модели Мамдани нелинейной интерполяции может привести к повышению точности модели, из-за того, что характер изгиба поверхности модели между данными точками будет совпадать с характером изгиба поверхности системы.
Рис. 2.6.2. Влияние изменения функции принадлежности нечеткого множества
А2 на вид характеристики модели
На практике характер выпуклости указанной поверхности в общем случае неизвестен, и имеется лишь небольшой объем информации о координатах отдельных точек, для которых выполнялись измерения. Кроме того, в случае нечеткой модели на характер выпуклости поверхности влияет столь большое
162
число элементов модели, что предугадать тип локальной выпуклости
оказывается достаточно сложным, особенно для систем со многими входами.
Влияние типа оператора (используемого для агрегации условий в модели системы с двумя входами) на вид поверхности нечеткой модели.
Обычно для одного и того же входного вектора для различных операторов выходные значения будут также различными, хотя и могут совпадать в отдельных точках, например, в тех, которые задаются условиями правил, т. е. в «существенных» точках модели. Процедуры интерполяции, выполняемые моделью для операторов PROD и MIN будет различными. Поверхность нечеткой модели, соответствующая оператору PROD, является более гладкой,
чем в случае оператора MIN. Чтобы определить, какая модель является более точной, необходимо иметь тестовое множество измерений векторов значений входных и выходных параметров моделируемой системы, на основе которого следует найти величину средней (либо квадратичной) ошибки.
Для каждого сегмента входного пространства Х1 и Х2 участки поверхности будут задаваться по-разному. Для оператора PROD, являющегося нелинейным,
интерполяционные поверхности являются линейными.
Используя непрерывно дифференцируемые функции принадлежности входных
параметров модели (например, гауссовы функции), можно обеспечить
непрерывность первой производной (а также производных более высоких
порядков) для данной поверхности, при условии, что не используются операторы типа MIN, связанные с возможностью резкого изменения значений.
Для любой нечеткой модели можно теоретически вывести формулу, задающую ее поверхность в явном виде (т. е. у = ƒ(X ) ) . Вместе с тем, на практике эти формулы не выводят в силу трудоемкости данного процесса, которая
значительно возрастает с увеличением числа входов |
и |
функций |
|
принадлежности. Значение на |
выходе нечеткой модели получают |
путем |
|
последовательного вычисления |
выходных значений отдельных |
ее элементов |
|
163
при заданном векторе входных значений X. С учетом этого, на практике, при применении модели Мамдани, точные формулы, задающие интерполяционную поверхность, неизвестны и приводит к получению различных нелинейных поверхностей со сложной формой определения.
Лингвистические и нелингвистические модели Мамдани
В самом начале практического использования в моделях Мамдани п
применялись |
только |
лингвистические |
переменные типа «малый» |
или |
«большой». |
Нечеткие |
модели, использующие подобные переменные |
для |
|
обозначения нечетких множеств, называются лингвистическим моделями. На практике, присвоение нечетким множествам лингвистических переменных часто оказывается лишенным особого смысла. Нечеткое множество «примерно
9» находится настолько близко к множеству «примерно 10», что считать его
«средним» можно лишь с большим трудом. Наличие большого числа множеств приводит к использованию большого числа переменных (например, «малый»,
«близкий к малому», «между малым и средним», «близкий к среднему»,
«средний» и т. д.), делает их трудноразличимыми. Лучше использовать термы в виде нечетких чисел («примерно 1», «примерно 2», «примерно 3» и т. п.),
поскольку с их помощью проще представить позицию каждого множества.
При малом числе нечетких множеств их ядра находятся на достаточно большом
расстоянии друг от друга. Нечеткие модели, в которых метки множеств
представлены в форме нечетких чисел, называются нелингвистическими моделями.
Для нечетких моделей правила «сообщают правду», если:
• для реализации операции И используются t-нормы, а для операции ИЛИ - s-
нормы, т. е. такие операторы, для которых выполняются условия µA∩0(x ) = 0 и µB∩1(y)≤ 1 (этим условиям не удовлетворяют, например, операторы SUM (арифметическая сумма) и MEAN),
164
• в качестве функций принадлежности входных нечетких множеств используются функции, имеющие конечный носитель (данному условию не удовлетворяют гауссовы функции) и принимающие нулевое значение в точках,
соответствующих модальным значениям (μ(х) = 1) смежных с ними функций.
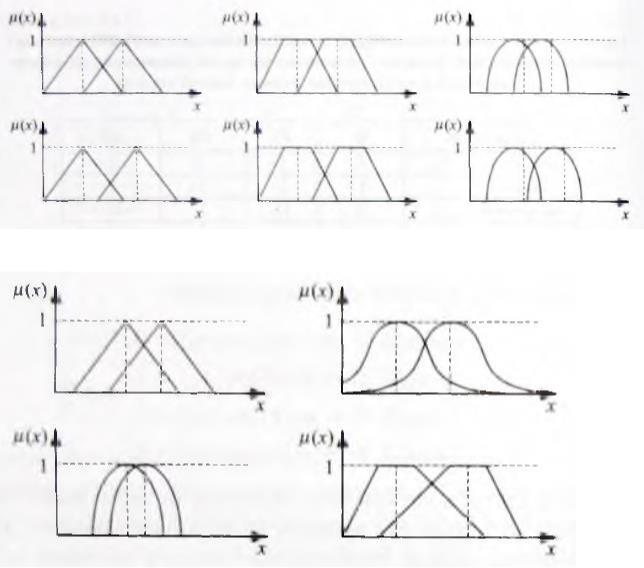
На рис.2.6.3. приведены примеры функций, позволяющие достичь эффекта
«сообщения правды» правилами, а на рис. 2.6.4, которые не позволяют
Рис. 2.6.3. Функции, позволяющие достичь эффекта «сообщения правды»
Рис. 2.6.4. Функции, не позволяющие достичь эффекта «сообщения правды»
165
Влияние удаленных (не являющихся смежными) опорных точек модели Мамдани на локальную интерполяцию. Существуют два способа построения
нечеткой модели.
1.На форму интерполяционной поверхности, соответствующей заданному сегменту входного пространства, влияют только те опорные точки, которые непосредственно примыкают к данному сегменту.
2.Влияние могут оказывать и некоторые другие (а иногда даже все), а не только непосредственно примыкающие точки. Настройка параметров функций принадлежности (адаптация модели на основе измерений данных о реальной системе) становится значительно сложнее.
Локальные интерполяционные поверхности, расположенные между каждой парой смежных опорных точек, зависят не только от этих, но и от всех остальных опорных точек, поскольку в каждой из интерполяционных формул присутствуют все координаты y, задаваемые заключениями правил
Анализ результатов использования функций принадлежности, носители которых выходят за пределы, задаваемые модальными значениями смежных функций принадлежности, позволяет сделать следующие выводы.
• Интерполяционная поверхность модели имеет тот же качественный тип (в
рассматриваемом примере линейный), что и в случае функций принадлежности, не выходящих за пределы модальных значений смежных с
ними функций. Таким |
образом, расширение носителей |
функций |
||
принадлежности не изменяет свойств интерполяции. |
|
|
||
• Настройка параметров |
модели должна |
происходить не |
локально, |
с |
использованием только непосредственно |
прилегающих опорных точек, |
а |
||
глобально, с использованием всех опорных точек системы. Учитывая явление,
называемое «проклятием размерности», глобальная настройка значительно сложнее локальной.
166
• Полученная после завершения процесса настройки модель является корректной (поверхность модели проходит через опорные точки Ri системы),
но при этом ее правила «не сообщают правду», что делает модель более сложной для понимания.
Таким образом, использование в моделях Мамдани функций принадлежности,
носители которых не выходят за пределы, задаваемые смежными с ними функциями (в частности, функций, удовлетворяющих условию разбиения единицы), является более предпочтительным.
2.7. Нечеткая модель Такаги—Сугено
Впервые модели Такаги—Сугено (TS-модели) были описаны в (Takagi 1985).
Эти модели также называют моделями Такаги—Сугено—Канга |
(Nquyen 1995; |
Yager 1994,1995), квазилинейными моделями и нечеткими |
линейными |
моделями (Babuska 1995а,b). От моделей Мамдани модели Такаги—Сугено отличаются формой правил. Если в случае модели Мамдани, описывающей систему с одним входом и одним выходом, правила имели вид ЕСЛИ (х есть А) ТО (у есть В)
(где А, В — нечеткие множества типа «малый» или «близкий к 5»), то в случае
TS-модели правила имеют вид ЕСЛИ (х есть А) ТО (у = f(x))
Вместо нечеткого множества заключение каждого правила содержит функцию f(x) , которая может быть нелинейной, хотя обычно используются линейные функции. Таким образом, правила TS-модели имеют вид
ЕСЛИ (х есть А) ТО (у = ах + b))
Если в модели база правил имеет вид
R1: ЕСЛИ (х есть А\) ТО (у = f ( x ))
……………………………………….
Rm : ЕСЛИ (х есть Аm) ТО (у = fm ( x )))
167
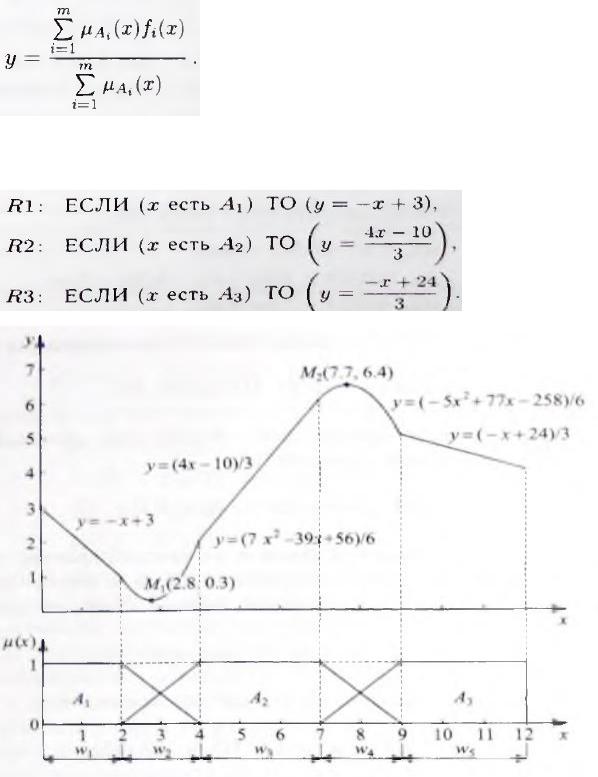
то значение на выходе модели вычисляется на основе степеней активизации отдельных заключений , fi, i = 1,..,m , в соответствии с формулой
Рассмотрим TS-модель с базой правил вида (5.120) и функциями
принадлежности, представленными на рис. 2.7.1:
(2.7)
Рис.2.7.1. Функции принадлежности входных параметров и поверхность отображения для рассматриваемой модели Такаги—Сугено

168
С помощью формул (2.7) введем следующие логические переменные:
Тогда функции принадлежности будут иметь вид
Рассматриваемые функции принадлежности удовлетворяют условию разбиения единицы:
Значение на выходе модели определяется по формуле:
(2.8.)
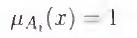
169
Анализ формулы (2.8) позволяет сделать вывод, что поверхность модели в точности соответствует заключениям правил только в тех областях входного пространства, степени принадлежности элементов которых соответствующим множествам Ai, удовлетворяют условию
(области w1, W3, w5). В областях, где эти степени являются дробными,
поверхность модели переходит из одной линейной формы |
(задаваемой |
соответствующим заключением) в другую. Ширина областей |
перехода |
определяется шириной областей дробных значений функций принадлежности
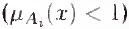 , а математическое выражение функций перехода зависит от типа используемых функций принадлежности.
, а математическое выражение функций перехода зависит от типа используемых функций принадлежности.
Функции перехода имеют квадратичную форму. Характеризующая модель 4)
функция непрерывна и не имеет скачков на границах областей. Вместе с тем,
производная этой функции непрерывной не является и изменяется на границах областей скачкообразно, что является следствием типа используемых функций принадлежности (их кусочной линейности). Непрерывность производной поверхности модели и, тем самым, большую гладкость последней можно обеспечить путем использования непрерывно дифференцируемых функций принадлежности, например гауссовых функций.
В данном примере использованы трапециевидные функции принадлежности,
имеющие зоны четкости, характеризующиеся тем, что их элементы полностью
(со степенью, равной 1) принадлежат соответствующему множеству. в
Поверхность модели с той же базой правил, но при условии использования других типов функций принадлежности будет отличаться.
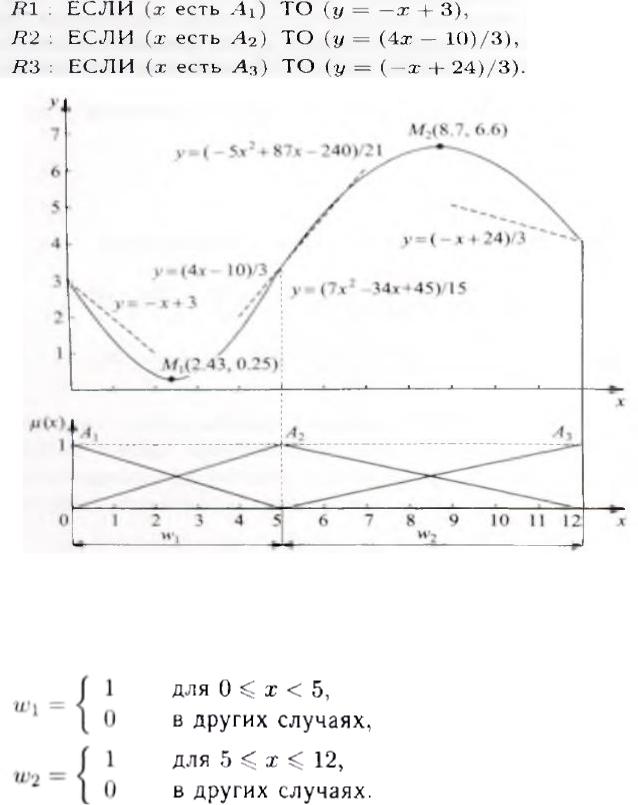
Рассмотрим TS-модель системы типа SISO с базой правил вида и треугольными функциями принадлежности, представленными на рис. 2.7.2:
170
ис |
|
Рис.2.7.2. Пример модели Такаги—Сугено с треугольными |
(не |
трапециевидными) функциями принадлежности |
|
Определим логические переменные w1, w2: |
|
Получим выражение, задающее поверхность модели:
