
Нечеткая логика и нейронные cети
..pdf101
Глава 2. Нечеткий вывод и нечеткие модели
2.1. Структура, основные элементы и операции в нечетких моделях
Классическая логика, оперирует только понятиями «истина» или «ложь», и не решает проблему неопределенности при выводах в человеческих суждениях.
Выражать неопределенность позволяет логическая система, в которой, кроме понятий «истина» или «ложь», используются другие значения истинности.
Такую систему предложил польский математик Ян Лукасевич с тремя значениями истинности: «0-ложь», «1-истина», «0,5-возможно». Затем появилась нечеткая логика с интервалом значений от 0 до 1.
Мышление человека основан на нечеткой логике и вместо чисел используется классы объектов в виде нечетких множеств с нечеткой истинностью, нечеткими связями и нечеткими правилами вывода. Нечеткая логика имеют следующие отличительные черты:
•использование лингвистических переменных вместо числовых переменных или в дополнение к ним;
•простые отношения между переменными описываются с помощью нечетких высказываний;
•сложные отношения между переменными описываются нечеткими алгоритмами.
Применение нечетких моделей целесообразно в случаях, когда имеются
недостаточность и неопределенность знаний об исследуемой системе,
Например, если:
•получение информации сложно или невозможно,
•источником основной информации являются экспертные данные,
эвристические описания процессов функционирования,
•информация о системе разнокачественная или оценка параметров проводится с использованием разных шкал.
102
Нечеткая логика использует обобщение направлений классической логики и
нечетких множеств, поэтому в интеллектуальных системах применяются различные модели нечеткого логического вывода.
Существуют нечеткие модели логического вывода:
- модель нечеткого логического вывода, представленная в виде сопоставления четкого набора нечетких ситуаций (описываемых кортежами нечетких
переменных) и соответствующих принимаемых решений. |
|
- модель нечеткого логического вывода построенная |
на нечетких |
отношениях при прямом произведении множества правил нечеткого логического вывода и нечеткого множества принимаемых решений.
- модель, представленную экспертным путем в виде нечетких эталонных ситуаций, связанных с определенными решениями (ситуационное управление).
- модель, основанная на нечетких (приближенных) высказываниях (суждениях),
нечетком выводе и построении логико-лингвистических моделей на основе композиционного правила Заде.
Под приближенными рассуждениями понимается процедура, при которой из некоторых посылок получают некоторые следствия, возможно также нечеткие.
Приближенные рассуждения лежат в основе способностей человека понимать естественный язык, играть в шахматы, разбирать почерк, требующие умственных усилий в неполностью определенной среде.
В классической двухзначной логике приближенные рассуждения основаны на следующих тавтологиях.
модус поненс: 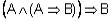 ;
;
модус толленс: 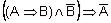 ;
;
силлогизм: 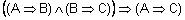 ;
;
контрапозиция: 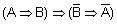 .
.

103
Основные правила вывода в двоичной логике
В четкой (двоичной) логике решения об истинности одних суждений выводятся на основании истинности других суждений. Такой вывод представляется в виде схемы: над горизонтальной чертой записываются все суждения, на основании которых принимается решение, а под чертой -
полученный результат. Схема корректного вывода обладает тем свойством, что поскольку истинны все суждения над чертой, то истинно также и суждение под чертой, так как из истинных суждений может выводиться только истинный результат.
Пусть |
и |
- это суждения (а не нечеткие множества), причем запись |
||
( |
) означает, что логическим |
значением суждения ( ) считается |
||
«истина», |
тогда как запись |
( |
) означает, что логическим значением |
|
суждения |
( ) считается «ложь». Два правила вывода часто применяются и в |
|||
двоичной логике. |
|
|
||
Правило вывода modus ponens
Условие |
|
А есть истинно |
Импликация |
|
Если А, то В – истинно |
|
|
|
Вывод |
|
В есть истинно |
|
|
|
|
|
|
Пусть суждение 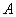 имеет вид «Ян является водителем», а суждение
имеет вид «Ян является водителем», а суждение 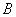 - «У Яна есть водительское удостоверение». В соответствии с правилом modus ponens,
- «У Яна есть водительское удостоверение». В соответствии с правилом modus ponens,
если 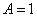 ,то и
,то и 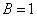 , поскольку если истинно, что «Ян является водителем», то также истинно, что «У Яна есть водительское удостоверение». Из истинности предпосылки и импликации (суждения над чертой) следует истинность вывода
, поскольку если истинно, что «Ян является водителем», то также истинно, что «У Яна есть водительское удостоверение». Из истинности предпосылки и импликации (суждения над чертой) следует истинность вывода
(суждения под чертой).
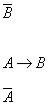
104
Правило вывода modus tollens
Условие |
|
|
Импликация |
|
(3.188) |
|
|
|
|
|
|
Вывод |
|
|
|
|
|
Понимается, что если «У Яна нет водительского удостоверения», т.е. 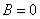 (
(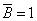
), то «Ян не является водителем», т.е. 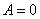 (
(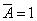 ). В этом примере тоже из истинности предпосылки и импликации следует истинность вывода.
). В этом примере тоже из истинности предпосылки и импликации следует истинность вывода.
Вместе с тем имеется ограничение: если высказывание А* близкое к А
(непрерывные значения в интервале 0 -1) является истинным, и если прецедент отсутствует, то модус поненс не сможет вывести никакого, приближенного заключения. Даже, при близком к A утверждении, что A' является истинным,
модус поненс не может быть применен. Поэтому возможным способом вывода при неопределенной информации является применение нечеткого логического вывода. Нечетким логическим выводом называется получение заключения в виде нечеткого множества, соответствующего текущим значениях входов, с
использованием нечеткой базы знаний и нечетких операций. Поэтому в нечеткой логике применяется композиционное правило Заде. (см 1.7. Суждения,
присутствующие в правилах modus ponens и modus tollens, представляются нечеткими множествами.
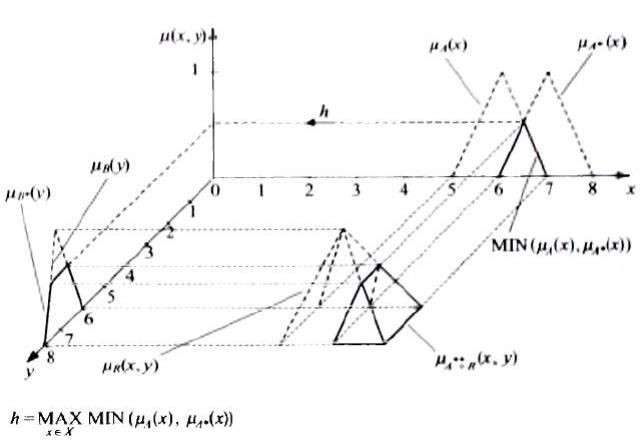
Пусть А и B два универсальных множества с базовыми переменными x и y
соответственно, R — нечеткое отношение двух аргументов, заданное на области определения X и Y. Результатом композиции А* и R (обозначается A*o
105
R) является нечеткое множество В* с областью определения Y и функцией принадлежности, имеющей вид:
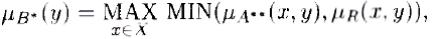 2.1.
2.1.
где R(х, у) —продолжение множества А*(х) на область определения X х У.
Операция MIN - t – норма, а операция MAX – Это S – норма. (Рис 2.1.1. )
В результате композиции отношения R(x, y) и нечеткого множества .А*,
получается нечеткое множество А*о R(x, y), функция принадлежности которого имеет вид поверхности в трехмерном пространстве.
Рис. 2.1.1. Нечеткий вывод на основе правила ЕСЛИ (х = А) ТО (у = В) в случае,
когда входным параметром х модели является нечеткое множество А*(х)
Проекция композиции А* о R на область определения Y приводит к получению модифицированного нечеткого множества В*, соответствующего заключению

106
используемого правила. Функция принадлежности этого множества имеет вид
(2.1) и представляет собой функцию µв(у), высота которой ограничена значением h, выражающим степень выполнения условия принадлежности множеству.
Пусть X и Y = {1,2,3,4}
Нечеткое множество A = “малый” задается таблицей
Элемент |
1 |
|
2 |
|
|
3 |
4 |
|
|
|
|
||
множества А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μA (x) |
1 |
|
0.6 |
|
|
0.2 |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
Нечеткое множество R = “примерно равны” представлено матрицей |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x |
y |
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
0.5 |
0.5 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
0.5 |
|
0.5 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
0 |
0.5 |
1 |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
0 |
|
0.5 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда, cсогласно композиционному правилу, B=Aº R |
|||||||||||||
|
|
0.5 |
0 |
|
0 |
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|||||
|
|
0.5 |
1 |
|
0.5 |
0 |
|
|
|
|
|
||
[1 0.6 0.2 0] º |
|
0 |
0.5 |
1 |
|
0.5 |
= [ |
1 0.6 |
0.5 0.2 ] |
||||
|
|
0 |
0 |
0.5 |
1 |
|
|
|
|
|
|||
То есть B представляет нечеткое множество |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Элемент |
1 |
|
2 |
|
|
3 |
4 |
|
|
|
|
||
множества B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μB (y) |
1 |
|
0.6 |
|
|
0.5 |
0.2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
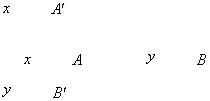
107
Результат объясняется следующим образом:
B = “более и или менее малый”, если терм “более или менее” представляется,
как оператор увеличения нечеткости
x |
- малый |
условие |
|
x, y |
- примерно равны условие |
||
|
|
|
|
y – более или менее малый |
нечеткий вывод |
||
Обобщенное (нечеткое) правило вывода modus ponens
Условие |
это |
Импликация |
IF это THEN это |
|
|
Вывод |
это |
|
|
где 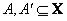 и
и 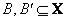 - нечеткие множества, а
- нечеткие множества, а 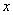 и
и 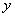 - лингвистические переменные типа «малая скорость», «умеренная температура» или «молодой человек». Формализуются такие переменные приписыванием им некоторых нечетких множеств. Схема вывода с лингвистическими переменными:
- лингвистические переменные типа «малая скорость», «умеренная температура» или «молодой человек». Формализуются такие переменные приписыванием им некоторых нечетких множеств. Схема вывода с лингвистическими переменными:
Условие |
Скорость автомобиля большая |
|
|
||
Импликация |
Если скорость автомобиля очень |
|
|
||
|
большая, то уровень шума высокий |
|
|
|
|
Вывод |
Уровень шума в автомобиле не очень |
|
высокий |
||
|
||
|
|
В этой схеме условие, импликация и вывод - неточные утверждения. В качестве лингвистических переменных выделим: 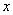 - скорость автомобиля,
- скорость автомобиля, 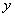 - уровень шума.
- уровень шума.

108
Терм 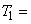 {«малая», «средняя», «большая», «очень большая»}
{«малая», «средняя», «большая», «очень большая»}
- множество значений лингвистической переменной 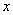 .
.
Терм 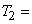 {«малый», «средний», «не очень высокий», «высокий»}
{«малый», «средний», «не очень высокий», «высокий»}
- множество значений лингвистической переменной 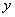 .
.
Каждому терму 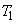 и
и 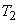 соответствует нечеткое множество. Из анализа этих схем вывода получаем нечеткие множества:
соответствует нечеткое множество. Из анализа этих схем вывода получаем нечеткие множества:
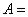 «очень большая скорость автомобиля»,
«очень большая скорость автомобиля»,
«большая скорость автомобиля» и |
«высокий уровень шума», |
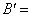 «не очень высокий уровень шума».
«не очень высокий уровень шума».
Различия между четким и нечетким правилами следующие (см также раздел
1.7). В обоих случаях импликация имеет один и тот же вид 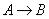 , где
, где 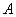 и
и 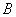 -
-
это суждения (правило) либо нечеткие множества. Суждение 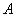 из импликации четкого правила также присутствует в предпосылке этого правила. В то же время условие нечеткого правила не связано с нечетким множеством
из импликации четкого правила также присутствует в предпосылке этого правила. В то же время условие нечеткого правила не связано с нечетким множеством 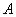 , но содержит некоторое нечеткое множество
, но содержит некоторое нечеткое множество 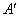 , которое может в определенном смысле быть близким к
, которое может в определенном смысле быть близким к 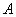 , однако не обязательно
, однако не обязательно 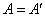 .
.
Нечеткое множество 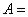 «очень большая скорость автомобиля» не равно нечеткому множеству
«очень большая скорость автомобиля» не равно нечеткому множеству 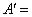 «большая скорость автомобиля» и выводы схем отличаются друг от друга. Вывод нечеткого правила относится к нечеткому множеству
«большая скорость автомобиля» и выводы схем отличаются друг от друга. Вывод нечеткого правила относится к нечеткому множеству 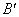 , определяемое композицией нечеткого множества
, определяемое композицией нечеткого множества 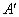 и нечеткой импликации
и нечеткой импликации 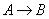 , т.е.
, т.е.
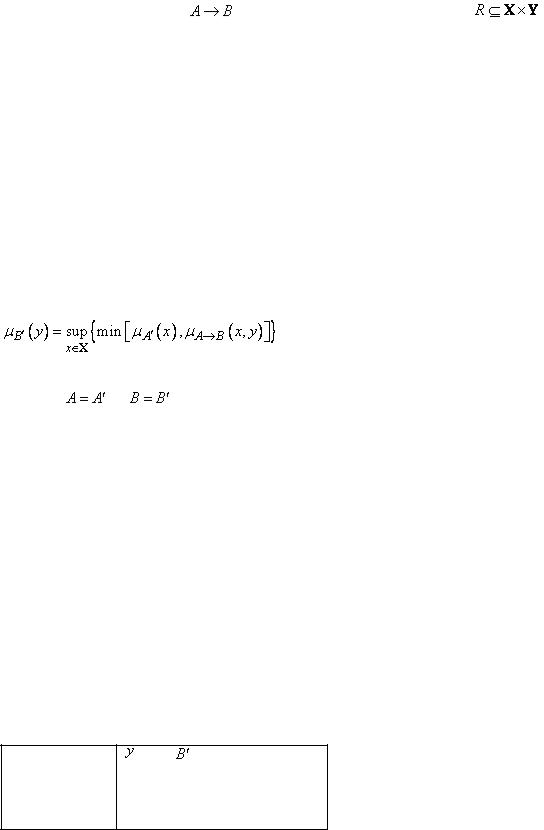
109
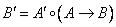 .
.
Нечеткая импликация |
есть нечеткое отношению |
с функцией |
принадлежности 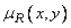 , а функцию принадлежности нечеткого множества
, а функцию принадлежности нечеткого множества 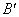 представиляют выражением
представиляют выражением
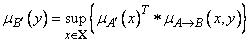 , где
, где
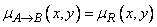 .- это функция принадлежности отношения
.- это функция принадлежности отношения 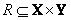
В частном случае, когда 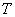 -норма имеет тип min
-норма имеет тип min
.
Если |
и |
, |
то обобщенное нечеткое правило modus ponens упрощается до правила классического modus ponens.
Обобщенное нечеткое правило modus tollens
Обобщенное (нечеткое) правило вывода modus tollens, где 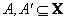 и
и 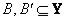 -
-
это нечеткие множества, в то время как 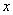 и
и 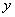 - это лингвистические переменные.
- это лингвистические переменные.
Условие |
это |
Импликация IF 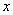 это
это 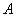 THEN
THEN 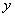

110
|
это |
|
|
Вывод |
это |
|
|
Подобный пример с лингвистическими переменными со скоростью автомобиля и уровнем шума:
Условие |
Уровень шума в автомобиле не очень |
|
|
|
высокий |
Импликация |
|
|
Если скорость автомобиля очень большая, |
|
то уровень шума высокий |
|
|
Вывод |
Скорость автомобиля большая |
|
|
Нечеткое множество 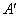 в выводе схемы (3.195) определяется комбинацией отношений
в выводе схемы (3.195) определяется комбинацией отношений
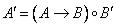 ,
,
Причем |
. |
Если 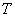 -норма имеет тип min, то
-норма имеет тип min, то 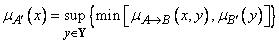 .
.
Если 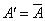 или
или 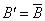 ,
,
то обобщенное нечеткое правило вывода modus tollens упрощается до классического правила modus tollens.
