Нечеткая логика и нейронные cети

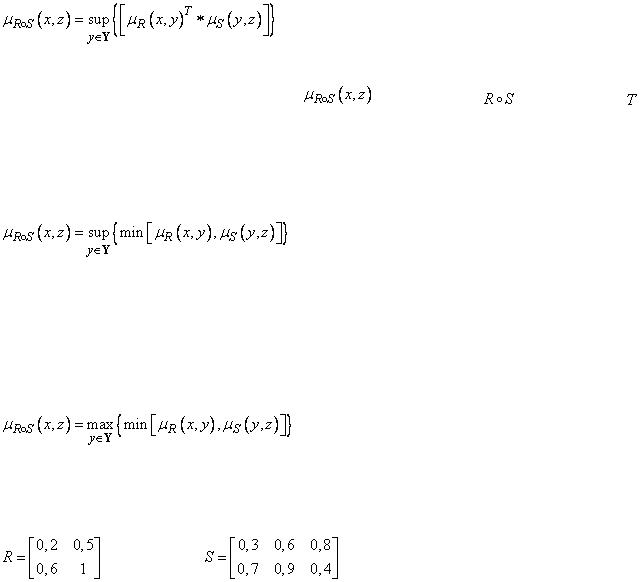
91

.

Для нечеткой логики важны комбинации двух нечетких отношений. Рассмотрим три четких множества , , 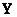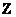и два нечетких отношения 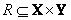и 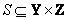c функциями принадлежност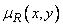и и .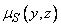

Комбинацией типа 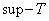нечетких отношени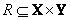й и 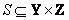называется нечеткое отношение 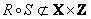с функцией принадлежности

нормы. Если в качестве 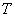-нормы применяется 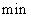, (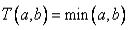), то равенство можно представить в виде

.

Это «комбинация типа sup-min».

Если множество 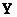имеет конечное количество элементов, то комбинация типа

sup-min сводится к комбинации типа max-min в форме

.

Если отношения 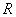и 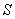представлены матрицами

,

где

,

,

,

,

,

.

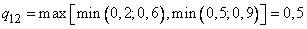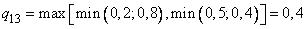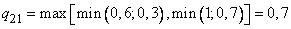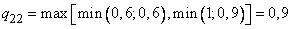Поэтому

.

Для практики нужны комбинации нечеткого множества с нечетким

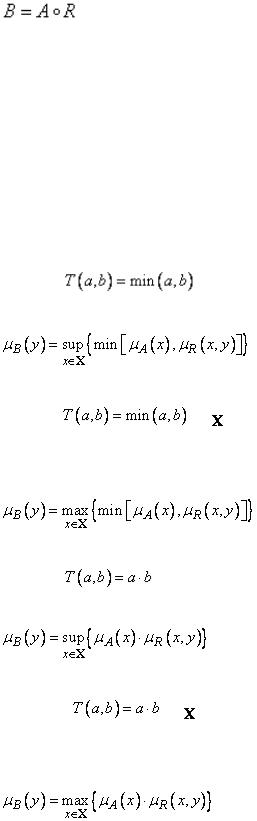
93

с функцией принадлежности

.

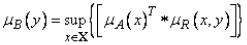Форма записи этого выражения зависит от используемой 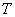-нормы и от свойств множества 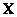. Возможны 4 случая:

комбинация типа mах-произведение (max-prod)

.

Для 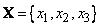, 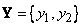и и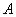меет вид

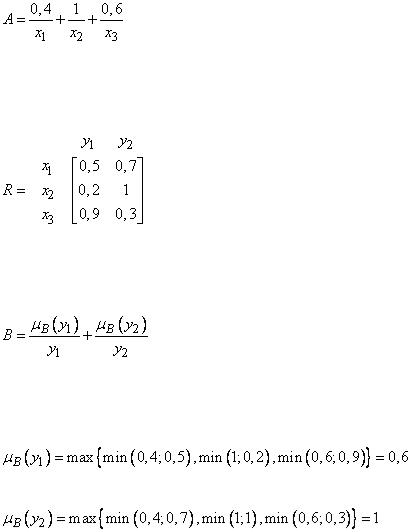
94

,

отношение 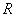представлено матрицей

.

Комбинацию 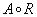получаем для max-min в виде нечеткого множество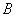

,

причем

,

.

Поэтому

.

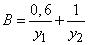1.7. Нечеткая импликация

Импликацией называется вид отношения, имеющего форму правила,

используемого при рассуждениях. Различают классическую и нечеткую импликации.

Классическая импликация выражается с помощью соотношения ЕСЛИ А ТО В

95

Сокращенная ее форма имеет вид:

А 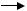B,

где A — утверждение, называемое антецедентом (условием), B - утверждение,

называемое консеквентом (заключением, результатом).

Утверждения в классической логике могут быть абсолютно истинными (А = 1,

В = 1) либо ложными (А= 0, В=0). Истинность или ложность импликации

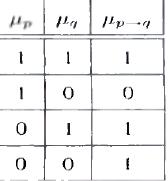
истинности и вычисляется по выражению

μA—B(x,y)=MAX (1 - μA, μB )

Функция принадлежности классической импликации μA—B

Оператор классической импликации имеет ряд свойств, затрудняющих его использование в нечеткой логике.

Импликация следующего вида:

ЕСЛИ (состояние автомобиля A = новый), ТО (расход топлива B = малый)

Область значений A переменной «состояние автомобиля» имеет бинарную форму представления (новый: х = 1, старый: х = 0). Аналогичным образом задана область значений B переменной «расход топлива» (малый: у = 1,

большой: у = 0).

96

Утверждение (состояние автомобиля = новый) = A является антецедентом,

Утверждение (расход топлива == малый) = B является консеквентом.

Заменяя лингвистические значения (новый, старый) на х и значения (малый,

большой) на у, получаем четыре возможных состояния Si импликации. S1: ЕСЛИ (состояние автомобиля = новый) ТО (расход топлива = малый), μA = 1, μB = 1, μA—B = 1

При х = новый, у = малый импликация является истинной.

S2: ЕСЛИ (состояние автомобиля = новый) ТО (расход топлива = большой), μA = 1, μB = 0, μA—B = 0

При х = новый и у = большой импликация является ложной.

Условие (состояние автомобиля = новый) не изменилось, и потому изменившееся заключение (расход топлива = большой) не может быть истинным.

S3: ЕСЛИ (состояние автомобиля = старый) ТО (расход топлива = малый), μA = 0, μB = 1, μA—B = 1

При х = старый и у = малый импликация является истинной. Эта импликация касается только факта (состояние автомобиля = новый), не говоря ничего о противоположном ему факте (состояние автомобиля = старый). Согласно классической логике в данном случае могут быть истинными как заключение

(расход топлива = малый), так и заключение (расход топлива = большой),

входящее в S4.

S4: ЕСЛИ (состояние автомобиля = старый), ТО (расход топлива = большой), μA = 1, μB = 1, μA—B = 1. Импликация для данных значений х, у является истинной также, как и в S3.

Недостаток оператора классической импликации состоит в том, что если условие вообще не выполняется (μB = 0), то импликация является истинной, и

это приводит к взаимно исключающим выводам (расход топлива = малый) и (расход топлива = большой).

97

В случае нечетких систем, при одновременной активации множества нечетких правил, использование оператора классической импликации оказывает неправильное представление. Поэтому нужны однозначные операции.

Нечеткая импликация представляет собой правило, простейшая форма которого выражается в виде ЕСЛИ (х = А) ТО (у = В),

где (х = А) — условие (антецедент), а (у = В) — заключение (консеквент).

Здесь А и В — нечеткие множества, заданные своими функциями принадлежности μA, μB и областями определения Х и Y соответственно.

Обозначение нечеткой импликации имеет вид:

А -> В.

Различие между классической и нечеткой импликацией состоит в том, что в случае классической импликации условие и заключение могут быть либо абсолютно истинными, либо абсолютно ложными, в то время как для нечеткой импликации допускается истинность, со значением, в непрерывном интервале

[0,1]. В практике редко встречаются ситуации, когда условия правил удовлетворяются полностью, и по этой причине нельзя полагать, что заключение абсолютно истинно. Нечеткая импликация (нечеткое отношение)

задается функцией принадлежности, область определения которой является декартовым произведением X х Y соответствующих областей условия и заключения.

Функция принадлежности импликации есть основа для нечетких выводов при вычислении выходного значения нечеткой модели (регулятора) с заданными входными значениями. Формирование нечеткого вывода, используя функции принадлежности условия μA(x) и заключения μB(y), осуществляют оператором импликации. Это может быть оператор импликации Мамдани, основанный на

99

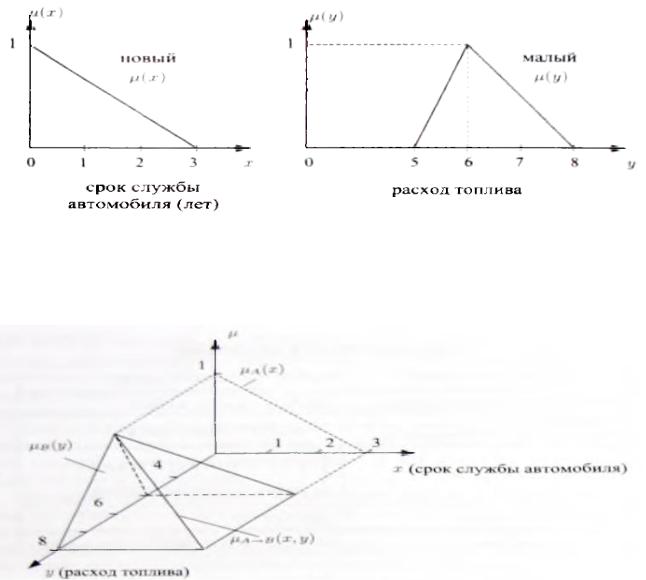
Функция принадлежности импликации μA—B(x,y) представлена на рис. 4.34.

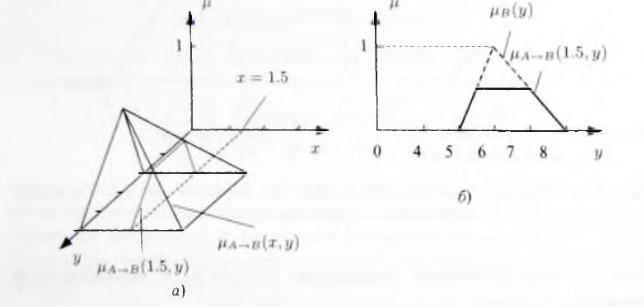
Используя подходящий метод вывода и имея определенное значение хо переменной х, содержащейся в условии правила, можно определить функцию принадлежности заключения μB(y), которую затем можно использовать для вычисления четкого значения у на выходе нечеткой модели (рис. 1.6.1).

Рис. 1.6.1. Функции принадлежности нечетких множеств «новый» и «малый»,

содержащихся в условии и заключении функции принадлежности импликации

μA—B(x,y) с использованием оператора Мамдани.

Рис. 1.6.2. Функция принадлежности импликации (оператора Мамдани )

100

Рис. 1.6.3. Функция принадлежности импликации μA—B(x,y) для заданного значения переменной х = = 1.5 (а) и ее проекция на плоскость {μ, y} (б)

.