Электромагнитные поля и волны

расстоянии r12 друг от друга, определяют с помощью закона Кулона:

где S-площадь заряженной поверхности.

3.2. Примеры расчета электростатических полей

Задача №1

Две плоские металлические пластины разделены слоем однородного

помощью уравнения Лапласа (3.5а) с применением граничных условий для потенциала на границе раздела диэлектрик-металл (3.9).

неизвестные постоянные подлежащие определению. Для их определения

На рисунке 3.2 изображены: распределение электрических зарядов на поверхностях электродов и электрическое поле между пластинами.

Задача №2

Сохраним условие задачи №1, но диэлектрическую проницаемость среды, заполняющей конденсатор, принимаем 0e y .

Решение:

Для данной задачи потенциал зависит от у, поэтому уравнение Лапласа

Неизвестные постоянные A и В могут быть определены из граничных условий:

Ёмкость конденсатора определяется с помощью известной формулы:

Задача №3

Сохраним формулу задачи №1, но добавим условие, что между пластинами в диэлектрике размещен заряд с объемной плотностью .

Решение:

В этом случае необходимо использовать уравнение Пуассона (3.5), из

64

Решение:

Пространство между пластинами разбиваем на две области: область Ι с диэлектриком, имеющую диэлектрическую проницаемость 1 и область ΙΙ,

имеющую диэлектрическую проницаемость 2 . Для каждой из областей

B 0 , A ( 2 / 1 ){U / d ( 2 / 1 1) b} , C U /{d ( 2 / 1 1) b}, D (U ( 2 / 1 1)d ) /{d ( 2 / 1 1) b} .

Потенциалы в областях имеют вид и удовлетворяют граничным условиям:

Для первой области:

1 ( 2 / 1 )Uy /{d( 2 / 1 1) b} при y 0 1 0 .

Для второй области:

2 U (d( 2 / 1 1) y) /{d( 2 / 1 1) b} при y d 2 U .

Напряженность электрического поля в первой и второй областях соответственно

Ey1 d 1 ( 2 / 1 )U /{d ( 2 / 1 1) b} ; dy

Ey 2 d 2 U /{d ( 2 / 1 1) b} . dy

граничных условий при y d . Емкость двухслойного конденсатора является последовательным соединением емкостей

C1 1S / d , C2 2 S /(b d ) , C C1C2 /(C1 C2 ) .

Задача №4

Определить потенциал , напряженность электрического поля E и

вектор электрического смещения D , двухслойного коаксиального конденсатора длиной L. Параметры диэлектриков и размеры конденсатора приведены на рис. 3.4. Заряд на поверхности внутреннего проводника конденсатора равен q , внешний проводник конденсатора заземлен.

Решение:

Для данной задачи, потенциал конденсатора описывается уравнением Лапласа в цилиндрической системы координат, в котором из соображений симметрии по координатам a и q, удерживается только одно слагаемое

Общее решение этого уравнения будет иметь вид Aln r B и для областей 1 и 2 запишется в виде:

1 A1 ln r B1 ; R1 r R2 (3.22)2 A2 ln r B2 ; R2 r R3 (3.23)

66

Для определения потенциала в данной, конкретной задаче необходимо определить неизвестные постоянные: A1,A2 ,B1,B2.

Для этого надо воспользоваться четырьмя граничными условиями для поля и потенциала.

Здесь -поверхностная плотность заряда на внутренней поверхности проводника конденсатора.

Используем первое граничное условие:

2 A2 ln R3 B2 0

откуда получим

A2 ln R3 B2

и, следовательно,

2 A2 ln Rr3 .

Из второго граничного условия

67

Из их сравнения следует, что потенциал непрерывен на границе раздела диэлектрик – диэлектрик при r R2 Далее запишем выражения для

Еr1, Еr 2 ,Dr1,Dr 2.

Решение:

Чтобы по заданному закону распределения потенциала в пространстве

68

(r,a, z) найти объёмный заряд, создающий это поле, необходимо

использовать уравнение Пуассона (3.5).

В нашем случае поле зависит только от r , поэтому в уравнении Пуассона записанного в цилиндрической системе координат оставляем слагаемое, зависящее только от координаты r .

путём последовательного дифференцирования, находим выражение для объемной плотности заряда

Примером применения уравнения Пуассона является хорошо известная в электронике задача о нахождении распределения объёмного заряда между катодом и анодом электроннолучевой трубки.

Задача №7.

Из плоского катода К вылетают электроны в направлении плоского анода А. Расстояние

между

электродами d много меньше их размеров. Катод заземлён, на анод подан потенциал U . Потенциал электрического поля между электродами

меняется по закону kx43 , здесь k –const (рис.

3.5).

Определить распределение объёмного заряда между электродами и поверхностный заряд на электродах.

Решение:

Для определения объемной плотности зарядов в области между электродами следует использовать уравнение Пуассона.

Потенциал зависит только от координаты х. (краевыми эффектами пренебрегаем). Поэтому получим

(x) 2 4 x 23 .x2 9

Плотность поверхностных зарядов на катоде и на аноде определяется . граничными условиями (3.9) В нашем случае нормалью к катоду будет ось х. Поэтому поверхностная плотность заряда на катоде будет

Аналогично нормаль к аноду противоположна по направлению оси x. Поэтому для анода

69

Попробуем разобраться, почему при x 0 объемная плотность заряда

х ?

Движение электронов от катода к аноду приводит к появлению тока

Задача №6.

Определить потенциал и напряженность электрического поля,

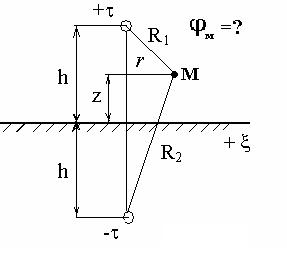
точечным зарядом q , расположенным над идеально проводящей плоскостью на высоте h (рис. 3.6).

70

Решение: Для решения следует использовать метод зеркального отображения и принцип суперпозиции. Метод зеркального отображения заключается в том, что металлическая поверхность заменяется зеркально отображенным зарядом –q . Используя этот метод и принцип суперпозиции,

записываем выражение для потенциала в точке М .

Задача №10

Определить напряженность электрического поля и потенциал в точке М , расположенной в свободном пространстве, создаваемые тонкой нитью,

Задача №11.

Над проводящей плоскостью, имеющей положительный поверхностный заряд , на высоте h , параллельно

ей подвешен заряженный провод с погонной плотностью заряда + (рис. 3.7). На какой высоте должен быть расположен провод, чтобы сила, действующая на него, равнялась нулю?

Решение:

При решении используем метод зеркального отображения без учета заряда на плоскости и принцип

суперпозиции потенциалов.

Для зарядов и - в точке М Рис. 3.7 потенциал не высоте h определяется из

соотношения