
Электромагнитные поля и волны
..pdf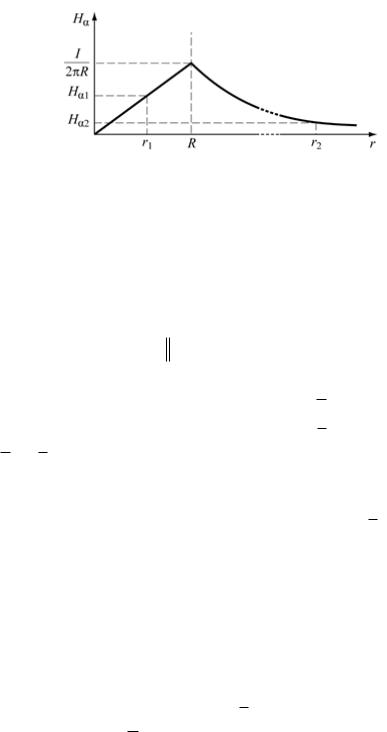
41
|
В области 1 охватываемый контуром ток меняется от 0 до I и равен |
|||
I |
Ir2 |
. Следовательно, |
|
|
|
|
|
||
1 |
R2 |
|
|
|
|
|
|
|
|
|
|
H 1 |
Ir |
|
|
|
|
. |
|
|
|
2 R2 |
||
График зависимости H r представлен на рис. 2.4.
Рис. 2.4. К задаче №6
Результат численного расчёта: H 1 0,16 А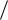 м , H 2 15,9 А
м , H 2 15,9 А м .
м .
Задача №7
Анизотропный диэлектрик имеет диэлектрическую проницаемость
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
0 |
. |
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|||
К нему приложено электрическое поле E x0 Ex z0 Ez . Найдите
выражение для вектора электрического смещения D . Определите угол между векторами E и D .
Решение:
Так как диэлектрик имеет анизотропную диэлектрическую проницаемость, то вектор электрического смещения D будет определен следующим выражением:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
Ex |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
D |
|
|
|
|
E |
0 |
0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ez |
|||||
Перемножая строку на столбец, получим проекции вектора смещения:
DX 1EX , DY EX , DZ 0 EZ .
Из них составим вектор смещения D
D x0 1Ex y0 Ex z0 0 Ez .
42
Для определения угла между векторами D и E запишем скалярное произведение векторов
D, E Dx Ex Dz Ez 
 Dx2 Dy2 Dz2
Dx2 Dy2 Dz2 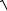
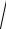 Ex2 Ez2 cos D, E ,
Ex2 Ez2 cos D, E ,
откуда
|
|
|
|
|
|
Dx Ex Dz Ez |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
D , E arccos |
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
D2 |
D2 |
D2 |
E2 |
E2 |
|
|
||
|
|
|
|
|
x |
y |
z |
|
x |
z |
|
|
|
Задача №8
Определить полный ток, если известно, что напряженность магнитного
поля H x0 5z sin t .
Решение:
Воспользовавшись первым уравнением Максвелла, находим:
|
|
|
|
x0 |
y0 |
|
z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rot H |
|
y0 |
5sin t jполн . |
||||||||
|
|
|
|
|
|
|
|||||
|
x |
y |
|
z |
|||||||
|
|
|
|
|
|
|
|
||||
|
|
|
5z sin t |
0 |
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Из полученного соотношения следует, что плотность полного тока jполн имеет только одну составляющую, направленную по оси y . Таким
образом:
jполн y0 5sin t.
Задача №9
Задано электрическое поле E E0 (x0 y y0 x) cos t . Определить
магнитное поле H .
Решение:
Используем 3-е уравнение Максвелла:
rot E Bt .
Найдем rot E :
|
|
|
|
x0 |
|
y0 |
z0 |
|
|
|
|
||
rot |
|
|
|
|
|
|
|
|
E |
cos t z |
2E cos t. |
||
E |
|||||||||||||
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
y |
z |
|
0 |
0 |
0 |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y |
x |
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|

43
Вектор В определим интегрированием полученного выражения для rot E по времени
|
|
z0 2E0 cos tdt , |
|
|
|
z0 |
2E0 |
sin t. |
||||||||||||||
B |
B |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя, материальное уравнение |
B |
H |
, находим выражение для |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вектора магнитного поля H : |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2E0 |
|
||||||||
|
|
|
|
|
|
|
B |
|
|
|
|
|
sin t. |
|||||||||
|
|
|
H |
H |
z |
|
|
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
0 |
||||||||||||||
Задача №10
В некотором объеме свободного пространства имеется электрическое
поле |
|
10 y В м и магнитное поле |
|
|
15x А м . Заряд |
q 10 9 K |
||||||||
E |
H |
|||||||||||||
0 |
|
|
|
|
|
|
|
|
0 |
|
||||
влетает в этот объем со скоростью |
106 z А м . Найти силу, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
действующую на заряд и её направление. |
|
|
|
|
|
|
||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
||||
На заряд, находящийся в магнитном и электрическом поле действует |
||||||||||||||
сила: |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
q |
|
|
|
|
|
|
|
|
||
|
|
F |
|
E B . |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сила электрического поля, воздействующая на заряд равна:
FЭ qE 10 9 10 y0 10 10 9 y0 .
Сила магнитного поля, воздействующая на заряд равна при В 0 Н (0 4 10 7 Гн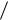 м ), определяется как векторное произведение скорости движения заряда и вектора магнитной индукции:
м ), определяется как векторное произведение скорости движения заряда и вектора магнитной индукции:
|
|
|
|
|
|
|
|
|
x0 |
y0 |
z0 |
|
|
|
|
|
|
|
|
|
|
|
106 |
|
18.84 10 9 y . |
||
F |
B |
|
0 |
0 |
|
||||||||
|
м |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
15 4 10 7 |
0 |
0 |
|
|
|
Суммарное воздействие сил электрического и магнитного полей |
|||||||||||||
направлено по оси y0 |
и равно по величине |
|
|
|
|
||||||||
|
|
|
|
|
|
|
F F F 28.84 10 9 |
H. |
|||||
|
|
|
|
|
|
|
|
э |
м |
|
|
|
|
Задача №11
Определить электродвижущую силу ( ЭДС ), возбуждаемую в квадратной рамке потоком вектора B H0 cos t . Направление вектора H относительно плоскости рамки показано на рис. 2.5.

|
44 |
n0 |
H |
45
a
a
a
Рис. 2.5. К задаче №11
Решение:
Поток вектора магнитной индукции определяется выражением
BdS ,
S
где S – площадь рамки.
Запишем значение для потока , проделав необходимые преобразования:
BdS Bn0dS cos 45 BdS cos 45 B dS
S S S S
|
1 |
|
H |
|
cos t a2 . |
|||||||
|
|
|
0 |
|||||||||
2 |
||||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
Величину электродвижущей силы ( ЭДС ) определяем следующим |
||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|||
ЭДС Ф |
|
1 |
|
H |
|
sin t a2 . |
||||||
|
|
|
|
0 |
||||||||
t |
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
Задача №12
|
|
|
Между полюсами электромагнита, создающего в |
зазоре индукцию |
|||
|
|
|
|
cos t , помещена круглая рамка, площадь которой |
S |
( S a2 |
, где |
B |
B |
||||||
0 |
1 |
1 |
|
||||
a – радиус рамки) много меньше площади полюсов электромагнита S и L – периметр рамки (рис. 2.6). Определить напряженность электрического поля, циркулирующую вдоль рамки и электродвижущую силу Э , наведённую в
контуре, если частота генератора |
f 400 Гц, амплитуда напряженности |
переменного магнитного поля B0 |
1 Тл , a 0,5 см ? Справка: Э Еl L . |
Как изменятся E и Э , если рамку повернуть на угол 60 относительно первоначального положения? Диэлектрик – воздух.

45
Рис. 2.6. К задаче №12
Решение:
Для решения этой задачи используется закон электромагнитной индукции (второе уравнение Максвелла в интегральной форме (2.2)).
По условиям задачи, поток вектора индукции, пронизывающий рамку, можно считать однородным и определяемым в виде
BdS Bn S1 cos .
S1
Здесь Bn – проекция вектора B на нормаль n к поверхности S1 . Согласно закону электромагнитной индукции, циркуляция вектора E по
замкнутому контуру равна |
скорости изменения этого потока / t , |
||||||||||||
пронизывающего площадку S1 . Запишем эти утверждения: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
В a2 cos t |
|
|
Э СEd l Еl L El 2 a |
|
0 |
|
B0 a2 sin t. |
|||||||||
|
t |
||||||||||||
|
|
L |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
При перпендикулярной ориентации рамки по отношению к |
|||||||||||
|
|
|
0 , наведённая |
|
|||||||||
вектору B , т.е. когда угол |
Э в контуре определяется |
||||||||||||
выражением |
Э a2 B sin t . |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Подставив заданные величины, получим |
|
|
|||||||||||
Э 1 (3,14) 0,5 10 2 2 400 sin 2 400t 0,0314 sin 2 400t В, |
|||||||||||||
откуда максимальная (амплитудная) величина Э равна |
|
||||||||||||
|
|
|
|
|
|
|
Э |
max |
3,14 10 2 |
В. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Напряженность электрического поля, циркулирующая вдоль рамки Еl равна отношению Э к периметру рамки L :
El Э / L Э / 2 a 1 (3,14) 0,5 10 2 2 400
sin 2 400t / (2 0,5 10 2 ) 0, 25 10 2 sin t В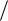 м.
м.

46
При повороте плоскости рамки на угол относительно магнитного
поля, E и Э уменьшаются в cos раз.
Ответ:
1) Максимальная Э , наводимая в контуре при перпендикулярной
|
|
|
|
||||||
ориентации рамки к вектору B0 , и |
напряженность электрического поля |
||||||||
соответственно равны Э |
max1 |
3,14 10 2 В и E |
|
0, 25 10 2 В м . |
|||||
|
|
|
|
|
max l |
|
|||
2) при повороте рамки на угол максимальная Э и напряженность |
|||||||||
электрического поля Э |
max 2 |
1,57 10 2 |
В, E |
1, 25 мВ м . |
|||||
|
|
|
|
|
max 2 |
|
|
||
Задача №13
Определить электродвижущую силу ( ЭДС ) в замкнутом контуре, образованном равнобедренным треугольником, если известен вектор H H0 sin t . Направление вектора H показано на рис. 2.7 и =600.
Рис. 2.7. К задаче №13
Решение:
Запишем выражение для потока вектора B H0 sin t :
0 sin t HdS ..
S
Скалярное произведение векторов HdS H0 cos S .
Учитывая (1.35), получим выражение для потока, пронизывающего треугольную площадку:
0 H0 sin t a2 . 2 2
Электродвижущая сила определяется соотношением
Э |
Ф |
|
|
a2 |
|
cos t. |
t |
0 |
H |
0 |
|||
|
|
|
4 |
|
||
|
|
|
|
|

47
. Задача №14
Две полубесконечные магнитные среды, 1-ая изотропная и 2-ая анизотропная, имеют плоскую границу раздела, которая проходит через координатную поверхность zx (рис. 2.8).
Рис. 2.8. К задаче №14 Проводимости сред равны нулю. В первой среде существует магнитное
поле H1 x0 Hx1 y0 H y1 . Определить магнитное поле во второй среде.
Параметры сред: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
, |
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||
1 0 |
|
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|
1 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
z |
|
|
|
|
|||
Решение:
Согласно рис. 2.8 и граничным условиям, записываем связь между векторами первой и второй сред:
H1 H2 Hx1 Hx2 , Hz1 Hz 2 0, ,
B1n B2n 0 H1y B2n .
Запишем вектора H и B для первой среды:
H1 x0 Hx1 y0 H y1, B1 0 H1 x0 0 Hx1 y0 0 H y1.
Запишем выражение для вектора H2 , составляющие которого надо определить из граничных условий:
H2 x0 Hx2 y0 H y 2 z0 Hz 2 .
Так как во второй среде магнитная проницаемость представлена тензором, то вектор магнитной индукции для второй среды через материальное уравнение запишем в виде произведения двух матриц и перемножим их:
|
|
|
B |
|
|
|
0 |
|
0 |
|
H |
x 2 |
|
|
0 H x 2 H y 2 |
|||||
|
|
|
x 2 |
|
|
|
|
|
|
|
H |
|
|
H |
|
|
|
|
||
|
|
B |
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||
B |
0 |
|
x 2 |
H |
y 2 |
|||||||||||||||
2 |
e2 |
|
|
|
|
|
|
|
|
y 2 |
|
|
0 |
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Bz 2 |
|
|
0 z |
|
0 |
|
|
|
|
|
|
|
|||||
В результате получим следующее выражение:
.

48
B2 x0 0 Hx2 H y 2 y0 H x2 0 H y 2x0 0 Hx1 0 H y 2 y0 H x1 0 H y 2 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Вектор B2 |
будет полностью определен, если будут определены H x 2 |
и |
||||||||||||||||||||||||||
H y 2 . Но Hx2 |
|
Hx1 |
(равенство |
|
тангенциальных |
составляющих) |
и |
|||||||||||||||||||||
составляющая By 2 Hx1 |
|
0 H y 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Приравняв составляющие (равенство нормальных компонент) |
||||||||||||||||||||||||||||
By 2 By1 , получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
By 2 Hx1 0 H y 2 B1y 0 H1y . |
|
||||||||||||||||||||||
Отсюда определим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
H |
|
|
H |
|
|
|
|
H |
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
y 2 |
y1 |
0 |
x1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зная составляющие магнитного поля второй среды, запишем |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
конечное выражение векторов H2 |
и B2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
H2 x0 H x1 |
y0 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
H y1 |
|
|
|
|
H x1 |
, |
|
||||||||||||||||
|
|
|
|
0 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
B2 x0 |
|
0 |
|
|
|
|
H x1 H y1 |
|
y0 0 H y1. |
|
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача №15
Два диэлектрика, обладающие относительными диэлектрическими проницаемостями r1 и r 2 имеют плоскую границу раздела (рис. 2.9).
Рис. 2.9. К задаче №15
Вектор E электрического поля в первой среде образует угол 1 с осью
X .
Найти вектора E и D во второй среде и угол преломления 2 .
Численный ответ привести для r1 1, r 2 4, E1 1 В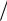 м, 1 30 .
м, 1 30 .
Решение:
49
1. Найдем вектора E и D во второй среде. Запишем для первой среды
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
общее выражение напряженности электрического поля |
|
E2 |
E2 |
|
|||||||||||||||||||||
E |
и |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
n1 |
|
||||
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
E 1 E1 sin 1 , |
|||||||||
вектора |
электрической |
индукции |
D |
E1 , |
|
|
где |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
E cos . Для второй среды – |
|
|
E2 |
E2 |
|
|
|
|
|
. |
|
|
|
|||||||||||
E |
E |
|
, |
D |
E |
|
|
|
|||||||||||||||||
n1 |
1 |
1 |
2 |
|
|
|
2 |
|
n2 |
|
2 |
|
|
2 2 |
|
|
|
|
|||||||
|
Воспользуемся граничными условиями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
E 1 E 2 , Dn1 Dn2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Тангенциальная составляющая |
напряженности |
|
электрического |
поля |
||||||||||||||||||||
второй среды легко определяется первым граничным условием ( E 1 E 2 ).
Нормальная составляющая электрического поля второй среды определяется из второго граничного условия и материального уравнения:
r1En1 r 2 En2 , откуда En2 ( r1 / r 2 )En1 .
Подставляя численные значения, получим:
E 1 E 2 E1 sin 1 0,5 В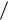 м , En1 E1 cos 1 0,87 В
м , En1 E1 cos 1 0,87 В м ,
м ,
En2 ( r1 / r 2 )En1 ( r1 / r 2 )E1 cos 1 0, 2275 В м .
м .
Величина напряженности электрического поля во второй среде равна
E2 
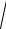 0,52 0, 222 0,546 В
0,52 0, 222 0,546 В м , тогда
м , тогда
D2 2 E2 4 0,546 2,184 Кл м2 .
м2 .
2. Найдем угол преломления 2 . Для этого составим систему уравнений
E1 sin 1 E2 sin 2 ,r1E1 cos 1 r 2 cos 2 .
Поделив первое уравнение на второе, получим r 2tg 1 r1tg 2 , которое позволяет определить угол преломления 2 :
|
|
arctg |
r1 |
tg |
66,6 . |
2 |
|
||||
|
|
r 2 |
1 |
|
|
|
|
|
|
|
Задача №16
Относительная диэлектрическая проницаемость среды изотропного диэлектрика r 4 . Чему равна электрическая восприимчивость Э ?
Решение: |
|
|
Используя |
соотношение 1 Э , получим, |
что Э 1. |
Следовательно, Э |
4 1 3 . |
|
. Задача №17
Напряженность магнитного поля в среде, обладающей r 161, H 0,1 А м . Чему равен вектор намагниченности среды M ?
м . Чему равен вектор намагниченности среды M ?

50
Решение:
Согласно (1.10), магнитная восприимчивость среды определяется какМ r 1 102 1 101, а намагниченность среды M равна
M 0 М H 4 10 7 160 0,1 126,8 10 7 Тл.
. Задача №18
Плоский воздушный конденсатор, пластины которого имеют форму дисков радиуса a , подключен к источнику переменного гармонического напряжения частоты . Диэлектрик внутри – воздух. Расстояние между дисками d . Найти энергию электрического и магнитного полей внутри конденсатора.
Решение:
Напряжение между пластинами меняется по гармоническому закону U U0 cos t . Напряженность электрического поля определим через
напряжение
|
|
|
|
|
|
|
|
E |
U |
cos t. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
Электрическая энергия равна |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
W |
|
E2 |
U 2 |
|
|
|
|
|
|
|
|
|
a2 |
U 2 cos2 t. |
|
||||||
0 |
|
V |
0 0 a2d cos2 t |
0 |
|
(2.14) |
|||||||||||||||
Э |
2 |
|
2d 2 |
|
|
|
|
|
|
|
|
|
2d |
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Магнитную энергию определим по формуле: |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
WМ |
|
H 2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0 |
2 |
dV . |
|
|
|
|
|
(2.15) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
Напряжённость магнитного поля определим из закона полного тока |
|||||||||||||||||||||
(2.1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
r U |
|
|||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
СHdl |
H 2 r t |
|
|
dS |
|
r2 0 |
t , H |
0 |
|
sin t. |
|||||||||||
|
|
|
2d |
||||||||||||||||||
L |
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив значение напряжённости магнитного поля в (2.14), получим:
0
2
W 0 0 U0
М 2 2d
|
|
U |
|
2 |
а4 2 d |
|
0 |
2d |
0 |
|
4 |
|
|
|
|
2 |
|
|
|
|
a 2 |
|
|
|
|
|
|
|
|
sin2 t d |
r3dr d ) |
|
|
|
|||||||
|
|
|
|
|
|
0 0 |
|
|
|
|
|
(2.16) |
|
|
|
|
|
0 |
02 2 U0 a2 |
2 |
|
||||
|
|
2 |
t |
1 |
2 |
t. |
||||||
sin |
|
|
|
|
|
|
sin |
|
||||
|
2 |
|
4d |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Задача №19
Докажите, что вектор E , представленный выражением E y0 Ey0 cos t kz , является решением волнового уравнения.
