Квантовая и оптическая электроника

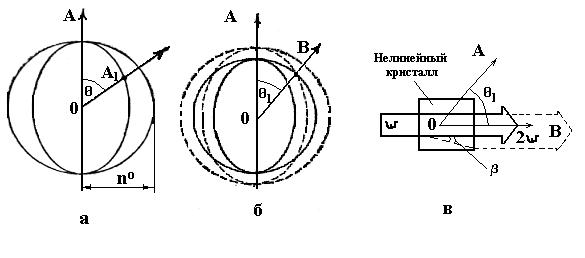
191

Плоскость, проходящую через оптическую ось и направление распространения световой волны, называют плоскостью главного сечения. Особенности распространения света внутри кристалла состоят в том, что световая волна, попадая в кристалл, превращается в две волны, характеризующиеся разными скоростями и поляризациями. Одну из этих волн принято называть обыкновенной, а другую — необыкновенной. Первая поляризована перпендикулярно к плоскости главного сечения, а вторая поляризована в этой плоскости. Световые лучи, проходящие сквозь кристаллы не отклоняясь, соответствуют обыкновенной световой волне, а отклоняющиеся световые лучи — необыкновенной волне.

Показатель преломления для обыкновенной волны не зависит от направления ее распространения в кристалле. Будем обозначать этот показатель преломления через no. Что же касается необыкновенной световой волны, то ее показатель преломления зависит от угла θ между направлением распространения волны и оптической осью кристалла nе(θ).

Приведем график зависимости пе от угла; эта зависимость изображается в виде эллипса, показанного на рис. 8,1, а. Здесь ОА — оптическая ось кристалла, длина отрезка ОА1 есть значение функции nе(θ) от угла θ между ОА и ОА1.

Рис. 8.1

На том же рисунке изображена окружность радиуса no (для обыкновенной волны). Из рисунка видно, что в направлении оптической оси (когда no = 0) показатели преломления обыкновенной и необыкновенной волн, а значит, и (скорости) указанных

192

волн различаются наиболее сильно.

Теперь вернемся к вопросу об удвоении частоты света. На рис. 8.1, б показаны сплошными линиями кривые для показателей преломления обыкновенной и необыкновенной волн некоторой частоты ω. На том же рисунке штриховыми линиями показаны соответствующие кривые для волн частоты 2ω. Как и следовало ожидать, с увеличением частоты света показатель преломления растет. Можно, однако, видеть, что существуют направления,— например направление ОВ, — вдоль которых выполняется равенство: nωo = n2e ω (θ1 ) . Напомним, что именно это условие требуется

для того, чтобы происходила передача энергии от исходной световой волны частоты ω к переизлученной световой волне частоты 2ω. Рассматриваемое условие называют условием волнового синхронизма. Соответственно говорят о направлении ОВ как о направлении синхронизма, а об угле θ1 (угле между направлением синхронизма и оптической осью кристалла) как об угле синхронизма. Итак, в направлении синхронизма показатель преломления для обыкновенной световой волны частоты ω равен показателю преломления для необыкновенной волны частоты 2ω.

После сделанных замечаний нетрудно сообразить, как можно практически осуществить удвоение частоты лазерного излучения. Для этого надо взять подходящий кристалл и вырезать образец таким образом, чтобы падающий на него нормально лазерный луч частоты ω образовывал угол синхронизма θ1 с оптической осью кристалла ОА (рис. 8.1, в). Надо также позаботиться о поляризации исходного лазерного пучка: он должен быть поляризован перпендикулярно плоскости главного сечения (перпендикулярно к плоскости рисунка) — с тем, чтобы сыграть в кристалле роль обыкновенной световой волны. Благодаря нелинейности поляризации в кристалле возникнет световая волна частоты 2ω, поляризованная в плоскости главного сечения. Световой пучок частоты 2ω показан на рис. 8.1, в штриховыми линиями. Двойное лучепреломление приводит к сносу этого пучка в поперечном направлении; снос характеризуется углом β. Снос отсутствует (β=0), когда угол синхронизма равен 90°.

193

Сейчас уже освоили производство различных типов удвоителей оптических частот, позволяющих преобразовывать во вторую гармонику до 30–50% мощности исходного светового пучка. Применяется также термин «генерация оптических гармоник»: второй гармоники, третьей, четвертой и т.д. — в зависимости от того, во сколько раз умножается частота исходного лазерного излучения. Эти преобразователи используют в лазерах на гранате с неодимом. В качестве кристаллов с нелинейной поляризацией применяют кристаллы дигидрофосфата калия (КН2РО4), называемые условно кристаллами KDP, ниобата лития (LiNbOo), ниобата бария-натрия (Ba2NaNb5OL5) и др. Их обычно называют нелинейными кристаллами.

Умножение оптических частот возможно лишь тогда, когда используется лазерное излучение. Здесь принципиально важна когерентность излучения. Ведь только благодаря высокой когерентности излучения лазеров можно достаточно сильно сконцентрировать световую мощность в каком-то определенном направлении в пространстве и притом в очень узком интервале частот. В связи с этим важно обратить внимание на то, что условие синхронизма относится всякий раз к определенной частоте света и к определенным направлениям распространения света в данном кристалле. Если, например, изменится частота исходного лазерного пучка, то изменится и угол синхронизма; иначе говоря, станут другими направления синхронизма. Поэтому очень важно, чтобы световой пучок был не только интенсивным, но и при этом остронаправ-

ленным и монохроматическим.

Взаимодействие волн с нелинейной средой. Преобразова-

ние частоты лазерного излучения может быть осуществлено при вынужденном излучении среды с инверсной населенностью уровней, возникающем при лазерной накачке. При этом возможно лишь уменьшение частоты преобразованного излучения. Преобразователи частоты, работающие по такому принципу, относятся к лазерным генераторам с лазерной накачкой. Возможно также преобразование частоты, подчиняющееся законам нелинейной оптики.

Плотность мощности лазерного излучения может быть настолько велика, что в среде индуцируются переходы, относящиеся к нелинейным эффектам. Спектр отклика нелинейной системы

194

всегда шире спектра возмущения, поэтому при нелинейном взаимодействии лазерного излучения со средой могут наблюдаться процессы преобразования частоты лазерного излучения.

При определенных условиях преобразованное по частоте лазерное излучение может усиливаться, распространяясь в нелинейной среде. На основе таких процессов возможно создание усилителей и генераторов на новых оптических частотах.

При линейном воздействии электромагнитного поля на атом среды в нем под действием электромагнитного поля индуцируется электрический дипольный момент (d), пропорциональный напряженности электрического поля d = χE(t) , где c — поляризуемость атома.

При нелинейном взаимодействии поля и среды поляризацию среды необходимо рассчитывать с учетом нелинейного отклика на внешнее электромагнитное поле. Нелинейный отклик поляризации можно аппроксимировать степенным рядом:

где aij, bikj, cijkL — тензоры линейной, квадратичной и кубической поляризуемости среды; i, j, k, L = x, y, z. Эти уравнения даны для анизотропной среды, в которой каждая составляющая напряженности электрического поля Еj вызывает поляризацию во всех трех направлениях осей системы. В разложении поляризации среды (8.1) могут быть учтены и члены более высоких порядков. Подставляя (8.1) в уравнение для поля

где линейная поляризация среды характеризуется абсолютной проницаемостью ε а, а квадратичная — последним слагаемым в

(8.2).

В дальнейшем ограничимся рассмотрением одномерного случая, когда ∂∂x = ∂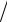∂y = 0 , и взаимодействием трех частот, для которых ω1+ω2 = ω3.

195

Подставив в уравнение (8.2) значения для Р, выполним дифференцирование, предполагая, что напряженность электрического

поля медленно меняется с расстоянием z, т.е. dE k >> d 2 E , и учи- dz dz2

тывая, что уравнение (8.2) решается для каждой частотной компоненты отдельно получим

Это исходные укороченные уравнения для амплитуд трех взаимодействующих волн с частотами, подчиняющимися соотношению ω1+ω2=ω3. Каждое уравнение описывает изменение напряженности поля с расстоянием z на одной из частот в зависимости от напряженности электрического поля на двух других, а также от разности фаз между полем и поляризацией.

Определим изменение энергии излучения в процессе распространения и взаимодействия полей. Введем некоторые упрощения. Будем считать, что среда изотропна, немагнитна, не обладает потерями: σ1 = σ2 = σ3 = 0, кроме того, k3 = k1 + k2.

Сделав некоторые преобразования в (8.3)–(8.5), найдем

где j = ne0c E ( z ) 2 / 2.

Проанализировав соотношение (8.6), можно сделать следующие выводы: 1)увеличение интенсивности на суммарной частоте ω1 + ω2 = ω3 может происходить только за счет уменьшения интенсивности на других двух частотах; 2) увеличение интенсивности на одной из частот ω1 или ω2 обязательно сопровождается одновременным ростом интенсивности на другой частоте ω2 или ω1 за счет падения интенсивности на частоте ω3. Таким образом, в нелинейной квадратично поляризуемой среде возможно усиление

196

суммарной частоты ω3, когда имеется мощное излучение накачки на частотах ω1 и ω2 и усиление разностных частот ω1 и ω2, когда присутствует мощное излучение накачки на суммарной частоте ω3.

На рис. 8.2, а, б приведены схемы преобразования частоты ω в частоту второй гармоники 2 ω и зависимости интенсивности излучения J от длины нелинейной среды L. На рисунке введены обозначения 1 — лазер накачки; 2 — нелинейная среда.

Рис. 8.2

Внутрирезонаторное преобразование частоты ω в частоту второй гармоники 2 ω осуществляется для повышения КПД преобразования.

Помещая нелинейную среду в резонатор лазера (рис. 8.2, в), где она находится в более мощном поле, чем на выходе лазера, можно обеспечить выходное излучение лазера только на частоте второй гармоники. Для этого в резонаторе с зеркалами, непрозрачными для излучения на основной частоте ω, необходимо установить нелинейную среду с коэффициентом преобразования, обес-

печивающим оптимальную связь с выходом.

Преобразование основной частоты ω в частоту высших гармоник. Такое преобразование основного излучения может производиться последовательно, когда излучение на удвоенной частоте лазерного излучения снова удваивается в среде с квадратичной нелинейностью. Таким образом, возможно получение четных гармоник основного излучения.

197

Использование нелинейных сред с кубической поляризацией [третий член в разложении (8.1)] позволяет получать поляризацию с утроенной частотой

при распространении мощного лазерного излучения на частоте ω. Поляризация на утроенной частоте является источником излучения на частоте 3 ω, как это следует из уравнений Максвелла. При условии фазового пространственного синхронизма [kj(3ω) = kj(ω) + + kk(ω) + ki(ω)] фазовые скорости распространения волн основной и утроенной частот равны: происходит эффективное когерентное преобразование основной частоты в частоту третьей гармоники.

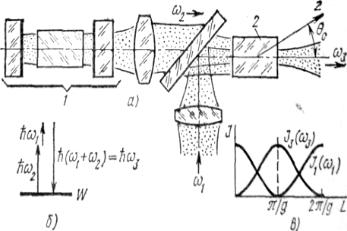
8.3 Параметрическое преобразование частоты

Схемы параметрического преобразования частоты ω2 показаны на рис. 8.3, а, б, где введены обозначения: 1 — лазер накачки; 2 — нелинейная среда. Зависимость интенсивности поля J от длины нелинейной среды L изображена на рис. 8.3, в. Параметрическое преобразование частоты является частным случаем трехволнового взаимодействия, при котopoм ω1+ω2 = ω3. Если частота излучения лазера накачки ω2 = ω3 – ω1, то для соблюдения закона сохранения энергии необходимо вспомогательное излучение с частотой ω1 (для суммирования частот), т.е. увеличения частоты излучения лазера накачки до ω3. Увеличение энергии на частоте ω3 по мере распространения в нелинейной среде вызывает, согласно

198

частотами ω2 и ω1.

Будем считать, что энергия излучения накачки велика и взаимодействие излучений не оказывает на нее влияния, т.е. dE2/dz=0. При этом должно выполняться условие фазового синхронизма k = 0. Из уравнений (8.3)–(8.5) в отсутствие поглощения σL = σ2 = σ3 = 0 найдем

Данные соотношения показывают, что энергия излучения на частоте ω1 полностью переходит в энергию излучения на частоте

Если нелинейная среда обладает длиной L > Lкр, то энергия излучения ω1 периодически преобразуется в энергию излучения с частотой ω3, и наоборот. Параметрическое преобразование частоты, таким образом, эффективно, если L = Lкр.

Параметрическое трехволновое взаимодействие, отличающееся от рассмотренного в разделе 8.3, имеет место, когда частота мощного излучения лазера накачки ω1+ ω2 = ω3. В этом случае параметрическое преобразование сводится к усилению разностной частоты. Слабые сигналы на частотах ω1 и ω2 взаимодействуют в нелинейной среде с мощной волной накачки на частоте ω3 и усиливаются. Если нелинейная среда помещена в резонатор, настроенный на частоту слабого сигнала, то система работает как параметрический резонаторный усилитель. Если потери в резонаторе могут быть скомпенсированы усилением, то усилитель с нелинейной средой самовозбуждается. Параметрический генератор может работать на любой из низкочастотных волн или излучать

199

обе волны одновременно, если система имеет двухволновой

резонатор и условия самовозбуждения выполнены для обеих волн.

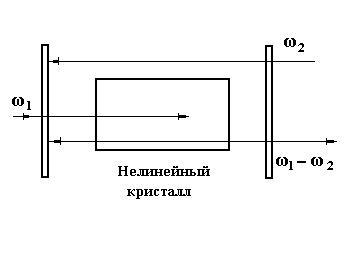
Параметрический усилитель. Такой усилитель (рис. 8.4, а,

здесь: 1 — лазер накачки; 2 — нелинейная среда) представляет собой анизотропную нелинейную среду, в которой выполнены условия фазового синхронизма: k = k3 − (k1 + k2 ) = 0 , причем среда

прозрачна для частот ω1, ω2, ω3. Если предположить, что изменением энергии лазера накачки можно пренебречь (dE3/dz = 0), то уравнения (8.3)–(8.5) с учетом обозначений, аналогичных (8.8), примут вид

где

βп = 0,5[ω1ω2 / ε] b E3 .

Рис. 8.4

При больших значениях βпz интенсивность растет экспоненциально еβпz.

200

Параметрический генератор. Существуют различные оп-

тические схемы параметрических генераторов света. Схема, показывающая принципиальную работу генератора, дана на рис. 8.5 (устройство для поворачивания нелинейного кристалла здесь не показано).

Схема не требует особых пояснений. Заметим только, что оба зеркала резонатора прозрачны на частоте волны накачки. Для более низких частот левое зеркало является полностью от-

прозрачностью. В данной схеме генерируются одновременно обе световые волны — как на частоте ω2, так и на частоте ω1– ω2. Используются также схемы, где генерируется только одна из этих волн; для другой волны специально создаются высокие потери, приводящие к срыву ее генерации.

Как уже отмечалось, при взаимодействии световых волн на частотах ω1 и ω2 в среде с нелинейной поляризацией может появиться световая волна на разностной частоте ω1 – ω2.

Поместим нелинейный кристалл между двумя зеркалами, образующими оптический резонатор. Ориентируем кристалл внутри резонатора так, чтобы направление синхронизма (для частот ω2 и ω1 – ω2 совпадало с осью резонатора. Введем в такой резонатор вдоль его оси когерентную волну на частоте ω1, так называемую волну накачки. Эта световая волна должна быть достаточно интенсивной, чтобы могла проявиться нелинейность поляризации кристалла. Кроме того, в соответствии с условием синхронизма волна накачки должна быть определенным образом поляризована. Если все эти требования выполнены, в нелинейном кристалле будут происходить процессы, которые можно представить следующим образом. Мощная волна накачки на частоте ω1 взаимодействует со слабым сигналом частоты ω2, который неизбежно присутствует в шуме, связанном с различными самопроизвольными пе-