Квантовая и оптическая электроника

211

Однако в те годы не приходилось рассчитывать на развертывание подобных исследований, поскольку отсутствовали источники мощного когерентного свет. Несмотря на это, С.И. Вавилов много размышлял о возможных исследованиях нелинейных явлений в оптике. Его исключительная научная интуиция, умение видеть на много лет вперед в полной мере проявились в монографии «Микроструктура света», вышедшей в 1951 г. В этой монографии были удивительно полно сформулированы основные задачи и намечены принципиальные пути развития нового направления в оптике. С.И. Вавилов дал этому направлению название нелинейная оптика.

9. ТРАНСФОРМАЦИЯ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ

Основные теоретические сведения

Формирование заданного набора мод во многом определяется оптическими компонентами, входящими в состав устройств формирования и трансформации лазерного излучения. В качестве оптических компонентов могут быть применены зеркала разной кривизны, призмы, диафрагмы и другие более сложные структуры. Лазерный пучок преобразуют в процессе формирования или в свободном пространстве, пропуская через соответствующую оптическую систему. Поскольку при этом происходит изменение пространственного распределения пучка (т.е. пучок может быть сфокусирован или расширен), такое преобразование называют

пространственным. Другой способ преобразования, с которым также довольно часто приходится сталкиваться, имеет место, когда пучок пропускают через усилитель или цепочку усилителей. Такое преобразование будем называть амплитудным, т.е. главный эффект здесь состоит в изменении амплитуды пучка. Встречается также третий, менее тривиальный случай, когда в результате прохождения пучка через соответствующую нелинейную оптическую среду изменяется длина волны пучка (преобразование длины волны). Наконец, с помощью подходящего электрооптического или нелинейного элемента можно изменить форму выходного импульса лазера. Последний случай назовём временным преобразованием. Следует отметить, что во многих случаях все эти четыре типа преобразования оказываются взаимосвязанными.

∙где p и l — радиальный угловой индексы моды; r и ϕ — текущие полярные координаты в сечении пучка; а — радиус сече-

ния резонатора; N — число Френеля; Jp — функция Бесселя p-го порядка; vp(l+1)– (l+1)- й корень функции Бесселя p-го порядка.

∙Рассмотрим подробнее распределение интенсивности излучения для резонатора, составленного из сферических зеркал.

∙Общее выражение, которое описывает нормированное распределение интенсивности в пятне для данной моды при прямоугольном сечении резонатора, имеет следующий вид:

где x и y — текущие прямоугольные координаты в сечении пучка; ω — параметр, характеризующий масштаб распределения интенсивности (расстояние от оси пучка до той точки, где интенсивность в сечении основной моды уменьшается в е2 раз); Hm и Hn — полиномы Эрмита порядка, соответствующего индексу поперечной моды.

Для типов низших порядков полиномы Эрмита таковы:

Н0(ξ) = 1,

Н1(ξ) = 2ξ, (9.4) Н2(ξ) = 4ξ2 – 2, Н3(ξ) = 8ξ2 – 12.

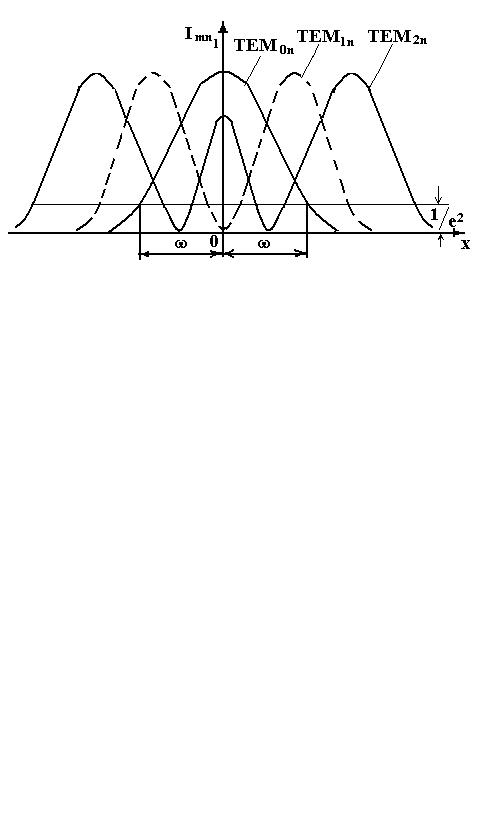
Распределения интенсивности излучения, соответствующие низшим модам, показаны на рис. 9.1. Основная мода ТЕМ00 имеет распределение, описываемое функцией Гаусса, симметрично расположенной относительно начала координат. Для последующих мод характерно более сложное распределение с симметричным чередованием максимумов и нулевых минимумов. Число минимумов в распределении равно соответствующему индексу моды, а число максимумов — на единицу больше. Периферийные максимумы распределения больше центральных.

214

Масштаб распределения как в случае прямоугольной, так и в случае цилиндрической симметрии резонатора определяется параметром ω. Величина ω равна расстоянию от оси пучка до той

Рис. 9.1

точки, где интенсивность в сечении основной моды уменьшается в е2 раз (амплитуда — в е раз).

При использовании лазеров в бытовой радиоаппаратуре важное практическое значение имеет размер пятна лазерного пучка на зеркале резонатора, либо на определённом расстоянии от выходного зеркала, поэтому рассмотрим пространственное преобразование пучка. Ограничимся рассмотрением распространения гаус-

216

где z — текущая координата вдоль оси пучка, отсчитываемая от перетяжки.

Из формулы (9.11) следует, что зависимость

( ω ω0 ) = f (2z Rэ)

является универсальной для любого резонатора. Следует помнить, что величина ω (z) дает действительный результат пятна (уменьшение интенсивности в е2 раз) только для основной моды. Моды высших порядков имеют больший радиус пятна, который может быть найден из выражения (9.1) и (9.2).

Например, индексам 1 и 2 при прямоугольной симметрии резонатора соответствует радиус пятна 1,49ω и 1,73ω соответственно. Каждый размер соответствует данному индексу моды. Если мода имеет два различных индекса, то и размер пятна в обоих измерениях разный.

С увеличением расстояния до перетяжки размер пятна увеличивается. При z >> Rэ, как видно из формулы (9.11), размер пятна возрастает линейно, что позволяет ввести угол расхождения пучка ОКГ как предел отношения ω/z при координате z, стремящейся к бесконечности:

Величина θ определяет угол расхождения пучка основной моды в одну сторону от оси, отмечаемый по уровню уменьшения интенсивности в е2 раз. Моды высших порядков характеризуются большими углами расхождения. Возрастание угла расхождения с увеличением индекса моды соответствует увеличению размера пятна.

220

визны R2 выходящей волны. Радиус кривизны R2 будет определяться формулой (9.21). Следовательно, мы имеем как амплитудное (с помощью формулы (9.22)), так и фазовое (с помощью (9.23)) распределения поля волны на выходе линзы. Эта волна имеет гауссово распределение по амплитуде и сферический волновой фронт, т.е. гауссов пучок остаётся таковым же и после того, как он пройдёт через систему тонких линз. Этот результат остаётся верным и в случае прохождения пучка через систему толстых линз (рассматривая её как совокупность тонких линз). Зная размер пятна и радиус кривизны после линзы, можно вычислить соответствующие величины в любой точке пространства. Например, размер пятна ω02 в новой перетяжке пучка и расстояние L2 от линзы до этой перетяжки по формулам (9.20, 9.21) в обратном порядке:

плюс, либо минус. Выражения (9.24) весьма полезны при решении различных задач, связанных с распространением гауссова пучка.

Замечание: если первая перетяжка совпадает с первой фокальной плоскостью (L1=f), то вторая перетяжка совпадает со второй фокальной плоскостью линзы (L2=f). Однако в общем случае плоскости обеих перетяжек не связаны соотношением геометри-

ческой оптики (т.е. 1 + 1 ¹ 1 ).

L1 L2 f

Наличие линзы (роль линзы могут сыграть подложки сферических зеркал) на пути распространения излучения ОКГ может существенно изменить характеристики пучка за линзой; при этом линза не влияет на модовую структуру пучка, а изменяет размер пятна и радиус кривизны волнового фронта.

Линза с фокусом f преобразует пучок так, что выполняются следующие соотношения: