Математика для гуманитарных, экологических и экономико-юридических специальностей. Часть 1

3 1

1.14.Гипотеза континуума

Â1878 г. Г. Кантор высказал предположение о том, что всякое множество действительных чисел либо конечно, либо счетно, либо несчетно (т.е. эквивалентно множеству всех действительных чисел). Оставим в стороне конечные множества, тогда по Г. Кантору всякое бесконечное десятичное число принадлежит либо счетному множеству N, либо несчетному множеству M с кардинальным числом

M = 1 = 2N = 2 0.

Несчетное множество M с большей мощностью получено по ана-

логии с конечными множествами путем нахождения булеана счетного множества N. Очень уж непохожи свойства конечных и бесконеч-

ных множеств, поэтому вполне естественно задать вопрос: верно ли, что мощность множества всех подмножеств счетного множества есть первая мощность, превосходящая мощность множества всех натуральных чисел? Это и есть знаменитая гипотеза континуума.

Несмотря на простоту формулировки, эта гипотеза десятки лет оставалась удивительно неподатливой, хотя над ней работали луч- шие математики мира. В 1900 г. на втором Международном конгрессе в Париже немецкий математик профессор Геттингенского университета Давид Гильберт (1862–1943) опубликовал обращение к математикам мира, в котором сформулировал более двух десятков наиболее важных и не решенных в то время проблем. В этом списке проблему (гипотезу) континуума Д. Гильберт поставил на первое место. До 30-х годов прошлого столетия все попытки решить первую проблему Гильберта оканчивались нулевым результатом. Лишь в 1938 г. Курт Гедель (1906–1978) — австрийский логик и математик — показал, что континуум гипотеза не может быть опровергнута традиционными средствами теории множеств.

Более существенный результат получил в 1966 г. профессор Станфордского университета (США, штат Иллинойс) П. Коэн. Он доказал независимость гипотезы континуума от других аксиом теории множеств. Согласно его выводам можно считать, что между счетным множеством и множеством всех его подмножеств существует промежуточное множество, но можно считать, что его не существует.

Âлюбом случае это не противоречит всем остальным аксиомам теории множеств. Здесь можно провести аналогию с пятым постулатом о параллельных прямых. Его можно принять, можно и отвергнуть.

Âлюбом случае он не противоречит всем остальным аксиомам геометрии.

Следует отметить, что не все математики одинаково формулируют гипотезу континуума. Например, согласно [29, с. 52] гипотезой континуума называют утверждение

3 3

отрезка [0; 1) эквивалентно множеству всех действительных чисел в интервале 0 ≤ x < 1.

Пусть даны два отрезка AB è CD различной длины. Эквивалент-

ны ли множества их точек? Интуиция нам подсказывает, что в отрезке длиной, равной, например, одному сантиметру, содержится гораздо меньше точек по сравнению с отрезком, допустим, метровой длины. Кантор предложил очень остроумный способ доказательства того, что между точками отрезков различной длины существует взаимно одно-

не совпадает с точкой a, то не совпадают и точки b′ è a′. Таким способом любой точке отрезка AB можно однозначно поставить в соответствие точку отрезка CD и наоборот: всякой точке отрезка CD однозначно соответствует точка отрезка AB. Следовательно, множества точек отрезков AB è CD эквивалентны, а это значит, что (говоря

языком конечных множеств) число точек на отрезке, равном расстоянию от Земли до Солнца, точно такое же, что и на отрезке, равном, например, радиусу атомного ядра. Подобным образом Г. Кантор доказал, что множество точек конечного отрезка AB и множество точек

всей числовой оси эквивалентны.

Следующий результат Г. Кантора является еще более удивительным. Он доказал, что множество точек отрезка эквивалентно множеству точек квадрата, сторона которого равна этому отрезку. Вооб- ще-то Г. Кантор искал доказательство того, что мощность множества точек квадрата не эквивалентна множеству точек отрезка, и когда нашел доказательство прямо противоположного утверждения, то был настолько изумлен своим открытием, что в письме математику Р. Дедекинду писал: «Я вижу это, но не верю этому».

Принцип доказательства Г. Кантора состоит в следующем. Проведем оси декартовых координат x è y и отложим на обеих координа-

тах отрезки [0; 1). Тогда каждая точка квадрата может быть представлена двумя бесконечными десятичными дробями:

xA = 0,a1a2a3a4...; yA = 0,b1b2b3b4...

Образуем на их основе новую дробь, вставив цифры числа yA между цифрами числа xA: VA = 0,a1b1a2b2a3b3a4b4...

3 4

Очевидно, что число VA принадлежит отрезку [0; 1).

Рассмотренным способом каждой точке квадрата можно поставить в однозначное соответствие определенную точку отрезка [0; 1). Если же взять какую-нибудь точку отрезка, то, представив соответствующую ей десятичную дробь в виде чисел xA è yA, мы найдем

точку квадрата, находящуюся в однозначном соответствии с заданной точкой отрезка.

Таким образом, множество точек отрезка [0; 1) эквивалентно множеству точек квадрата, сторона которого совпадает с заданным отрезком.

Пользуясь приемом Г. Кантора, нетрудно убедиться в следующем: а) множество точек любого конечного отрезка эквивалентно множеству точек куба, ребро которого равно данному отрезку. Для доказательства этого достаточно к числам xA è yA добавить число zA (третья координата) и так же, как и в случае квадрата, найти число VA,

принадлежащее отрезку [0; 1). Аналогичное утверждение справедливо и для четырехмерного пространства, и вообще n-мерного;

б) множество точек отрезка длиной в 1 микрон эквивалентно множеству точек куба, длина ребра которого равна расстоянию от Земли до Полярной звезды (сначала множество точек микронного отрезка отобразим на ребро куба, а после этого — на весь куб);

в) множество точек микронного отрезка эквивалентно множеству точек не только трехмерного бесконечного мирового пространства (Вселенной), но и многомерного.

Подобных утверждений можно доказать сколько угодно.

1.17. Числовые множества

Как уже отмечалось, элементами множества могут быть любые объекты, числовые и нечисловые. Здесь же мы ограничимся классом числовых множеств.

Прежде всего выделим множество R всех действительных чисел.

Действительным числом называется всякая десятичная дробь. Множество R содержит положительные и отрицательные, десятичные

и обыкновенные дроби и все целые числа, поскольку любое целое число можно представить в виде десятичной дроби, если правее запятой записывать только нули.

Подмножествами множества R являются:

N = {1,2,3, 4,...} — множество натуральных чисел;

Z = {..., −3, −2, −1,0,1,2,3,...} — множество всех целых чисел;

Q — множество рациональных чисел (лат. rationalis — разум-

ный, целесообразный, обоснованный). В него входят все периодиче-

3 5

ские десятичные дроби. Любое рациональное число можно представить как отношение двух целых чисел m/n, ãäå n ≠ 0.

Все числа, не являющиеся рациональными, называются иррациональными (лат. irrationalis — неразумный), например

π3, 31, ln17, e3, e13

и так далее, поскольку ни одно из них невозможно представить в виде обыкновенной дроби, у которой и числитель и знаменатель — целые числа, положительные или отрицательные.

Геометрически действительные числа удобно представлять точ- ками числовой оси, если выбрать единицу масштаба. Расставим на числовой оси точки, например, так, чтобы расстояние между любыми соседними точками было равно 1 сантиметру. Одну точку примем за начало координат. Это точка номер 0. Пронумеруем точки справа от нуля. Получим множество N. Пронумеруем точки слева от нуля.

Это будут те же номера, но со знаками минус, то есть получим отрицательные числа. Все номера, положительные и отрицательные, вместе с числом 0 образуют множество Z. Остальным точкам числовой

оси соответствуют десятичные дроби, у которых справа от запятой имеется хотя бы одна цифра, отличная от нуля. При таком моделировании действительных чисел имеет место взаимно однозначное соответствие между множеством R и множеством всех точек числовой

îñè.

В дальнейшем будут использоваться следующие типы числовых множеств:

а) множество Õ чисел, удовлетворяющих неравенству a ≤ x ≤ b, ãäå x R,

которое называется закрытым интервалом (сегментом, отрезком) и обозначается [à, b], ãäå à è b — границы отрезка, квадратные скобки говорят о том, что à, b Õ;

б) множество Õ чисел, удовлетворяющих неравенству

a ≤ x < b,

которое называется полуинтервалом (полуоткрытым интервалом) и обозначается [à, b), круглая скобка говорит о том, что b Õ;

в) множество Õ чисел, удовлетворяющих неравенству

a < x ≤ b,

также полуинтервал, обозначается (à, b], где круглая скобка говорит о том, что à Õ;

г) множество Õ чисел, удовлетворяющих неравенству

a < x < b,

что обозначает открытый интервал.

Кроме этих четырех типов множеств будем рассматривать ограниченные и неограниченные числовые множества. Пусть множество

3 6

ÀR задано отрезком [à, b] на числовой оси. Выберем на той же оси, но вне этого отрезка точку ñ. Åñëè b ≤ ñ, то число ñ называется верхней границей множества À. Åñëè ñ ≤ à, то число ñ называется нижней границей множества À. Очевидно, что обе границы определены

неоднозначно. Для устранения неоднозначности введены понятия точ- ной верхней границы и точной нижней границы.

Наименьшая из всех верхних границ множества À называется точной верхней границей и обозначается sup A, читается: супремум

À(ëàò. supremus — высший). Наибольшая из нижних границ множества À называется точной нижней границей и обозначается inf A, читается: инфимум À (ëàò. infimum — наинизшее).

Для обозначения неограниченных числовых множеств дополним R знаками ∞, +∞, −∞.

Если множество À не ограничено сверху, то полагают sup A = +∞.

Если же оно не ограничено снизу, то принимают inf A = −∞.

Символ ∞ (без знаков) используют в тех случаях, когда множе-

ство не ограничено ни сверху, ни снизу.

С символами ∞, +∞, −∞ нельзя обращаться как с числами. Ариф-

метические операции над ними определены следующими соотношениями (à R):

a ± (+∞) = ±∞; a + (−∞) = −∞; a − (+∞) = −∞;

a (+∞) = −∞ ïðè à < 0;

(+∞) (+∞) = +∞; (−∞) (+∞) = −∞; (−∞) (−∞) = +∞;

∞a = ∞; ∞ ∞ = ∞; a(+∞) = a(−∞) = 0.

Операции (±∞) − (±∞); (±∞)(±∞); 0 (±∞) не определены.

Символами +∞ è −∞ обозначают неограниченные промежутки. Если õ R, òî

[à, +∞) = {õ | õ ≥ à}; (à, +∞) = {õ | õ > à}; (−∞, à] = {õ | õ ≤ à}; (−∞, à) = {õ | õ < à}; (−∞, +∞) = R.

Упражнения

1. Укажите номера верных выражений:

à) (ÈÀÔ) 1) N Q, 2) π/2 R, 3) 2π Q, 4) 0,333… Q, 5) −2 Z I N, 6) 1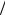3 R I Q, 7) R = Z U Q U N, 8) R = Q U Z U Q; á) (ÀÊÊ) 1) N Z, 2) −4 Q, 3) lg100 N, 4) 4 N I Z,

5) 0,81 Q I Z, 6) 14 Z I N, 7) R = NUZ U N, 8) 0 Z I N;

1.18. Множество комплексных чисел

Начнем с примера. Найдем корни уравнения x2 − 2x + 5 = 0.

Дискриминант его отрицателен. Следовательно, как известно из школьного курса алгебры, это уравнение не имеет решения, то есть не найдется ни одного действительного числа, которое в результате подстановки его вместо переменной õ обратило бы левую часть урав-

нения в нуль. Если все же найти корни уравнения по известным правилам, то получим:

x1 = 1 + 2−1; x2 = 1 − 2−1.

Нетрудно убедиться в том, что выражения õ1 è õ2 также являют-

ся корнями заданного уравнения. Для этого достаточно подставить их вместо õ и выполнить необходимые преобразования. Проверим,

например, первый корень:

(1+ 2−1)2 − 2(1+ 2−1) + 5 =1+ 4−1 − 4 − 2 − 4−1 + 5 = 0.

Тот же результат получится, если вместо õ подставить второй

корень.

Какое бы мы ни взяли квадратное уравнение с отрицательным дискриминантом, всегда будут получаться корни в виде

x1 = a + b−1, x2 = a − b−1,

ãäå à è b — некоторые действительные числа.

Итальянский математик, философ и врач Джероламо Кардано

(1506–1576) в 1545 г. предложил выражения вида a + b−1 è a − b−1

считать числами новой природы и производить действия над ними по правилам обычной алгебры. Он называл их «чисто отрицательными», «софистически отрицательными», не видел им применения

èсчитал их бесполезными, поскольку по его представлениям они не годились ни для каких измерений. В 1637 г. французский математик

èфилософ Р. Декарт ввел для них специальное название: мнимые числа. В 1777 г. Л. Эйлер предложил использовать первую букву

3 8

французского слова imaginaire (мнимый) для обозначения числа −1

(мнимая единица), то есть по Эйлеру i = −1. Благодаря немецкому математику К. Гауссу (1777–1855) символ i вошел во всеобщее упот-

ребление в математической среде [26, с. 145]. И с тех пор мнимые числа, получившие в дальнейшем название комплексных, стали записывать в виде à + bi, ãäå à è b — действительные числа. Это алгеб-

раическая форма комплексного числа.

Следует отметить, что название «мнимые числа» не очень удачно, так как слово «мнимый» обозначает «воображаемый, кажущийся». Применительно к комплексным числам такое толкование слова «мнимый» может вызвать сомнение в их существовании [11, с. 10]. На самом же деле комплексные числа являются не менее реальными, чем действительные. Однако термин «мнимые числа» прижился, давно используется в математической литературе, и нам ничего не остается, как принять к сведению, что слово «мнимый» в математике обознача- ет квадратный корень из отрицательного числа, а не «воображаемый, кажущийся».

Число à называется действительной частью комплексного числа ñ = à + bi и обозначается Re c. Число b называется мнимой частью и обозначается Im c.

Для комплексных чисел приняты следующие равенства: a + 0 i = a; 0 + b i = b i; 1 i = i; (−1) i = − i; i i = i2 = − 1.

Два комплексных числа ñ1 = à1 + b1i è ñ2 = à2 + b2i называются равными тогда и только тогда, когда à1 = à2 è b1 = b2. Åñëè õîòÿ áû

одно из этих условий не выполняется, то числа называются неравными. Выражения ñ1 ≥ ñ2 è ñ1 ≤ ñ2 не имеют смысла, то есть множество

комплексных чисел не является упорядоченным.

Если числа ñ1 è ñ2 отличаются только знаком мнимой части, то они называются комплексно-сопряженными. Например, 3 + 5i è 3 − 5i. Заметим, что в результате решения квадратного уравнения,

дискриминант которого является отрицательным, всегда получаются комплексно-сопряженные числа. Если ñ — комплексное число,

то соответствующее комплексно-сопряженное число будем обозначать символом Ò .

Сложение и вычитание комплексных чисел определено следующим образом:

c1 + c2 = (a1 + a2 ) + (b1 + b2 )i; c1 − c2 = (a1 − a2 ) + (b1 − b2 )i.

Ï ð è ì å ð 1. Åñëè ñ1 = 3 + 6i è ñ2 = 6 + 4i, òî ñ1 + ñ2 = 9 + 10i.

Умножение комплексных чисел выполняется по обычному правилу умножения многочленов с обязательной заменой i2 числом −1:

c1 c2 = (a1a2 − b1b2 ) + (a2b1 + a1b2 )i.

начала координат до точки, изображающей комплексное число (см. рис. 1.17).

Кроме алгебраической применяются и другие формы записи комплексных чисел: тригонометрическая и показательная.

Пусть ñ ≠ 0. Óãîë ϕ между осью Îõ и вектором ÎÌ (см. рис. 1.17) называют аргументом комплексного числа ñ и обозначают ϕ = Arg c.

Его величина определяется не однозначно, а с точностью до слагаемого, кратного 2π. Значение аргумента, находящееся в промежутке (−π; π], называется главным значением аргумента и обозначается аrg c, òî åñòü −π < àrg c ≤ π.

Введем обозначение Ò = r. Непосредственно из рис. 1.17 и правил тригонометрии следует, что õ = rcosϕ, ó = r i sinϕ, òî åñòü ñ = r(cosϕ + i sinϕ). Эту форму комплексного числа называют тригоно-

метрической.

Показательная форма комплексного числа имеет вид ñ = råiϕ. Таким образом, комплексное число ñ можно записывать в трех

видах:

c = a + bi = r(cos ϕ + i sin ϕ) = reiϕ.

Формула, связывающая показательную и тригонометрическую формы комплексного числа, найдена Л. Эйлером. Она имеет вид

При умножении и делении двух комплексных чисел, записанных в тригонометрической форме, можно применять следующую теорему.

Теорема. При умножении двух комплексных чисел их модули перемножаются, а аргументы суммируются. При делении двух комплексных чисел их модули делятся, а аргументы вычитаются, то есть если