
СПИНТех - Прикладная информатика / ЧМ_ЛР-5_Толстов_П-31
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное
учреждение высшего образования
Национальный исследовательский университет “МИЭТ”
Институт Системной и программной инженерии и информационных технологий
Дисциплина: Численные методы
Лабораторная работа №5
«Аппроксимация данных методом наименьших квадратов»
Вариант 21
Выполнил:
Студент П-31
Толстов Д.В.
Преподаватель:
Лавров И.В.
Москва 2022
Теория:
В общем случае рассматривают линейную по параметрам регрессионную модель вида y = b0+b1*a1(x) +…+ bk-1*a k-1(x), где a1(x), … , a k-1(x), − известные функции; b0, b1, … , bk-1 − неизвестные параметры. Пусть имеется n наблюдений (xi, yi), которые являются результатом реализации случайного вектора (X, Y). Подставим в вышеуказанную модель: y = b0+b1*a1(xi) +…+ bk-1*a k-1(xi) + εi, где i = 1, 2, … n; εi − случайные независимые друг относительно друга и распределенные по нормальному закону ошибки наблюдений. По
методу наименьших квадратов в качестве
оценок bj
принимают значения
В матричных обозначениях эту систему уравнений можно записать в виде:
|
Задание:
Написать m-файлы для реализации метода наименьших квадратов для построения линейной регрессии по x и y. Взять 10 первых точек из своего варианта. Вычислить медиану, средние значения, смещенную и несмещенную оценку среднеквадратичного отклонения, коэффициент корреляции.
x = [5:0.06:8]; Y = [1.9663 1.6476 0.7114 2.4589 3.2220 3.0810 2.9495 4.4071 ... 3.7540 4.3238 4.5238 4.5653 5.0215 4.7886 4.1480 4.4855 ... 5.1016 4.2923 4.6496 4.2193 3.9369 3.8189 3.9092 3.9575 ... 3.5582 3.8837 2.9589 2.0519 2.5481 2.3186 2.1911 2.0457 ... 2.2128 1.0942 1.3103 1.0029 0.5667 1.7896 0.4738 -0.2055 ... 1.2955 0.4975 -0.2888 0.5275 0.7079 -0.3114 0.1746 0.0137 ... -0.5175 0.6409 0.0295];
n1 = 10; x1 = x(1:n1); y1 = Y(1:n1);
x_ = 0; y_ = 0; x2_ = 0; xy_ = 0;
for i1 = 1:n1 x_ = x_ + x(i1); y_ = y_ + Y(i1); x2_ = x2_ + x(i1) * x(i1); xy_ = xy_ + x(i1) * Y(i1); end
x_ = x_ / n1; y_ = y_ / n1; x2_ = x2_ / n1; xy_ = xy_ / n1;
b0 = (x2_ * y_ - x_ * xy_) / (x2_ - x_ * x_); b1 = (xy_ - x_ * y_) / (x2_ - x_ * x_);
x_gr = x(1):0.01:x(n1); y_gr = b0 + b1 * x_gr;
plot(x_gr, y_gr, x1, y1, '*')
median_x = median(x1) median_y = median(y1) std_s = std(y1,1) %смещенная оценка среднеквадратичного отклонения std_n = std(y1,0) %несмещенная оценка среднеквадратичного отклонения cor = corrcoef(x1,y1) %коэффициент корреляции
|

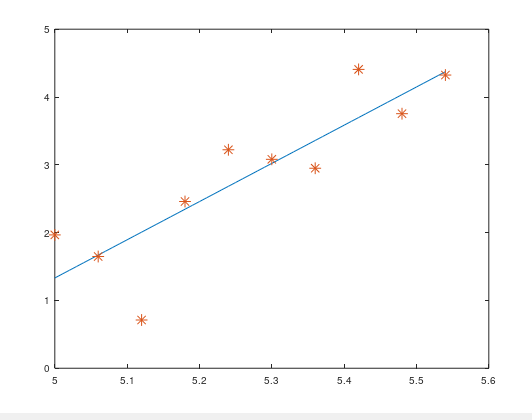
Написать m-файлы функции для реализации метода наименьших квадратов для построения нелинейной полиномиальной регрессии со степенным базисом (n = 3, 5, 7) и построить аппроксимирующие кривые.
x = [5:0.06:8]; Y = [1.9663 1.6476 0.7114 2.4589 3.2220 3.0810 2.9495 4.4071 ... 3.7540 4.3238 4.5238 4.5653 5.0215 4.7886 4.1480 4.4855 ... 5.1016 4.2923 4.6496 4.2193 3.9369 3.8189 3.9092 3.9575 ... 3.5582 3.8837 2.9589 2.0519 2.5481 2.3186 2.1911 2.0457 ... 2.2128 1.0942 1.3103 1.0029 0.5667 1.7896 0.4738 -0.2055 ... 1.2955 0.4975 -0.2888 0.5275 0.7079 -0.3114 0.1746 0.0137 ... -0.5175 0.6409 0.0295];
n = 51; y = Y';
k3 = 3; k5 = 5; k7 = 7;
Y3 = 0; Y5 = 0; Y7 = 0;
#----- k = 3 A = ones(n, k3); for i = 1:n for j = 2:k3 A(i, j) = x(i).^(j - 1); end end b_ = inv(A' * A) * A' * y; for i = 1:k3 Y3 = Y3 + b_(i)*x.^(i - 1); end
#----- k = 5 A = ones(n, k5); for i = 1:n for j = 2:k5 A(i, j) = x(i).^(j - 1); end end b_ = inv(A' * A) * A' * y; for i = 1:k5 Y5 = Y5 + b_(i)*x.^(i - 1); end
#----- k = 7 A = ones(n, k7); for i = 1:n for j = 2:k7 A(i, j) = x(i).^(j - 1); end end b_ = inv(A' * A) * A' * y; for i = 1:k7 Y7 = Y7 + b_(i)*x.^(i - 1); end
plot(x,Y3,'m',x,Y5,'r',x,Y7,'g',x,y,'.')
y=y'; figure plot(x,Y3-y,'m',x,Y5-y,'r',x,Y7-y,'g') |
Аппроксимирующие кривые и график ошибок аппроксимации:
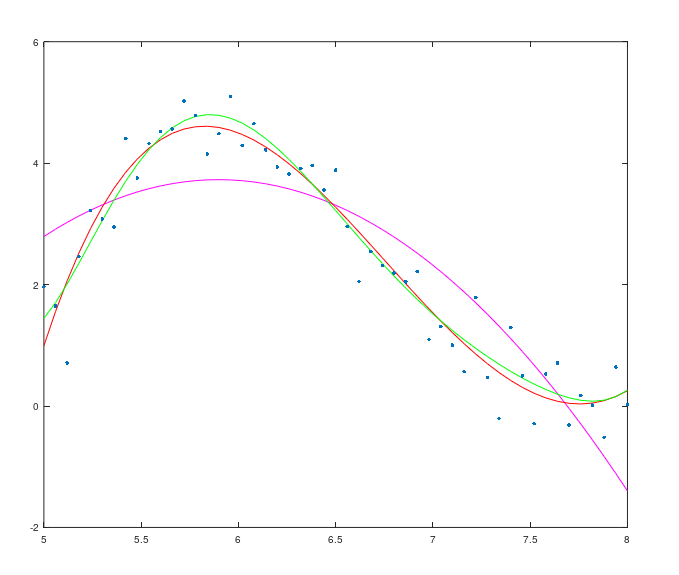

Использовать стандартные средства Matlab для построения соответствующих кривых. Сравнить результаты.
x = [5:0.06:8]; Y = [1.9663 1.6476 0.7114 2.4589 3.2220 3.0810 2.9495 4.4071 ... 3.7540 4.3238 4.5238 4.5653 5.0215 4.7886 4.1480 4.4855 ... 5.1016 4.2923 4.6496 4.2193 3.9369 3.8189 3.9092 3.9575 ... 3.5582 3.8837 2.9589 2.0519 2.5481 2.3186 2.1911 2.0457 ... 2.2128 1.0942 1.3103 1.0029 0.5667 1.7896 0.4738 -0.2055 ... 1.2955 0.4975 -0.2888 0.5275 0.7079 -0.3114 0.1746 0.0137 ... -0.5175 0.6409 0.0295];
p3 = polyfit(x, y, 3); Y3 = polyval(p3, x);
p5 = polyfit(x, y, 5); Y5 = polyval(p5, x);
p7 = polyfit(x, y, 7); Y7 = polyval(p7, x);
plot(x, Y3, 'm', x, Y5, 'r', x, Y7, 'g', x, y, '.')
figure plot(x, Y3-y, 'm', x, Y5-y, 'r', x, Y7-y, 'g') |
Аппроксимирующие кривые и график ошибок аппроксимации:
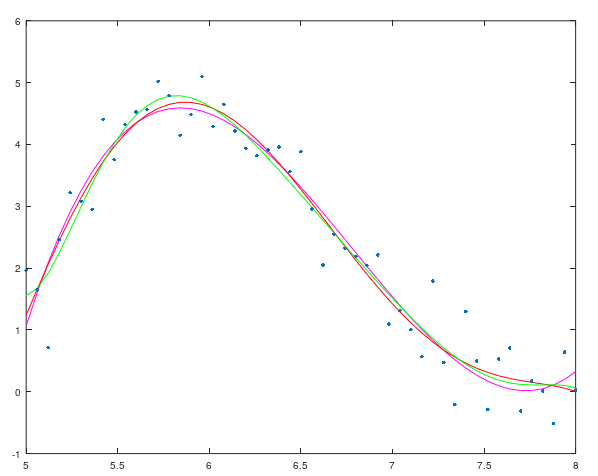
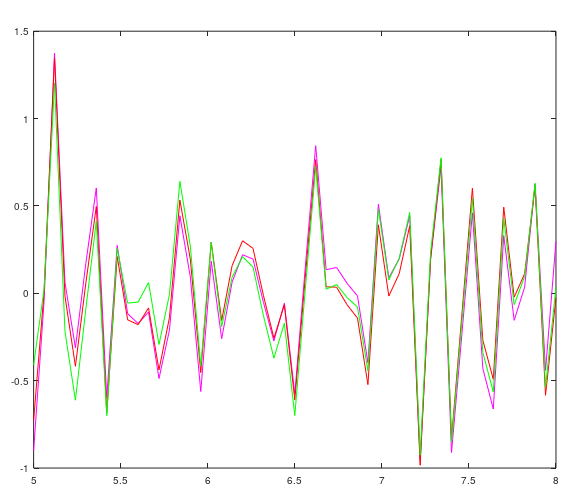
Сравнение результатов: стандартные средства Matlab решают задачу аппроксимации точнее, чем метод наименьших квадратов. С увеличением значения степенного базиса уменьшается ошибка аппроксимации и, следовательно, растет точность аппроксимирующей кривой.
Вывод: в данной лабораторной работе мы изучили методы наименьших квадратов для аппроксимации данных, приобрели навыки программирования метода наименьших квадратов для аппроксимации экспериментальных данных и использования стандартных средств системы Matlab для задачи аппроксимации.

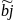 , дающие минимум функции.
, дающие минимум функции.